Тема 5. Пропускна здатність каналів зв'язку і швидкість передачі інформації

5.1 Кількість інформації

Основними характеристиками каналів зв'язку є його пропускна здатність і швидкість передачі інформації.

Перш, ніж дати визначення цим характеристикам каналу, слід встановити одиницю вимірювання кількості інформації. З цією метою прослідкуємо весь процес утворення того чи іншого повідомлення джерелом інформації.

У розпорядженні джерела інформації є певна кількість окремих повідомлень, сукупність яких називається ансамблем. Ансамбль повідомлень і відповідний йому набір кодованих сигналів відомий і на приймальній стороні. На приймальній стороні відома також ймовірність появи кожного сигналу.

Припустимо, що за допомогою телемеханічної системи можуть передаватись тільки два окремих повідомлення (наприклад, "нижче норми" і "вище норми"), яким відповідають сигнали у вигляді різнополярних імпульсів однакової ширини і висоти. Припустимо також, що обидва ці сигнали є рівноймовірні, тобто мають однакову ймовірність появи, яка дорівнює 0,5.

Приймемо за одиницю вимінювання кількості інформації нашої найпростішої системи ту кількість інформації, яку несе на собі кожен імпульс, що передасться по лінії зв'язку.

Позначимо сигнали повідомлень цифрами двійкової системи числення (одиниця і нуль): сигнал (1) передається при виборі повідомлення "нижче норми", а сигнал (0) - при виборі повідомлення "вище норми".

З введенням прийнятих позначень кожному з повідомлень, яке передасться, ставиться відповідно одна з цифр двійкової системи. При цьому кожен вибір супроводжується наступною передачею одиниці вимірювання кількості інформації.

Процес вибору повідомлень може бути проілюстрований схемою, що показана на рис.5.1. В точці а з ансамблю, повідомлень проводиться вибір між двома. рівноймовірними подіями. При цьому результат, що нас цікавить, отримується при одному виборі. Виходячи з цього, можна стверджувати, що кожен вибір одного з рівноймовірних результатів відповідає одній двійковій одиниці або одиниці кількості інформації.

Припустимо далі, що джерело інформації володіє ансамблем з m повідомлень (m>2), при чому кожному повідомленню відповідає певний стан об'єкту контролю.

Вважаючи, що події рівноймовірні, тобто

,

знайдемо ту кількість інформації, яка відповідає передачі одного повідомлення.

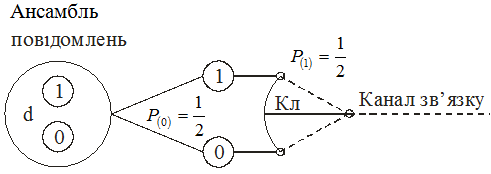
Рисунок 5.1 - Схема вибору одного з двох рівно ймовірних повідомлень

Схему вибору повідомлень для цього випадку можна представити в наступному вигляді. Загальне число повідомлень m ділиться на дві рівні групи і вибирається одна з них. Такий вибір, як уже відомо, відповідає одиниці кількості інформації. Відібрана таким група, в свою чергу, ділиться на дві рівні підгрупи, з яких вибирається одна. Очевидно і вибір цієї підгрупи пов'язаний з одиницею кількості інформації, так як він проводиться з двох рівноймовірних можливостей. Така процедура повторюється до тих пір, поки в черговій підгрупі не виявиться одного повідомлення. При цьому кількість повідомлень в групах і підгрупах може бути представлена наступним рядом чисел:

.

Останній член цього ряду, відповідно до приведеної схеми вибору повідомлень, дорівнює одиниці:

;

;

.

Логарифмуючи цю рівність, знайдемо число послідовно проведених вибірок або кількість інформації, що приходиться на одне повідомлення,

, біт (bihary digit) (5.1)

Якщо в якості основи системи логарифмів взяти число 2, то

(5.2)

або

, (5.3)

(5.3) – формула американського вченого Хартлі (1928 р.)

Кількість інформації, що припадає на одно повідомлення, дорівнює двійковому логарифму числа можливих станів об’єкту.

При кодуванні дискретних сигналів за системою двійкового комплектного коду , тому

, (5.4)

тобто кількість інформації, що відповідає передачі одного повідомлення, дорівнює числу елементів в кодованому сигналі.

В загальному випадку, коли повідомлення, що утворюють ансамбль, нерівно ймовірні, кількість інформації, яку несе на собі той чи інший сигнал повідомлення, залежить від ймовірності.

Повернемося до двохпозиційного об’єкту.

Позначимо: Р₁ – ймовірність появи повідомлення «відключено»;

Р₂ – ймовірність появи повідомлення «включено»

Сигнали, що відповідають цим повідомленням, як і раніше, позначимо цифрами 1 і 0. Будемо вести спостереження за сигналами і через строго визначені проміжки часу робити помітки про стан об’єкту. В результаті достатньо тривалого спостереження може бути складено Q послідовностей, які відрізняються одна від одної порядком чергування цифр:

(5.5)

Позначимо через N – число цифр, з яких складається кожна послідовність.

Якщо число цифр, що утворюють послідовність, велике (N), то можна рахувати, що будь – яка послідовність містить цифр 1 і цифр 0. Поява тієї чи іншої послідовності (5.5) є складною подією, що складається з простих незалежних подій типу 1 і 0. Ймовірність появи будь – якої з таких складних подій однакова і, згідно теореми про суміщення незалежних подій. Дорівнює

. (5.6)

У свою чергу, за відомою ймовірністю можна знайти і загальне число різних послідовностей Q

, (5.7)

так як

.

Визначивши, таким чином, загальну кількість послідовностей (або рівно ймовірних складних подій), знайдемо, згідно рівнянню (5.2), кількість інформації, що міститься в кожній з послідовностей:

. (5.8)

Тепер неважко знайти і середню кількість інформації, що приходиться на одне повідомлення

Рівняння (67) визначає середню кількість інформації, що приходиться на одне повідомлення, про стан двопозиційного об’єкту, коли ці повідомлення нерівно ймовірні. Для крайнього випадку, коли об’єкт завжди відключений , середня кількість інформації, яку несе на собі сигнал повідомлення, дорівнює

Очевидно, що в такому випадку необхідність у передачі повідомлень про стан об’єкта взагалі відсутня, тому що прийом диспетчером сигналу, що підтверджує відключений стан об’єкта, не змінить його освідомленності в цьому питанні.

Графік залежності величини H від ймовірності Р₁ (при цьому ), побудований за рівнянням (5.9) показаний на рис. 5.2. Видно, що величина Н досягає свого максимального значення при рівності ймовірності подій і прямує до нуля по мірі наближення до одиниці ймовірності однієї з подій.

В загальному випадку, коли контрольована величина Х може приймати m різних дискретних значень з ймовірностями Р₁, Р₂, …, Р_і, …, Р_m, рівняння (5.9) отримає вигляд:

(5.10)

де ймовірності всіх подій зв’язані між собою відношенням

Формула (5.10) визначає середню кількість інформації, що приходиться на одне дискретне повідомлення. Величина Н також характеризує степінь невизначеності подій і в теорії ймовірності має назву ентропії процесу або джерела інформації.

Ентропія (невизначеність) джерела інформації залежить від ймовірностей окремих сукупних повідомлень. Якщо повідомлення рівно ймовірні, то ентропія має максимальне значення, так як з однаковою ймовірністю може бути вибрано будь яке з них. Навпаки, при нерівності ймовірностей повідомлень невизначеність менша і в межах, коли Р₁ = 0 і Р₂=1, невизначеність стає рівною нулю.

Невизначеність (ентропія) існує тільки до отримання повідомлення з отриманням повідомлення про результат випробування вона зменшується або стає рівною нулю. При цьому чим більшою була початкова невизначеність, тим більша інформація, що отримується.

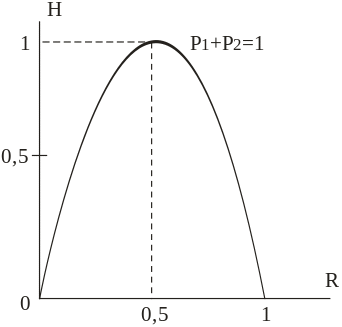
Рисунок 5.2 - Залежність ентропії від ймовірності появи однієї з подій

Задача 1. На контрольованому об’єкті є три клапани, кожен з яких може знаходитись в одному з двох положень (закритий або відкритий). З об’єкта передається інформація про зміну положення клапанів. Спостереженнями протягом тривалого відрізку часу встановлено, що з ста переданих повідомлень 70 відносяться до першого клапана, 20 до другого, 10 до третього.

Клапани працюють незалежно один від одного.

Визначити кількість інформації, яка міститься в одному повідомленні.

Розв’язок.

Позначимо:

- повідомлення про те, що перший клапан закрився;

- повідомлення про те, що перший клапан відкрився;

- повідомлення про те, що другий клапан закрився;

- повідомлення про те, що другий клапан відкрився;

- повідомлення про те, що третій клапан закрився;

- повідомлення про те, що третій клапан відкрився.

Для кожного клапана число повідомлень про його закриття або відкриття буде однаковим і, як наслідок, ймовірності цих повідомлень рівні між собою, тобто

;

Використовуючи статистику спостережень, безпосередньо отримали інформацію про повідомлення і їх імовірності, що приведені в таблиці

Таблиця 5.1 Повідомлення і їх ймовірності

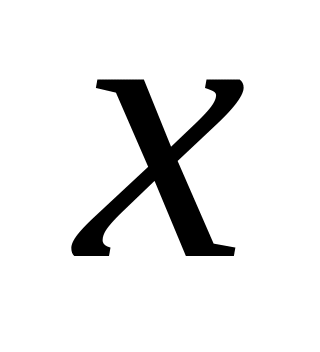
Р(х)	0,35	0,35	0,1	0,1	0,05	0,05

Тоді згідно формули:

[дв. од./повідом.],

маємо

або

[дв. од./повідом.]

Задача 2.

В об’єкті, аналогічному до описаного в задачі 1, проводиться періодичний контроль положення клапанів. Кількість повідомлень, що передаються про стан кожного клапана, однакова. Спостереженнями встановлено, що в середньому перший клапан закритий 98% часу, другий – 80%, третій – 60%. В решту часу ці клапани відкриті.

Визначити кількість інформації, яка міститься в одному повідомленні.

Розв’язок.

Позначимо через подію, яка полягає в тому, що передається повідомлення про стан клапана 1, - клапана 2, - клапана 3.

У зв’язку з тим, що всі клапани контролюються з однаковою частотою опитування, то ймовірності цих повідомлень рівні, тобто:

.

Положення клапанів «закрито» і «відкрито» несумісні, тому можна записати:

;

;

.

Із статистичних спостережень можна визначити для кожного клапана ймовірності їх закриття і відкриття:

Аналогічно для , , , .

За результатами розрахунку складаємо таблицю.

Таблиця 5.2 Повідомлення і їх ймовірності

х
р(х)	0,326	0,07	0,269	0,065	0,002	0,331
	0,527	0,05	0,509	0,256	0,017	0,528

В результаті отримаємо:

[дв. од./повідом.]