4.2 Основні положення теорії ймовірності

Основним поняттям, яким оперує теорія ймовірності, є випадкова величина, яка може приймати одне з різних значень, причому завчасно невідомо яке. Випадкові величини можуть приймати неперервний ряд значень (неперервні величини) і кінцевий ряд значень (дискретні величини).

Будь-яке з значень випадкової величини можна розглядати як випадкову подію, яка при дотриманні певних умов у процесі випробувань може як статися, так і не статися.

Припустимо, що в найпростішому випадку випадкова величина X приймати два значення: А і В. Проведемо кілька дослідів по визначенні числа реалізацій події А. Позначимо через N - загальну, кількість проведених дослідів і через n_А- число реалізацій події А.

Відношення числа реалізацій події А до загальної кількості дослідів називається частотою події А.

Повторюючи експеримент велику кількість разів і підраховуючи кожен раз частоту події , можна побудувати графік, приблизний вигляд якого показаний на рис. 4.2. Цей графік наглядно показує, що середні результати, отримані на підставі великої кількості дослідів з випадковими величинами, є статично стійкими, постійними.

Статична стійкість тут проявляється в тому, що із збільшенням числа випробувань N частота події буде дещо змінюватися і прямує до деякого визначеного значення, що називається ймовірністю події. Ймовірність події позначається Р(А), де в дужках вказується умовне позначення події.

Для нашого прикладу ймовірність події А знайдеться як границя відношення,

. (4.2)

Випадкові події А і В називаються несумісними, якщо вони не можуть статися одночасно. Так, при киданні монети не можуть одночасно випасти герб і надпис.

Ймовірність появи подій А або В, дорівнює сумі ймовірностей кожної з подій

(4.3)

Сума ймовірностей все можливих несумісних подій, що утворюють випадкову величину, дорівнює одиниці:

(4.4)

Розглянемо тепер імпульсну випадкову величину X, яка найпередбачуванішим чином може приймати дискретні значення х₁, х₂, …, х_k

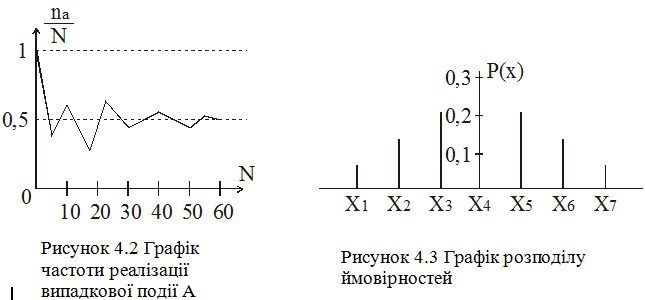
Припустимо, що в процесі спостереження за величиною X було зафіксовано всього N імпульсів, з яких n₁ імпульсів мали значення х₁, n₂ імпульсів – х₂ і т. д.

При необмеженому збільшенні числа спостережуваних імпульсів отримаємо відповідні ймовірності подій: для , для і т. д.

Значення ймовірностей характеризують випадкову величину X, яка може приймати значення .

Наглядним чином випадкова величина X може бути охарактеризована графіком розподілу ймовірностей, приблизний вигляд якого показано на рис. 4.3.

Для дискретної випадкової величини графік розподілу ймовірностей також носить дискретний характер. Критерієм нормування такого графіку є рівність

(4.5)

Сума ймовірностей можливих результатів випробувань випадкової величини X дорівнює одиниці.

Перейдемо далі до розгляду випадкової величини X, котра може прийняти будь-яке з неперервного ряду значень.

Ймовірність того, що дана величина X прийме якесь певне значення (наприклад х₁), очевидно, дорівнює нулю. Тому для характеристики неперервних випадкових величин доводиться користуватися поняттям ймовірності тої події, що значення досліджуваної величини опиниться в межах відрізку . Нехай в загальному випадку ймовірність такої події дорівнює . Візьмемо відношення

.

Границя цього відношення при називається густиною ймовірності

. (4.6)

Крива, що відображає залежність густини ймовірності р(х) від параметру х, називається диференційною функцією розподілу ймовірності. Приблизний вигляд такої функції показаний на рис 4.4, а. Він носить неперервний характер.

Рисунок 4.4 - Графіки функцій розподілу ймовірностей для неперервної випадковості величини х: а) – графік диференціальної функції; б) – графік інтегральної функції

Ймовірність тієї події, що значення випадкової величини Х виявиться в межах від х₁ до х₂, виражається через густину ймовірності знаходиться з рівняння

.

Диференційна функція розподілення ймовірності охоплює всі можливі значення параметру х. Тому ймовірність того, що значення величини Х виявиться в межах -  +, дорівнює одиниці, тобто

. (4.7)

Випадкова величина Х може бути також охарактеризована інтегральною функцією розподілу , яка визначає ймовірність тієї події, що значення величини Х опиниться визначеного рівня х₀.

.

Інтегральна функція розподілу ймовірностей легко може бути визначена за відомою диференційною функцією розподілу, з якою вона пов’язана рівнянням

. (4.8)

Для випадкових величин з дискретним числом рівнів графік інтегральної функції розподілу ймовірностей має вигляд драбинчастої кривої, що виростає до значення .

Неперервна випадкова величина описується неперервною функцією , приблизний графік якої даний на рис. 4.4, б. Критерієм нормування такого графіку є:

(4.9)

Другим поняттям, яким оперує теорія ймовірності, є випадковий процес. Під випадковим процесом розуміються зміни в часі фізичної системи, завчасно точно передбачити неможливо. Кількісно випадковий процес характеризується випадковою функцією часу, що складається з сімейства багатьох реалізацій.

Рисунок 4.5 - Випадкова функція часу

Розглянемо, для прикладу, характер зміни швидкості обертання двигуна конвеєра при пуску. Пуск двигуна є випадковим процесом. Характер зміни його швидкості залежить від кількості матеріалу на несучому органі конвеєра, величини напруги мережі, часу попередньої стоянки, якості змазки і т. д.

Якщо ми запишемо криву зміни швидкості обертання двигуна, то отримаємо першу реалізацію випадкової функції (рис. 4.5). Повторення цього досліду на іншій аналогічній установці дає другу реалізацію випадкової функції. Так, повторюючи з іншими двигунами конвеєрів, можна отримати випадкову функцію, що представляє собою сукупність окремих реалізацій. Якщо тепер сукупність реалізацій (рис. 4.5) розсікти часовою лінією, то отримаємо випадкову величину для моменту часу t₁. Ця величина утворюється сумою окремих випадком подій (на рис. 4.5 таких подій сім).

Для випадкової величини звичайним способом можуть бути визначені ймовірності усіх її значень (значень швидкості), що мають місце в заданий момент часу t₁.

При досить великому числі реалізацій (N) можна знайти ймовірність того, що при випадкова функція знаходиться нижче рівня n₁, тобто

.

Неважко бачити, що вказана ймовірність залежить як від фіксованого моменту часу, так і від вибраного рівня, тобто є функцією двох змінних t₁ і n₁. Ця функція

(4.10)

називається одновимірною інтегральною функцією розподілу ймовірностей випадкового процесу.

Окрім закону розподілу ймовірностей випадкової величини в фіксований момент часу для повної характеристики випадкового процесу необхідно знати вплив однієї випадкової величини на інші. Ця залежність випадкових величин, що називається кореляцією, буде розглянута пізніше.

Випадкові процеси можуть бути як стаціонарними, так і нестаціонарними.

Якщо для деякого випадкового процесу заміна t₁ - в рівнянні (4.10) на не змінює значення F₁, то такий випадковий процес називається стаціонарним. Зміщення по осі часу  може бути вибране довільно. Таким чином, ймовірні характеристики стаціонарного процесу не залежать від часу.

Більшість стаціонарних процесів володіє властивістю, яка називається ергодичністю. Ця властивість полягає в тому, що окрема реалізація випадкової функції, що зафіксована протягом досить тривалого часу, повністю визначає множину окремих реалізацій. Це означає, що встановлення статистичних характеристик випадкового процесу може бути проведено не на основі вивчення сукупності багатьох реалізацій, а на основі одної кривої, що спостерігається протягом тривалого часу Т.

Для багатьох досить вивчених випадкових процесів і явищ закони розподілу ймовірностей відомі, знайдені їх аналітичні вирази. Наприклад, випадкові величини з двома ймовірними значеннями досить повно описується біномінальним законом розподілу. Процеси, які носять масовий характер, підкоряються закону Пуасона чи Гауса.

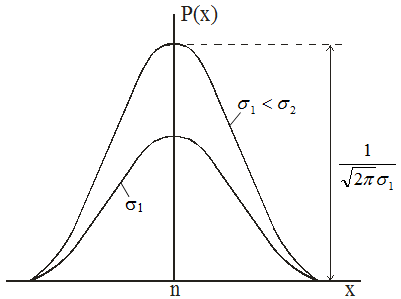
Рисунок 4.6 - Графік нормального розподілу густини ймовірностей

У телемеханіці для опису завад широко користуються законом Гауса або нормальним законом розподілу ймовірностей, при якому

. (4.11)

Тут  - середньоквадратичне відхилення;

а - середнє значення випадкової величини (математичне очікування).

Графік закону нормального розподілу густини ймовірностей показаний на рис. 4.6 для а=0 і різних значеннях . При а0 графік функції р(х) має ту ж форму але зсувається на величину а від початку осі х.

З рівняння (4.11) видно, що функція р(х) залежить тільки від двох постійних величин а і . Отже, для побудови кривої нормального розподілу необхідно знати тільки ці дві величини. Останні можуть бути знайдені за результатами випробувань.