3.4 Теорема Котельникова

Теорема Котельникова стверджує: якщо функція не вміщує частот більше ніж Fм, Гц, то вона повністю визначається своїми миттєвими значеннями в моменти часу, що відрізняються між собою на сек.

Розглянемо повідомлення, що передається протягом часу Т, яке описується неперервною функцією , що представлена на рис. 3.5.

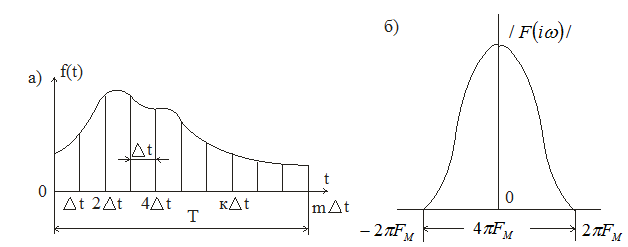
Рисунок 3.5 - Графік функції неперервного повідомлення та її частотний спектр: а) – графік функції ; б) – частотний спектр функції

Допустимо, що спектр цієї функції обмежений частотою F_м. Тоді якщо відліки проводити через інтервали часу

(3.7)

то функція може бути повністю відновлена за

(3.8)

значеннями.

Якщо відраховувати значення функції через інтервал більший, ніж , то повністю відновити неперервну функцію не вдасться. З іншого боку, якщо , то деякі значення імпульсів в послідовності, що описує неперервну функцію, є надлишковими в тому розумінні, що повне відновлення функції можливо і без їх участі.

На цій теоремі Котельникова базується вся сучасна теорія передачі неперервних повідомлень. Вона дозволяє будь – яке неперервне повідомлення з обмеженим спектром представити послідовністю коротких імпульсів, висота яких відповідає неперервній функції в дискретні моменти часу.

Нижче приводиться доведення теореми Котельникова.

Нехай комплексний спектр функції буде

, (3.9)

причому згідно умови при . Для наглядності комплексний спектр функції представлений у вигляді графіка на рис. 3.5. З цього графіка видно, що функція не вміщує складових з частотами, що перебільшують F_м.

Криву , як функцію часу, можна розкласти в ряд Фур’є з коефіцієнтами

, (3.10)

де n – порядок коефіцієнта ряду Фур’є.

За відомим частотним спектром можна знайти і функцію

. (3.11)

Прийнявши в це рівняння , знайдемо

. (3.12)

Порівняємо рівняння (3.10) і (3.12). Вони відрізняються знаком показника степеня і знаменником . Отже коефіцієнти С_n ряду Фур’є можуть бути знайдені з виразу

. (3.13)

Тут - значення функції в точках відліку, тобто в дискретні моменти часу:

або

Звідси можна зробити наступний висновок:

Якщо функція відома в точках відліку, то за рівнянням (3.14) можуть бути знайдені значення коефіцієнтів С_n ряду Фур’є, що визначають графік частотного спектру . В свою чергу частотний спектр , згідно рівняння (3.12), дозволяє знайти значення функції для будь – якого моменту часу, тобто повністю відновити функцію

Таким чином теорема Котельникова доведена.

Котельников показав також і спосіб відновлення функції за її миттєвими значеннями в дискретні моменти часу.

Ним отримано рівняння наступного виду:

. (3.14)

Тут - миттєві значення функції, відраховані через .

Рівняння (3.14) показує, що функція дорівнює сумі добутків визначаючих ординат на елементарну функцію виду

Графік елементарної функції показаний на рис. 3.6. Видно, що функція симетрична відносно точки відліку і має в ній максимальне значення, що дорівнює 1. У всіх інших точках відліку ця функція дорівнює нулю.

Рисунок 3.6 - Графік функції

Таким чином, для відновлення функції за її миттєвими значеннями в дискретні моменти часу необхідно, згідно рівняння (3.14), створити серію елементарних функцій , що пропорційні до визначаючих ординат функції в моменти відліку, і додати їх.

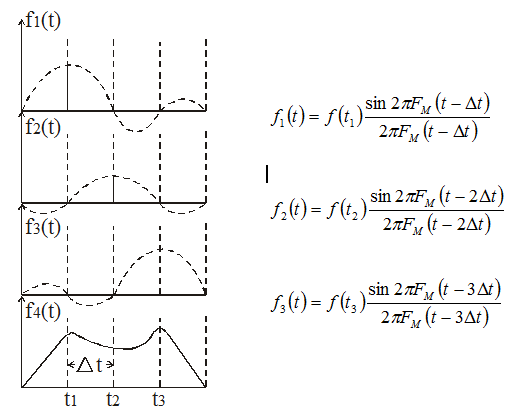
Рисунок 3.7 - Відновлення функції з обмеженим спектром по трьох складових

Для прикладу на рис. 3.7 дано відновлення неперервної функції за сумою трьох складових. Кожна з цих складових в момент відліку дорівнює , тобто миттєвому значенню функції або її визначаючою ординатою. У всіх інших точках відліку ця складова дорівнює нулю.

У реальних умовах передачі неперервних повідомлень загальне число визначаючих ординат, необхідне для повного відновлення повідомлення дуже велике.

Якщо час передачі повідомлення складає Т, то число визначаючих ординат буде . Так для передачі радіомовної програми при смузі пропускання протягом години буде необхідно

визначаючих ординат.

Терема Котельникова дозволяє також вибрати правильне співвідношення між тривалістю імпульсу , кількістю сигналів, що підлягають передачі, та іншими параметрами багатоканальної системи при часовому розділенні сигналів.