Тема 8 .Статистичне вивчення варіації.

Варіацією ознаки називають різницю у числових значеннях ознак одиниць сукупності та їх коливання навколо середньої величини, що характеризують сукупність.

До показників варіації відносяться: розмах варіації, середнє лінійне відхилення, дисперсія і середнє квадратичне відхилення.

Розмах варіації - різниця між максимальним і мінімальним значеннями ознаки :

R = X_max - X_min.

Середнє лінійне відхилення ( )являє собою середню арифметичну з абсолютних значень усіх відхилень індивідуальних значень ознаки від їх середньої.

= , де n - число членів ряду.

У чисельнику узяті різниці по модулю, оскільки алгебраїчна сума відхилень варіантів від їх середньої арифметичної завжди дорівнюватиме нулю.

Дисперсія ознаки - це середній квадрат відхилень варіантів від їх середньої величини.

Проста дисперсія:

=

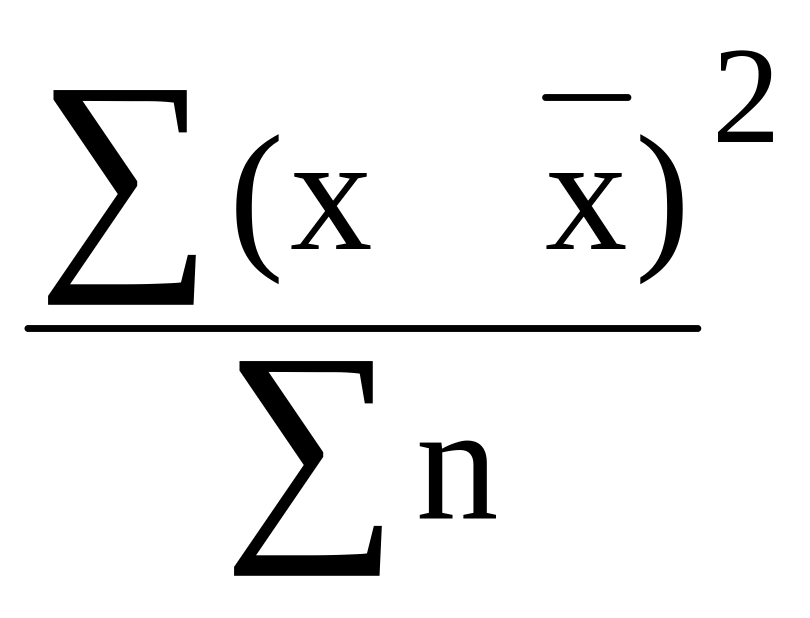
Зважена дисперсія для варіаційного ряду:

=

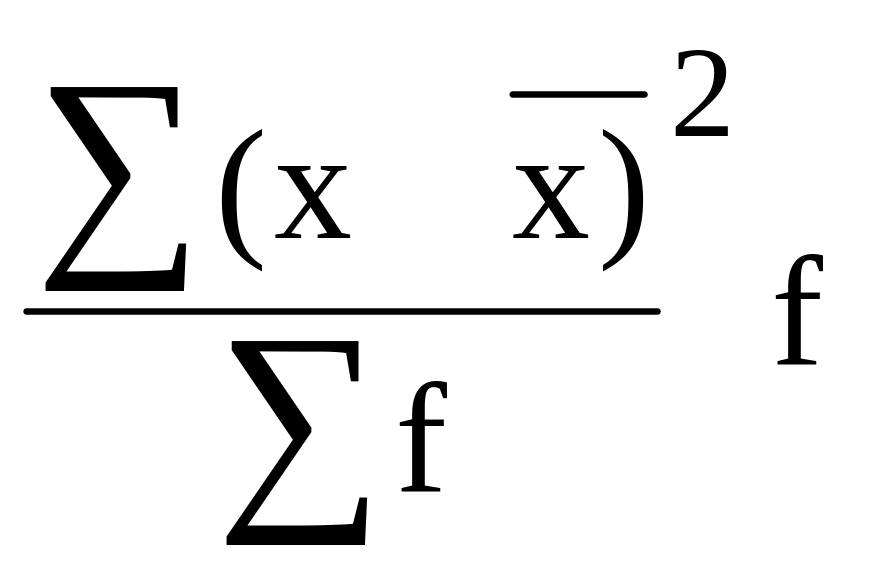
Середнє квадратичне відхилення () - дорівнює кореню квадратному з дисперсії. Це узагальнююча характеристика розмірів варіації ознаки.

В статистичній практиці часто виникає необхідність порівняння варіацій різних ознак. Для здійснення такого роду порівнянь використовують відносні показники варіації.

Ці показники обчислюються як відношення абсолютних показників варіації до середньої арифметичної або медіани. Використовуючи в якості абсолютних показників розмах варіації, середнє лінійне, середнє квадратичне та квартильне відхилення, отримаємо відносні показники варіації:

Коефіцієнт осциляції :

Відносне лінійне відхилення:

Коефіцієнт варіації:

Відносний показник квартильной варіації :

Сукупність вважається однорідною, якщо коефіцієнт варіації не перевищує 33 %.

Тема 9. Види і взаємозв’язок дисперсій.

Міжгрупова дисперсія. Середня з групових дисперсій. Правило розкладання (декомпозиції) дисперсій. Кореляційне відношення.

Варіація ознаки обумовлена різними чинниками, деякі з цих чинників можна виділити, якщо статистичну сукупність розбити на групи за якою-небудь ознакою. Тоді разом з вивченням варіації ознаки і усієї сукупності в цілому стає можливим вивчити варіацію для кожної із складових її групи, а також між цими групами.

У простому випадку, коли сукупність розбита на групи по одному чиннику, вивчення варіації досягається за допомогою числення і аналізу трьох видів дисперсії: загальною, міжгруповою, внутрішньогруповою.

Загальна дисперсія вимірює варіацію ознаки по усій сукупності під впливом усіх чинників, що обумовлюють цю варіацію. Вона дорівнює середньому квадрату відхилень окремого

Значення ознаки від загальної середньої і може бути вичислена як проста і зважена дисперсія.

Проста загальна дисперсія:

Зважена загальна дисперсія:

Міжгрупова дисперсія (²) характеризує систематичну варіацію результативної ознаки, обумовлену впливом ознаки чинника, покладеного в основу групування. Вона дорівнює середньому квадрату відхилень групових середніх від загальної середньої.

Внутрішньогрупова дисперсія відбиває випадкову варіацію, обумовлену впливом неврахованих чинників і незалежну від ознаки чинника, покладеного в основу групування. Вона дорівнює середньому квадрату відхилень окремих значень ознаки в середині групи від середньої арифметичної цієї групи і може бути обчислена як проста, так і зважена дисперсія.

Проста внутрішньогрупова дисперсія

Зважена внутрішньогрупова дисперсія

На підставі внутрішньогрупової дисперсії по кожній групі можна визначити загальну середню з внутрішньогрупових дисперсії.

Загальна середня з внутрішньогрупових дисперсій:

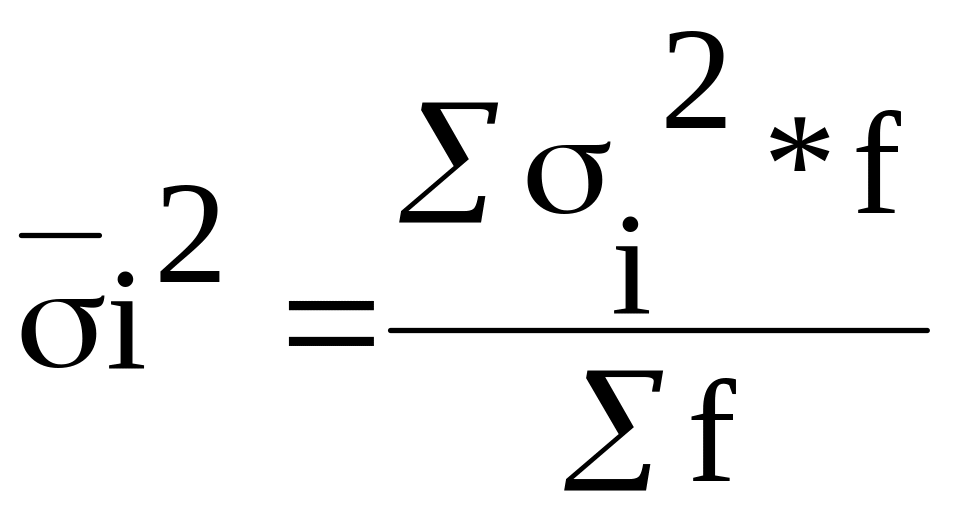
Згідно з правилом розкладання (декомпозиції) дисперсій, загальна дисперсія дорівнює сумі середньою з внутрішньогрупових і міжгруповій дисперсії.

Загальна дисперсія:

У статистичному аналізі широко використовується емпіричний коефіцієнт детермінації ² - показник, що є долею міжгрупової дисперсії в загальній дисперсії результативної ознаки і характеризує силу впливу групувальної ознаки на утворення загальної варіації.

Коефіцієнт детермінації :

За відсутності зв'язку емпіричний коефіцієнт детермінації дорівнює 0, а при функціональному зв'язку - рівний 1.

Емпіричне кореляційне відношення - показує тісноту зв'язку між груповою і результативною ознакою. Набуває значень від 0 до 1 і дорівнює кореню квадратному з емпіричного коефіцієнта детермінації :

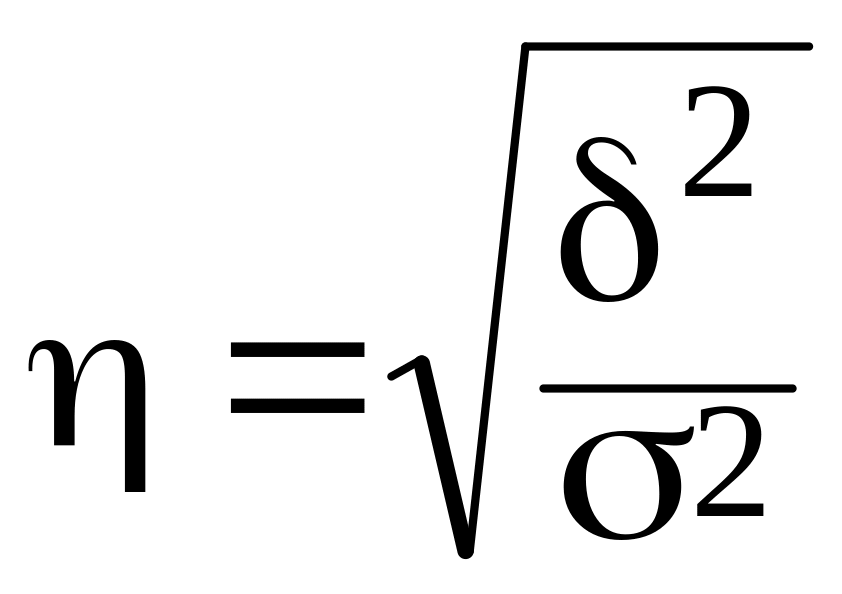
Якщо зв'язок відсутній, то кореляційне відношення дорівнює 0, а якщо зв'язок функціональний то 1.