2. Запись полей в волноводе для любого типа волн

Поперечные составляющие полей и (они всегда ортогональны) для волны любого типа могут быть записаны в следующей форме

(1.1)

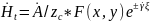
где 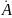– является комплексной амплитудой поля соответствующей волны; F(x,y) – описывает закон распределение поля в поперечной плоскости линии передачи;

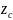- характеристическое сопротивление линии (рассмотрено ниже);

- коэффициент распространения; - постоянная затухания, 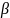- коэффициент фазы.

Знак минус в экспоненте ставится, если при распространении волны координата  возрастает, знак плюс - если уменьшается, зависимость поля от времени имеет вид .

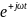Составляющие и 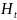ортогональны между собой.

3. Дополнительные определения

Режим распространения волны вдоль линии носит название - режим бегущей волны, если в ЛП существует волна фиксированного типа, распространяющаяся только в одном направлении.

Падающая волна – бегущая волна, распространяющаяся от выбранного сечения вдоль линии в направлении от источника, характеризуется амплитудой при множителе

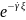
Отраженная волна– бегущая волна, возникшая за счет отражения падающей волны от нерегулярности в линии и распространяющаяся навстречу падающей. Характеризуется амплитудой при множителе .

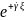Режим смешанных волн – возникает при одновременном присутствии в линии падающей и отраженной волн, при этом за счет их интерференции появляется периодическое изменение амплитуд полей Е и Н вдоль линии.

В случае, когда амплитуды падающей и отраженной волн равны, режим называется режимом стоячих волн.

1.2.4. Длина волны в линии передачи

Длина волны в линии передачи ( ) – это расстояние вдоль линии передачи, на котором фаза бегущей волны заданного типа меняется на 2.

Фаза 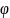в бегущей волне в зависимости от координаты определяется из соотношения 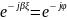, = 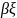и меняется по линейному закону в зависимости от координаты .

Поскольку на расстоянии, равном длине волны в тракте - _в, фаза меняется на 2, из соотношения _в=2 следует, что =2/_в.

Для волны типа Т длина волны в линии находится как

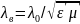; (1.2)

для волн типа Е и Н

. (1.2’)

здесь - величины относительных магнитной и диэлектрической проницаемостей среды, заполняющей пространство, окружающее проводники. Для воздуха обе величины равны 1.

1.2.5. Фазовая скорость V_ф

Скорость перемещения фазового фронта вдоль линии обозначим как 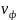. Если временная зависимость выбрана в виде , то 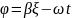. Приравняем нулю - 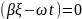и рассмотрим движение фронта волны с нулевой фазой вдоль линии. Тогда фазовую скорость можно определить из следующих соотношений:

откуда

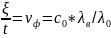
Для волны типа Т

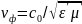(1.3)

Для волн типа Е и Н имеет место дисперсия, в результате которой при приближении ₀ к _кр фазовая скорость стремится к бесконечности.

(1.3’)

1.2.6. Понятие характеристического сопротивления

Характеристическое сопротивление определяется как отношение амплитуд поперечных составляющих полей Е_t и Н_t в бегущей волне заданного типа

Для волны типа Т

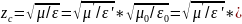120π ом (1.4)

где ₀₌ 4π×10^-7гн/м; ₀ = 10^-9/36π ф/м;

Для волн типа Н и Е величина определяется из соотношений:

- в случае волны типа Н

(1.4’)

- в случае волны типа Е

Пр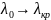и характеристическое сопротивление волны типа Е стремится к нулю, а волны типа - Н к бесконечности.