
- •Вопрос 12
- •Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.
- •Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.
- •Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- •Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
- •Вопрос 13
- •Вопрос 14
- •Вопрос 15 Дифференцируемость функции в точке, дифференциал
- •Вопрос 16
- •Вопрос 17
- •Производная функции, заданной неявно
- •Вопрос 18
- •Вопрос 19
- •3. Градиент
- •4. Касательная плоскость а нормаль к поверхности
- •Вопрос 20
- •Вопрос 21
- •Обозначение двойного интеграла
- •Геометрический смысл двойного интеграла.
- •1. Случай прямоугольника.
- •§ 2. Основные свойства двойного интеграла
- •Вопрос 22
- •Вопрос 23 § 3. Геометрические и физические приложения определенного интеграла
- •1. Вычисление площади в декартовых координатах
Вопрос 12
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
Область интегрирования является бесконечной. Например, является бесконечным интервалом
 .
.Функция f(x) неограничена в области интегрирования.
Если интервал [a,b] конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла.
Несобственные интегралы I рода[править | править исходный текст]
Пусть ![]() определена
и непрерывна на множестве от
и
определена
и непрерывна на множестве от
и 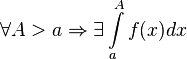 .
Тогда:
.
Тогда:
Если
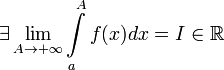 ,
то используется обозначение
,
то используется обозначение 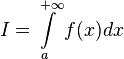 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
называется
сходящимся.Если не существует конечного
 (
(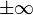 или
или 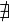 ),
то интеграл
),
то интеграл 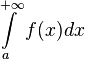 называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть
определена
и непрерывна на множестве от ![]() и
и 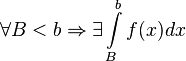 .
Тогда:
.
Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.
Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.
Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
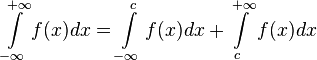 ,
где с — произвольное число.
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I рода[править | править исходный текст]
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры[править | править исходный текст]

Несобственные интегралы II рода[править | править исходный текст]
Пусть
определена
на ![]() ,
терпит бесконечный разрыв в точке x=a
и
,
терпит бесконечный разрыв в точке x=a
и 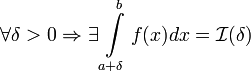 .
Тогда:
.
Тогда:
Если
 ,
то используется обозначение
,
то используется обозначение 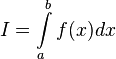 и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.Если
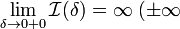 или
или  ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а 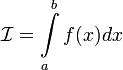 называется
расходящимся к
,
или просто расходящимся.
называется
расходящимся к
,
или просто расходящимся.
Пусть
определена
на ![]() ,
терпит бесконечный разрыв при x=b и
,
терпит бесконечный разрыв при x=b и 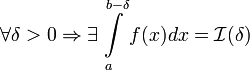 .
Тогда:
.
Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Если
функция
терпит
разрыв во внутренней точке ![]() отрезка
отрезка ![]() ,
то несобственный интеграл второго рода
определяется формулой:
,
то несобственный интеграл второго рода
определяется формулой:
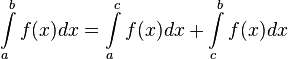
Геометрический смысл несобственных интегралов II рода[править | править исходный текст]
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции
Пример[править | править исходный текст]

Отдельный случай[править | править исходный текст]
Пусть
функция
определена
на всей числовой оси и имеет разрыв в
точках ![]() .
.
Тогда
можно найти несобственный интеграл 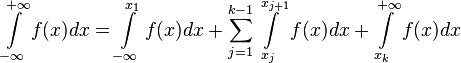
Критерий Коши[править | править исходный текст]
1.
Пусть
определена
на множестве от
и 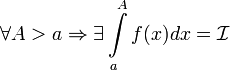 .
.
Тогда 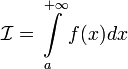 сходится
сходится 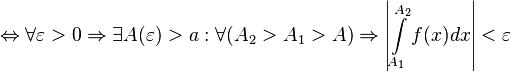
2.
Пусть
определена
на
и 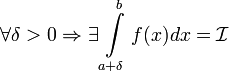 .
.
Тогда
сходится 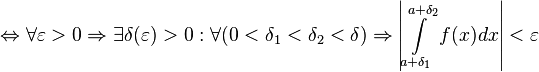
Абсолютная сходимость[править | править исходный текст]
Интеграл 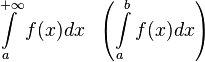 называется абсолютно
сходящимся,
если
называется абсолютно
сходящимся,
если  сходится.
Если
интеграл сходится абсолютно, то он
сходится.
сходится.
Если
интеграл сходится абсолютно, то он
сходится.
Условная сходимость[править | править исходный текст]
Интеграл  называется условно
сходящимся,
если
сходится,
а
называется условно
сходящимся,
если
сходится,
а  расходится.
расходится.
