
- •Классическая электронная теория металлов (кэт) Природа носителей тока в металлах
- •Опыт Рикке
- •Опыты Стюарта и Толмена (идея Мандельштама и Папалекси)
- •Электромагнетизм Магнитное поле и его характеристики Обнаружение магнитного поля
- •Направление линий магнитной индукции
- •Наблюдение магнитных полей
- •Магнитное поле Земли
- •Поле макро- и микротоков Гипотеза Ампера
- •Принцип суперпозиции. Закон Био – Савара – Лапласа Принцип суперпозиции
- •Закон Био-Савара-Лапласа и его применение к расчету полей
- •Взаимодействие параллельных токов
- •Движение заряженных частиц в магнитном поле
- •Вдоль линии магнитной индукции
- •Перпендикулярно вектору
- •Эффект Холла
- •Механизм возникновения поперечного электрического поля
- •Холловская разность потенциалов
- •Постоянная Холла
- •Определить концентрацию носителей тока в проводнике (при известных характере проводимости и заряде носителей);
- •Судить о природе проводимости полупроводников, так как знак постоянной Холла совпадает со знаком заряда eтока. Теорема о циркуляции вектора магнитной индукции в вакууме
- •Поток вектора магнитной индукции Теорема Гаусса для вектора магнитной индукции
- •Работа по перемещению проводника с током в магнитном поле
- •Теорема о циркуляции вектора напряженности магнитного поля
- •Парамагнетики, диамагнетики, ферромагнетики
- •Электромагнитная индукция Явление электромагнитной индукции
- •Закон электромагнитной индукции (закон Фарадея)
- •Энергия магнитного поля
- •Ток смещения
- •Уравнения Максвелла
- •Электромагнитные колебания Колебательный контур
- •Уравнение колебательного контура
- •Свободные незатухающие колебания в контуре
- •Свободные затухающие колебания в контуре
- •Вынужденные колебания в контуре
- •Электрический резонанс. Резонансные кривые
- •Волны Волновое уравнение для электромагнитного поля
- •Свойства электромагнитных волн
- •Энергия и импульс электромагнитной волны
- •Шкала электромагнитных волн
Закон Био-Савара-Лапласа и его применение к расчету полей
Закон
Био-Савара-Лапласа – определяет в точке
А индукцию поля
![]() создаваемую
элементом проводника
создаваемую
элементом проводника
![]() c
током J
на расстоянии rот
него.
c
током J
на расстоянии rот
него.


-
вектор, по модулю равный длине
![]() элемента
проводника и совпадающий по направлению
с током;
элемента
проводника и совпадающий по направлению
с током;
![]() -
радиус – вектор, проведенный из элемента
проводника
в точку А поля; r
– модуль радиуса-вектора
;
=
4π∙10-7
Н/м2
=
4π∙10-7
Гн/м – магнитная постоянная;
-
безразмерная величина – магнитная
проницаемость среды.
-
радиус – вектор, проведенный из элемента
проводника
в точку А поля; r
– модуль радиуса-вектора
;
=
4π∙10-7
Н/м2
=
4π∙10-7
Гн/м – магнитная постоянная;
-
безразмерная величина – магнитная
проницаемость среды.

Направление вектора
Вектор перпендикулярен и , направлен по касательной к линии магнитной индукции. Направление определяется по правилу правого винта: направление вращения головки винта дает направление , если поступательное движение винта соответствует направлению тока в элементе.
Магнитное поле прямого тока
Ток течет по тонкому прямому проводнику бесконечной длины. На расстоянии R находится точка А, в которой надо показать направление и рассчитать магнитную индукцию.

За
постоянную интегрирования выбираем
угол
,
который для всех элементов прямого
провода изменяется от 0 до
![]() .
.
Получаем

Магнитное поле в центре кругового проводника с током

 (учли,
что r=R,
sin
=
1)
(учли,
что r=R,
sin
=
1)

Закон Ампера. Взаимодействие параллельных токов
Закон
Ампера

Модуль
силы Ампера
![]()
Закон
Ампера определяет силу![]() ,
с
которой магнитное поле с индукцией
действует
на элемент проводника с токомJ,
-
угол между
и
.
,
с
которой магнитное поле с индукцией
действует
на элемент проводника с токомJ,
-
угол между
и
.
Направление силы Ампера определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера (см. рис).
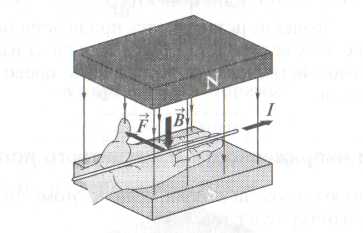
Взаимодействие параллельных токов
Два
параллельных проводника с токами![]() и
и![]() находятся
на расстоянии R
друг
от друга (см. рис).
находятся
на расстоянии R
друг
от друга (см. рис).

Направление
силы![]() ,
с
которой магнитное поле
,
с
которой магнитное поле
![]() (создается
проводником с током
)
действует на участок
второго
тока, определяется по правилу левой
руки (также определяется и направление
силы
(создается
проводником с током
)
действует на участок
второго
тока, определяется по правилу левой
руки (также определяется и направление
силы
![]() ).
).

Проводники с токами одинакового направления притягиваются, с токами разного направления – отталкиваются.

Сила взаимодействия на единицу длины проводника

Два параллельных проводника с током находятся в вакууме ( = 1).
Единицы магнитной индукции В и напряженности Н магнитного поля
Единица магнитной индукции: 1 Тл = 1 Н/ (А ∙ м) (Тл – тесла)
Единица напряженности магнитного поля: 1 А/м – напряженность такого поля, магнитная индукция которого в вакууме равна: 4π ∙10-7 Тл.
![]()

Движущиеся заряды и магнитные поля
Магнитное поле движущегося заряда
Магнитная индукция

Модуль магнитной индукции

-
радиус-вектор, проведенный из заряда
Qк
точке наблюдения М;
-
угол между
![]() .
Записанный
закон определяет магнитную индукцию
положительного заряда, движущегося со
скоростью
.
Записанный
закон определяет магнитную индукцию
положительного заряда, движущегося со
скоростью![]() .
Если движется отрицательный заряд, то
Q
надо
заменить на –Q.
.
Если движется отрицательный заряд, то
Q
надо
заменить на –Q.
Вектор направлен перпендикулярно плоскости, в которой расположены векторы .

Сила Лоренца

Модуль силы Лоренца
![]()
Сила Лоренца – сила, с которой магнитное поле действует на движущиеся заряды.
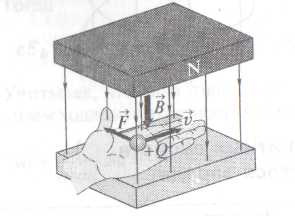
Направление
силы Лоренца определяется с помощью
правила
левой руки: если ладонь левой руки
расположить так, чтобы в нее входил
вектор
,
а
четыре вытянутых пальца направить вдоль
вектора
(для
![]() >0
направления
I
и
совпадают,
для
<0
– противоположны), то отогнутый большой
палец покажет направление силы,
действующий на положительный заряд.
>0
направления
I
и
совпадают,
для
<0
– противоположны), то отогнутый большой
палец покажет направление силы,
действующий на положительный заряд.
Сила Лоренца не совершает работы. Магнитное поле не действует на покоящийся электрический заряд. Магнитное поле действует только на движущиеся в нем заряды.
Формула
Лоренца
определяет силу, если на движущийся
заряд одновременно действуют магнитное
поле с индукцией
и
электрическое поле с напряженностью![]() .
.
![]()
