5 Аналітичний і числовий розв’язки математичної моделі обєкта

5.1 Аналітичний розв’язок математичної моделі об’єкта

Запишемо лінеаризовану математичну модель об’єкта в у векторно-матричному вигляді

. (5.1)

Для об’єкта з двома входами і двома виходами

, ,

, .

Перетворимо рівняння (5.1) за Лапласом при нульових початкових умовах

.

Із останнього рівняння знаходимо

. (5.2)

За визначенням матричної передавальної функції

. (5.3)

Порівнюючи (5.2) і (5.3), приходимо до висновку, що

. (5.4)

Матричну передавальну функцію об’єкта можна подати і в іншому виді

. (5.5)

Векторне рівняння (5.3) запишемо у розгорнутому вигляді

.

Виконавши у правій частині останнього рівняння операцію множення над матрицям, отримаємо

, (5.6)

. (5.7)

Для заданих зображень вхідних дій і можна знайти і , використавши теорему про лишки.

Допустимо, що можна записати у вигляді відношення двох поліномів:

, (5.8)

a – полюси функції , які знаходяться шляхом розв’язку алгебраїчного рівняння . Тоді

, (5.9)

де – для простих полюсів , і

для кратних полюсів з кратністю .

5.2 Числовий розв’язок математичної моделі об’єкта

Для розв’язку моделі числовим методом скористаємося матрично-векторною формою (5.1) подачі системи диференціальних рівнянь. Тоді можна скористатись методом Рунге-Кутта розв’язку систем диференціальних рівнянь, маючи на увазі, що

.

6 Приклад дослідження властивостей об'єкта за допомогою математичних моделей

Як приклад розглянемо об’єкт, функціональна схема якого показана на рис. 6.1. Поставимо задачу – створити і дослідити математичну модель гідравлічного об’єкта.

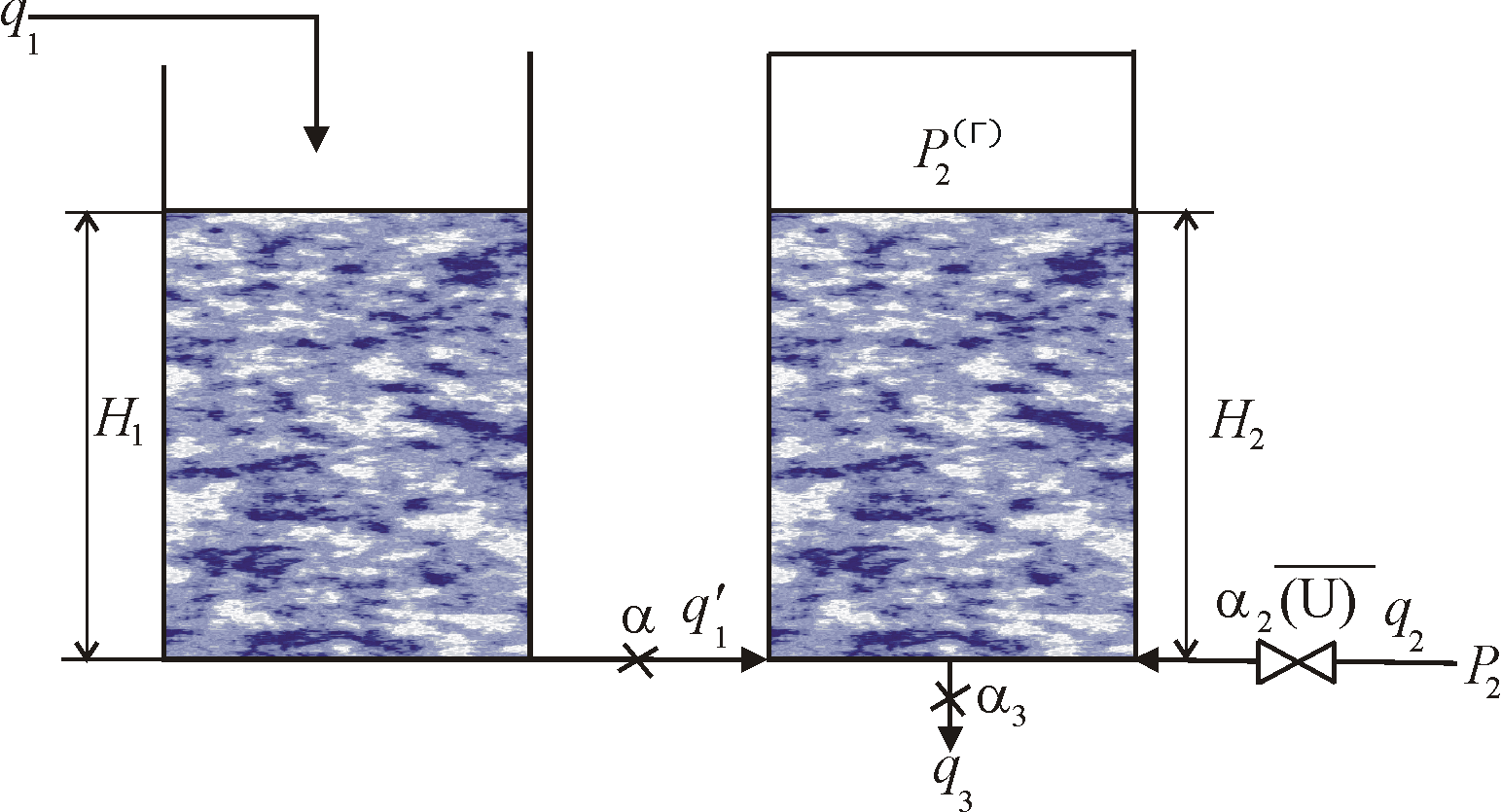
Рисунок 6. 1 – Функціональна схема гідравлічного об’єкта.

6.1 Математична модель об’єкта

Математичну модель об’єкта будемо складати при таких допущеннях:

• густина рідини постійна і не залежить від температури;

• поперечні січення вздовж довжини резервуара постійні і мають форму круга;

• тиск , під яким рідина поступає в резервуар постійний;

• газ над рідиною в ємностях є ідеальним.

В основу математичної моделі покладемо рівняння матеріального балансу.

Для першої ємності:

. (6.1)

Для другої ємності:

, (6.2)

де М₁ і М₂ – маси рідини у першій та другій ємностях відповідно;

- масові витрати рідини.

Масова витрата рідини обчислюється за формулою:

,

де - тиск над рідиною в першій ємності.

Обчислимо тепер значення витрати, яка витікає з другої ємності.

.

де ₃ – гідравлічний опір витіканню рідини з ємності. Приймаємо ₃ =const.

Знаходимо значення витрати на вході другої ємності.

.

де ₂(U) - гідравлічний опір витіканню рідини з ємності, що залежить від керуючої дії U.

Маса рідини в ємностях – це добуток густини рідини  на її об’єм V.

, i=1,2,

де , i=1,2.

Підставляючи значення в формули (6.1) і (6.2), отримуємо

, (6.3) (6.4)

Для ідеального газу маємо , де R – газова постійна; - маса газу над рідиною в другій ємності;  - молярна маса газу; Т – температура газу.

Оскільки T=const, і =const, то . З іншої сторони . Так як , то .

Отже,

. (6.5)

Підставляючи значення (6.5) в формули (6.3) і (6.4) приходимо до висновку, що

( 6.6)

,

(6.7)

Рівняння (6.6) і (6.7) утворюють математичну модель технологічного об’єкта.