2 Методика побудови математичних моделей типових об’єктів

Сучасні методи синтезу замкнутих систем керування опираються, як правило, на апріорні відомості про динамічні характеристики керованих об’єктів (КО). Математичний опис КО служить вихідним матеріалом для аналізу і синтезу всієї замкнутої системи керування. Якщо такий опис невідомий, то теорія не може дати правильної відповіді на питання, які виникають в процесі проектування автоматичної системи керування (АКС).

Математичну модель КО можна визначити двома способами. Можна або ідентифікувати систему за результатами експерименту, або шукати необхідний математичний опис розрахунковим шляхом, використовуючи загальні фізичні закони, відомості про конструкцію і технологічні параметри обладнання.

Кожний із методів має свої переваги і недоліки. Експериментальний спосіб можна реалізувати лише тоді, коли система, що досліджують уже побудована. Якщо експеримент поставлений правильно, то можна одержати необхідну інформацію про поведінку системи, досліджуючи вже існуючі промислові об’єкти. Але при цьому, як правило, неможливо одержати повну уяву про внутрішню структуру системи, про всі взаємозв’язки і вказати, як динамічні характеристики можуть вплинути на вибір найкращої конструкції.

Фізико-математичний аналіз процесів, які протікають в системі, дає можливість одержати математичну модель навіть в тих випадках, коли система знаходиться ще на стадії проектування.

Незважаючи на те, що точні значення всіх параметрів, які необхідні для аналітичного розрахунку (наприклад, коефіцієнтів теплопередачі, коефіцієнтів гідравлічного опору і т.п.) часто невідомі, фізико-математичний аналіз дає можливість вибрати певну структуру математичної моделі КО, параметри якого можуть бути додатково уточнені експериментально.

Виходячи із специфіки задач керування будь-який технологічний процес може бути умовно зображений так як це показано на рис.2.1.

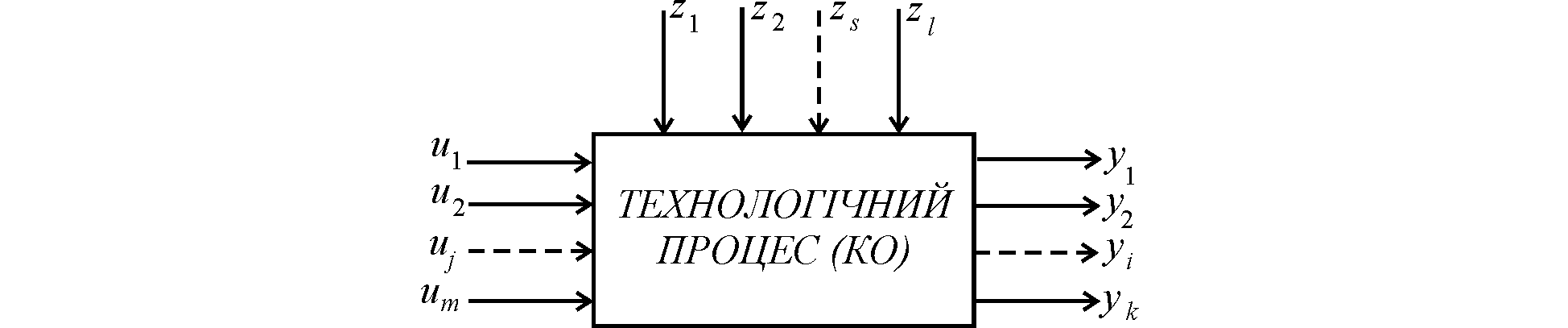
Рисунок 2.1 - Умовне зображення технологічного процесу

Всі вхідні і вихідні величини КО можна поділити на три групи.

Перша група: керуючі дії, , . Під керуючими діями розуміють ті вхідні величини, за допомогою яких можна змінити стан керованого об’єкта у відповідності з метою керування. Керуючими діями можуть бути матеріальні або енергетичні потоки.

Друга група: збурюючі дії , - це параметри, значення яких випадково змінюється з плином часу. Особливістю цих величин є те, що їх часто неможливо виміряти. Це можуть бути різні домішки у вихідній сировині, зміна параметрів навколишнього середовища, зміна властивостей матеріалів, обладнання, його геометричних розмірів і т.п. Перша і друга групи утворюють вхідні величини об’єкта.

Третя група: вихідні параметри у_i , визначаються режимом процесу і характеризують його стан, який виник в результаті спільних дій вхідних величин і z_j. З цієї причини вихідні величини ще називають змінними стану. Варто відзначити, що термін “змінні стану” являється більш широким, ніж термін “вихідні величини”. Оскільки, під вихідними величинами розуміють тільки характеристики продукції, тоді як параметри стану можуть бути довільні фізичні величини (навіть абстракції), наприклад, характеристики режиму процесу – температура, витрати, тиск, тощо.

Для зображення сукупності вхідних і вихідних величин часто будемо застосовувати векторну форму запису: ; .

Тоді в загальному випадку математична модель технологічного процесу буде подана системою диференціальних рівнянь:

(2.1)

з початковим умовам ..., або .

В залежності від ступеня випадкової дії вектора на вектор виходу моделі ділять на стохастичні і детерміновані. Якщо вплив на процес незначний і його можна не приймати до уваги, то модель називають детермінованою. В противному разі модель буде стохастичною. Зміна може входити в праві частини системи рівнянь (2.1) як в явному так і в неявному вигляді. В першому випадку модель називають нестаціонарною, а в другому – автономною.

При математичному описі об’єктів моделювання основною задачею є одержання системи диференціальних рівнянь (2.1). Для розв'язку цієї задачі найбільш часто застосовують поелементний опис об’єкта. Рівняння окремих елементів складають на основі тих фізичних законів, які характеризують роботу того чи іншого елемента. Такими законами можуть бути закони механіки, електротехніки, теплотехніки, гідравліки. Складаючи диференціальні рівняння окремих елементів системи, бажано якнайточніше відтворити поведінку того чи іншого елемента. Але складність одержаних рівнянь перешкоджає одержанню їх розв’язків та дослідженню властивостей елементів. Тому при складанні диференціальних рівнянь необхідно досягти розумного компромісу між бажаним повним описом поведінки елементу і можливістю одержання розв’язку та його дослідження.

При математичному моделюванні КО рекомендується певна послідовність дій, яку можна розділити на такі стадії.

Перша стадія – можливо найбільш важлива – це постановка задачі, яка визначає не тільки мету синтезу системи, але й шляхи розв'язання конкретної задачі.

Друга стадія – визначення фундаментальних законів, яким підкоряються механізми явищ, що лежать в основі проблеми. Теоретичні основи процесів визначаються, як правило, із різних опублікованих джерел.

Третя стадія – виявлення вхідних і вихідних величин КО і введення позначень для цих величин. З цієї групи величин слід виявити керуючі дії, зміною яких можна досягти мети керування. Потім на основі вибраної фізичної моделі стосовно до задачі, яка розв’язується записують систему рівнянь у формі (2.1). При цьому вивчають можливість спрощення рівнянь шляхом нехтування незначними членами. Відкидаючи їх, треба бути обережним і впевнитись в тому, що відкинутий член незначно впливає на розв’язок відповідного диференціального рівняння.

Четверта стадія – вибирається один із можливих розв’язків системи диференціальних рівнянь (2.1) з метою аналізу моделі.

П’ята стадія – аналіз моделі. Якщо необхідно розв’язати нескладне питання і рівняння досить прості, то відповідь одержують шляхом аналізу моделі, не розв’язуючи систему рівнянь(2.1). Більш складний рівень аналізу пов’язаний з розв’язком рівнянь (2.1) аналітичними (якщо це можливо) або числовими методами.