24. Комбинированный метод расчёта в сечениях ферм.

В ряде случаев для определения уси-лий бывает необходимо проводить одновременно два или несколько сече-ний, составлять и решать систему уравнений. Примером этого может служить полураскосная ферма, усилия в полураскосах которой определяютспособом двойных сечений.

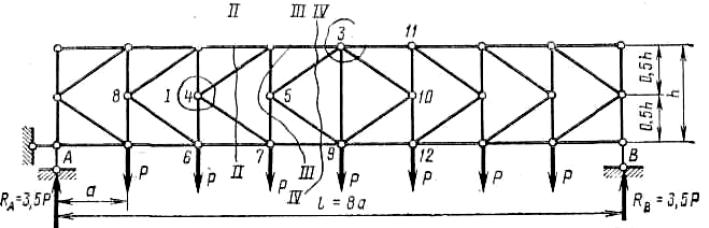
Пример 4.4. Определить усилия в стержнях фермы, показанной на рис. 4.4. Предварительно определим опорные реакции: RA = RB = 3,5P.

Вырежем узел 4 круговым сечением I и составим уравнение проекций сил на горизонтальную ось (рис. 4.4 и 4.5, а): ΣX = N42 sinα + N47 sinα = 0; N42 = −N47.

Далее разрежем ферму сечением II–II, отбросим правую часть, а для левой части составим уравнения проекций сил на вертикальную ось: ΣY лев = N42 cos α − N47 cos α + 3,5 P − P − P =0

N47 = 0,75P/cosα; N42 = −0,75P/cosα.

Вырежем узел 2 (см. рис. 4.4 и 4.5, б) и, составив уравнение проекций на вертикальную ось, найдем усилие в стержне 2 – 5, а затем, вырезав узел 7 (рис. 4.5, в), – усилие в стержне 5 – 7: ΣY = −N24 cosα − N25 = 0; N25 = 0,75P; ΣY = N47 cosα + N57 − P = 0; N57 = 0,25P

Р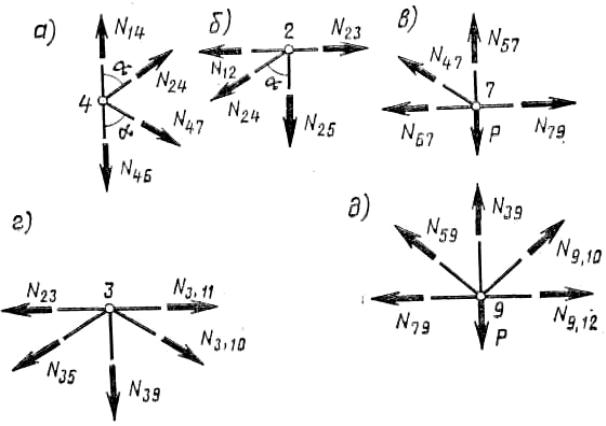 азрежем ферму сечением III–III и, составив уравнения моментов Σ = 0 и Σ = 0,

найдем усилия в стержнях 2 – 3 и 7 – 9:

Σ = 3,5P ⋅ 3a − P ⋅ 2a − Pa + N23 h = 0; N23 = − 7,5Pa/h;

Σ = 3,5P ⋅ 3a − P ⋅ 2a − Pa − N79 h = 0; N79 = 7,5Pa/h.

Отметим, что, зная N23, значение усилия N79 можно найти из уравнения проекций сил, действующих на левую часть фермы, на горизонтальную ось:

ΣX = N23 + N79 = 0; N79 = −N23.

Для определения усилия в стержне 3 – 9 предварительно вырежем круговым сечением узел 5, составим уравнение проекций на горизонтальную ось и получим N53 = −N59 . Далее рассечем ферму сечением IV–IV, отбросим правую часть, а для левой части составим уравнение проекций сил на вертикальную ось: ΣY лев = N 35 cos α − N59 cos α + 3,5 P − 3P =0

откуда найдем: N35 = −0,25P/ cosα, N59 = 0,25P/ cosα. Исходя из симметрии фермы и нагрузки усилия в симметрично расположенных стержнях 3 – 5 и 3 – 10, а также 5 – 9 и 9 – 10 равны:

N3,10 = N53 = −0,25P/ cosα, N9,10 = N59 = 0,25P/ cosα. И тогда, вырезав круговым сечением узел 3 и составив уравнение проекций на вертикальную ось (рис. 4.5, г): ΣY = −N35 cosα − N3,10 cosα − N39 = 0;

после подстановки значений N35 и N3,10 получим N39 = 0,5P . Если круговым сечением вырезать узел 9 и составить уравнение проекций на вертикальную ось (рис. 4.5, д) ΣY = N59 cosα − N9,10 cosα + N39 − P = 0, то также получим, как и следовало ожидать, N39 = 0,5Р.