15. Линии влияния изгибающего момента и поперечной силы в балке.

Линия влияния изгибающего момента в данном сечении.

Изгибающий момент в данном сечении балки равен сумме моментов внешних сил, приложенных к отсеченной части балки, относительно центров тяжести сечения. При движении груза справа от сечения (рис. 29, а) в сумму моментов левых сил войдет только левая реакция, а при движении груза слева от сечения в эту сумму моментов следует включить и момент от груза. Таким образом, имеем два отличных друг от друга аналитических выражения для изгибающего момента. Рассмотрим движение груза справа от сечения, когда х меняется от аk до l. Составляя сумму моментов левых сил при грузе справа от сечения,получаем:

Рассмотрим теперь движение груза Р = 1 слева от сечения, т. е. когда х меняется от 0 до ak. Определяем изгибающий момент Мk по правым силам получим: т. е. закон изменения изгибающего момента при движении груза слева от сечения получается как закон правой реакции В (далее строим л. вл.М см. рис.)

Линия влияния поперечной силы Qk. Аналогично строится линия влияния поперечной силы алгебраической суммы сил, приложенных к отсеченной части балки относительно сечения) с рассмотрением двух положений груза. Если груз движется справа от сечения, поперечная сила равна опорной реакции А. Qk = A. (3.5) 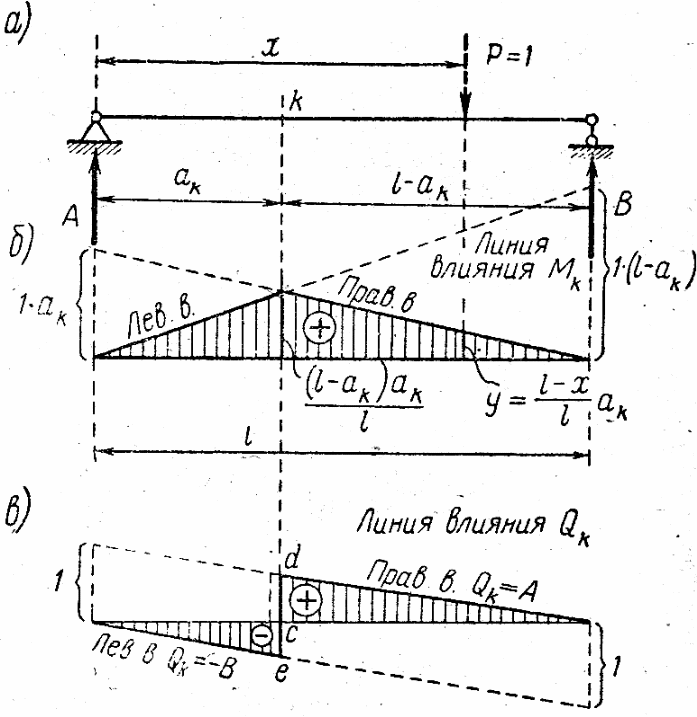Правая ветвь линии влияния Qk получается по закону изменения опорной реакции А. Этот закон справедлив, очевидно, лишь для участка изменения х от ak до l . Если груз движется слева от сечения, поперечная сила равна реакции В с обратным знаком, т. е. левая ветвь линии влияния поперечной силы получается по закону изменения правой опорной реакции В, взятой с обратным знаком. Линию (–В) используем только на участке оси балки с абсциссами от 0 до аk.(см.рис).

18.Определение усилий по линиям влияния от постоянной временной нагрузки.

Теория л. вл. позволяет определить усилия от подвиж и неподвиж нагрузок. Простейшей явл. сосредоточеная сила. Внутренние усилия : изгиб. момент от этой нагрузки опред. след. образом. М=Ру(3.1) . Если приложеная система сосред. сил , то усилие по л. вл. вычесляется: М= . (3.2).Распредиленная нагрузка: P=q*L , M=P*y=q*L* , M=q*ω(3.3), M=q*( . Усилие по л. вл. от сосред. момента опред.:Q=m* , . Выражение (3.1)-(3.5) опред. усилия от различных нагрузок . В случае если мы имеем систему различных нагрузок , усилия по л. вл. опред. следующим образом : R= (4.1), R= (4.2), R= (4.3). Если внешняя нагрузка предстовл. всеми силовыми факторами , искомая величина R опред. сумированием (4.1)-(4.3).

19. Загружение линий влияния на экстремум равномерно распределенной нагрузки. Построив линию влияния М нагружаем ее временной нагрузкой. . Расположив распред нагрузку только над полож участками находим: ; ; отриц: . Рассчитаем прочность на времен нагрузку – нормальн напряж используются в условии прочности. W – момент сопротивления.

16. Кинематический метод построения линий влияния

Кин. метод основан на принципе возможных перемещений.

Методика построения л.вл.

1. Отбрасываем опору R_B.

2. Заменяем опору реакций полож. напр.

3. Задаем полученный мех-зм возм. перемещений так, чтобы реакция совершала положительную работу. Отклоненное положение механизма есть линия в некотором масштабе.

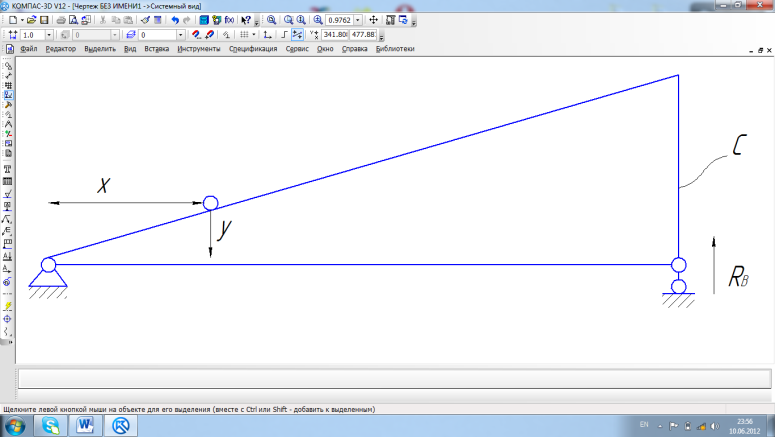
C-масштаб

при С=1 R_B=y

1. В водим в сечение 1 шарнир. Приложенный моменты положительны

Лин. вл. Q.

В ведем связь непрепятствующую верт. перем. сечений (шарнирно-стержневой паралелограм).

П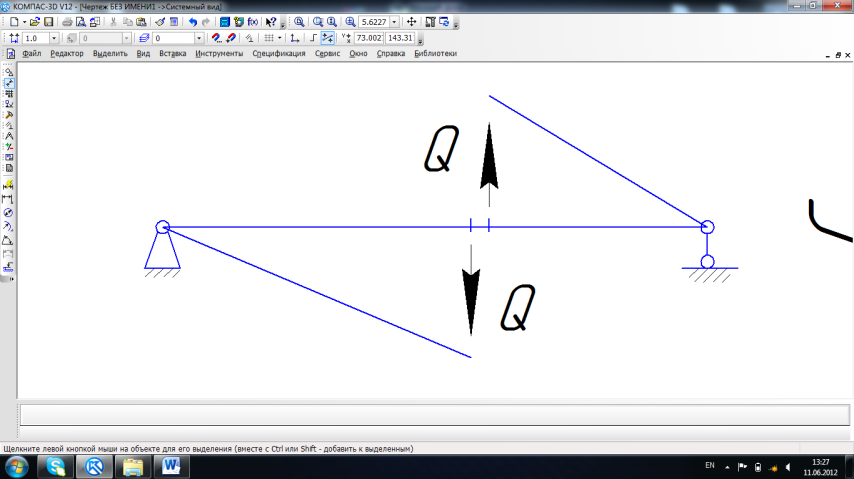 ри построении л.вл. кин. методом необходимо строго соблюдать порядок построения. Полученные ординаты имеют след. знаки: выше оси «+», ниже оси «-». Характерные ординаты л.вл. (R_A, R_B, над опорами; M и Q под рассм. сечением) опр. на осн. уравнений статики. Каждая из ординат л.вл. опр.рассматриваемую величину, когда единичный груз находится над этой ординатой.