Свойства автокорреляционных функций.

1)  равна среднему квадрату случайного процесса или математическому ожиданию квадрата
2)  Конечная ордината равна квадрату среднего значения и квадрату математического ожидания
3) Разность между начальным значением и конечным значением равна вариации процесса e(t) или дисперсия

Для центрированных процессов начальная ордината равна дисперсии.

Спектральная плотность случайного процесса

Другой важной характеристикой случайных процессов является их спектральная плотность  .

Спектральная плотность - это функция, характеризующая распределение мощности или энергии случайного процесса по частотам.

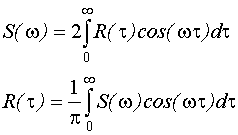
Основное свойство спектральной плотности - интеграл по всем частотам спектральной плотности, пропорциональной среднему квадрату случайного процесса.

Для центрированных процессов  есть дисперсия. Чем быстрее затухает корреляционная функция, тем шире спектральная плотность. В предельном случае, если автокорреляционная функция является  -функцией Дирака, то есть  

, то спектральная плотность постоянна во всем интервале частот  .

Сигнал, удовлетворяющий автокорреляционную функцию типа  -функции- это сигнал с бесконечно большой энергией, называемый "белым шумом".

Обобщенный метод наименьших квадратов

Недостатком метода наименьших квадратов является то, что его можно использовать при некоррелированных измерениях выхода. В случае, когда измерения выхода коррелированны, используется обобщенный метод наименьших квадратов.

Прежде чем использовать тот или иной метод, необходимо проверить, являются ли измерения выхода, используемые при обработке, коррелированными или нет.

Измерения называются коррелированными, если соответствующие им случайные величины коррелированны между собой, то есть корреляция или ковариация этих случайных величин не равна нулю.

Для определения ковариаций каждой пары измерений необходимо использовать корреляционную функцию случайного процесса e(t).

Омнк при малых выборках

Если число измерений N не велико, то  . R- это ковариационная матрица измерений размерностью (N*N), то есть квадратная матрица. является случайным вектором.

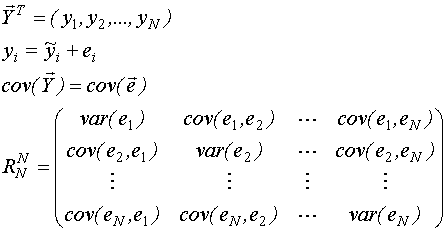
Матрицу R можно определить на основе оценки автокорреляционной функции случайного процесса e(t).

Такие оценки называются Марковскими. Они являются общим случаем оценок, частным случаем которых являются МНК оценка.

Если измерения не коррелированны между собой, то R будет иметь вид:

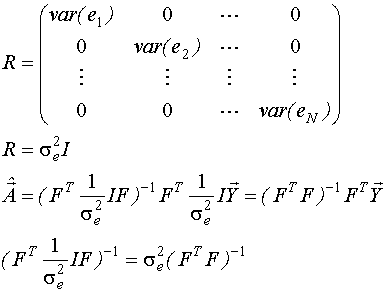
Главным недостатком Марковских оценок является обращение матрицы R, что возможно при небольшом числе измерений.  

Oмнк при большом объеме выборки

Известно, что в асимптотике (при  ) Марковские оценки стремятся к МНК оценкам, но ковариационная матрица этих оценок вычисляется по другим выражениям.

Если обращение не коррелированно, то  .

Таким образом, при большом объеме выборки (число измерений больше 100) вместо Марковских оценок можно использовать МНК оценки с преобразованной ковариационной матрицей. Это значительно проще с вычислительной точки зрения.