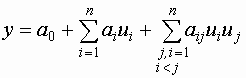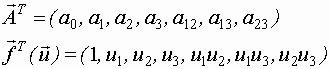Тема 18. Планирование эксперимента при наличии количественных и качественных факторов

18.1. Постановка задачи планирования эксперимента при наличии качественных факторов

18.2. Решение задач планирования с использованием совмещенных планов

18.3. Примеры совмещенных планов

18.4. Обработка информации по схеме однофакторного дисперсионного анализа

Тема 1. Введение

1.1.Типы математических моделей

1.2. Представление объекта управления в реальных условиях эксплуатации типы математических моделей

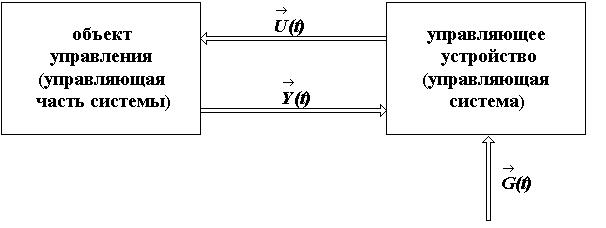
Любая система состоит из объекта управления и управляющего устройства и может быть представлена в виде следующей схемы.

- выходная координата - задающее воздействие - управляющее воздействие

Целью управления является обеспечение равенства  .

В реальных условиях объект управления подвергается воздействиям случайных помех, для обработки которых и предназначена система управления.

Целью математического моделирования является определение системы уравнений, связывающей входные и выходные переменные объекта управления. Получить такую систему уравнений можно двумя способами: аналитическим и используя экспериментально-статистические методы.

Аналитический метод предполагает изучение процессов, происходящих в объекте управления, и описание их на основе соответствующей отрасли науки. Его недостатком является невозможность качественного моделирования объектов управления, фу нкционирующих в реальных условиях.

Экспериментально-статистические методы позволяют моделировать объекты и системы, функционирующие в реальных условиях. В основе этих методов лежит эксперимент, обработка результатов которого осуществляется статистическими методами.

Экспериментально-статистические методы, как правило, предполагают, что структура математической модели известна с точностью до параметров, а основной целью этих методов является определение этих параметров.

Например.

Эксперимент заключается в измерении входных и выходных переменных. При этом эксперименты делятся на активные и пассивные.

Пассивный эксперимент заключается в измерении входных и выходных переменных в условиях нормальной эксплуатации.

Активный эксперимент заключается в изменении входных переменных по специальному плану.

Таким образом, моделирование объекта управления должно состоять из двух этапов:

1. определение структуры модели аналитическими методами; 2. определение параметров модели экспериментально - статистическими методами.

Представление объекта управления в реальных условиях эксплуатации

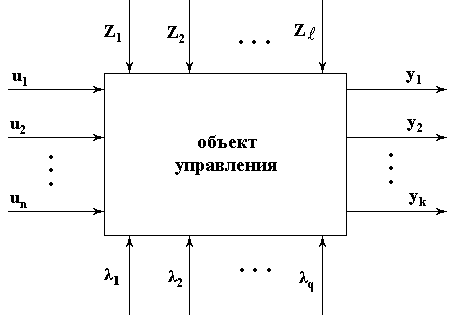
Входные переменные можно разбить на три группы:

	- вектор управляемых и контролируемых входных переменных, которые можно измерять и изменять. Через эти переменные замыкается главная обратная связь системы управления, то есть ими управляет оператор.
	- вектор неуправляемых контролируемых переменных (измеряемые и неуправляемые).
	- вектор неуправляемых и неконтролируемых выходных переменных.

 

Переменные типа  - детерминированные переменные. Переменные типа  - случайные переменные, принимающие в каждом опыте различные значения.

Математическая модель объекта управления представляет собой систему уравнений следующего вида:

Преобразование может быть определено точно, если на объект управления не действуют случайные входные переменные. При наличии переменных типа  речь идет о приближении (оценке) преобразования .

Существуют три типа преобразований:

1. функция;

2. оператор;

3. функционал.

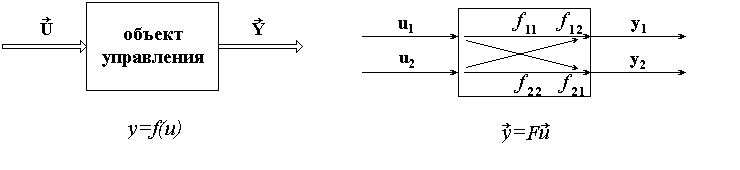
- матричная функция

Модели объектов управления делятся на модели статики (статистические) и модели динамики (динамические).

Модели статики - это уравнения связывающие выход и вход в статистическом режиме объекта управления (после окончания переходного процесса).

- коэффициент передачи.

Статическая характеристика линейных объектов линейна: 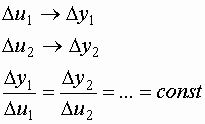 Модели статики могут быть линейно-параметризованными и нелинейно-параметризованными, то есть они могут быть линейными по неизвестным параметрам.

- линейная модель. - линейная модель с парными взаимодействиями.

Рассмотрим объект с двумя входами и одним выходом: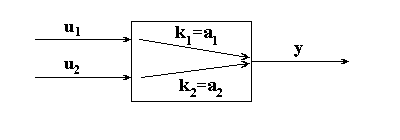

Модель 1.	, где  - свободная составляющая; - реакция на первый выход; - реакция на второй выход.
Модель 2.

Парное взаимодействие входов  и  заключается в том, что коэффициент передачи по одному входу зависит от значения другого входа.

Для проверки наличия парного взаимодействия проводят эксперимент:  

, а  будет изменяться

Если статическая характеристика по одному входу при различных значениях другого входа изменяет наклон, то взаимодействие входов имеет место, в противном случае взаимодействие отсутствует.

Для большинства объектов управления взаимодействия выше второго порядка практически равны нулю.  

Модель 3.

Рассмотрим пример, когда n=3:

- полная квадратичная модель.

Рассмотренные модели являются линейными по неизвестным параметрам. Две последние модели нелинейны по входу (по структуре).

Модель линейна по данному коэффициенту, если частная производная по нему не зависит от остальных коэффициентов.  

Линейно-параметризованная модель может быть записана в виде скалярного произведения вектора неизвестных коэффициентов и вектора-функции базисных функций:

,

где

для первой модели:
для второй модели:

Нелинейно-параметризованная модель - это модель, которую нельзя представить в виде скалярного произведения:
Модель является нелинейно-параметризованной, если хотя бы один элемент входит в нее нелинейно.	.

Тема 2. Оценивание неизвестных параметров моделей статики

2.1. Постановка задач оценивания неизвестных параметров моделей статики

2.2. Элементы теории случайных величин

2.3. Свойства оценок

2.4. Векторные случайные величины и их характеристики