Построение модели при известном значении параметра .

Предположим, что параметр  определен на основе оценки времени переходного процесса.

Если подставить оценку параметра  в линейно-комбинационную модель, то получим линейно-параметризованную модель: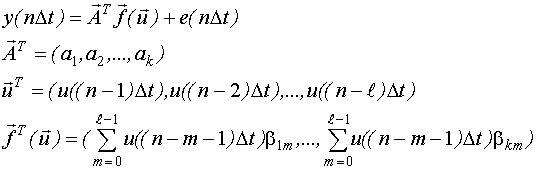

МНК-оценка вектора  имеет вид 

Введем матрицы:

Преимуществом этого метода является использование точной по структуре динамической регрессионной модели.

Если входной сигнал не является кусочно-постоянной функцией, то можно либо его аппроксимировать кусочно-постоянной функцией и использовать точную линейно-комбинационную модель, либо использовать неточную динамическую регрессионную модель соответствующую разложению импульсной переходной функции.  

Построение модели при неизвестном значении параметра .

Предположим, что параметр  неизвестен, тогда:

В случае нелинейной параметризации 

Представим модель в виде скалярного произведения:

,

но 

Для получения оценки вектора неизвестных параметров метод наименьших квадратов непригоден, необходимо использовать методы нелинейного оценивания, например, метод Гаусса-Ньютона.

В дальнейшем будем вычислять оценки вектора неизвестных параметров этим методом:

1. находим начальное приближение вектора неизвестных параметров

- МНК-оценка коэффициента разложения.

- оценка параметра затухания, полученная по времени переходного процесса.

2. разложим модель в ряд Тейлора:

Отсюда найдем первое приближение:  и так далее.

Запишем в общем виде:

- правило останова

Тема 8. Построение моделей динамики типа "вход-выход" нелинейных объектов

8.1. Модель Винера

8.2. Модель Гаммерштейна

8.3. Модель Винера-Гаммерштейна

8.4. Модель Вольтерра

8.4.1. Определение структуры модели Вольтерра. Способы представления ядер

8.4.2. Построение модели Вольтерра при известном значении параметра α

8.4.3. Построение модели Вольтерра при неизвестном значении параметра α

Нелинейные объекты управления делятся на два класса: 1. нелинейные объекты управления, допускающие каскадное представление; 2. нелинейные объекты управления, не допускающие каскадное представление. Первый класс моделей можно описать моделями Винера-Гаммерштейна, а второй класс моделями Вольтерра.    

МОДЕЛЬ ВИНЕРА

Модель Винера - последовательное соединение линейной инерционной части и нелинейной безынерционной части.

Линейную часть будем описывать в виде импульсной переходной функции. Модель нелинейной части описывается в виде отрезка степенного ряда: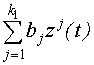 

Неизвестные параметры модели Винера:  .

Кроме этих параметров в число неизвестных параметров модели Винера необходимо включить постоянную составляющую выходного сигнала:

- число неизвестных параметров в модели Винера.

Необходимость введения в модель постоянной составляющей вызвана невыполнением принципа суперпозиции для нелинейных систем.  

Таким образом, нелинейная система должна связывать истинные значения выхода и входа.

   

После представления линейной и нелинейной частей каскадной модели необходимо определить структуру соответствующей динамической регрессионной модели, в данном случае - модели Винера.

Получим структуру этой модели в предположении, что входной сигнал является кусочно-постоянной функцией времени:

Если запишем в виде  , то получим линейно-комбинационную модель Винера.

Полученная модель существенно нелинейна по всем неизвестным параметрам, кроме постоянной составляющей выходного сигнала, поэтому оценивание неизвестных параметров этой модели возможно только нелинейными методами.

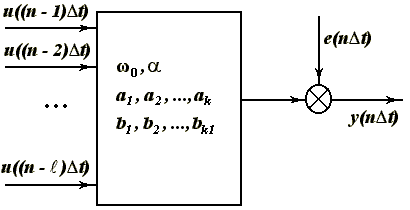
Оценивание вектора неизвестных параметров производится по тем же формулам что и для линейного объекта при подстановке в них вектора-функции частных производных

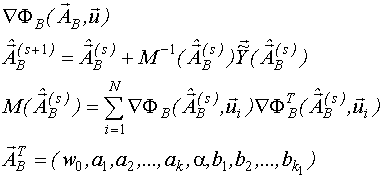
Берем производную по  , потом по  , по  и так далее.

Начальное приближение вектора неизвестных параметров  , в отличиe от начального приближения вектора неизвестных параметров  , оценить достаточно сложно. Обычно приближение задается произвольно, что усложняет процедуру.    

МОДЕЛЬ ГАММЕРШТЕЙНА

Модель Гаммерштейна - последовательное соединение нелинейной безинерционной части и линейной инерционной части.

Получим выражение для случая кусочно-постоянного входного сигнала в дискретной форме.

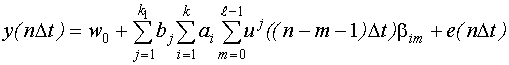
Модель Гаммерштейна содержит те же параметры что и модель Винера, но структура модели другая. Она линейна только по  , по  .

Получим выражение для вектора функции  , причем  .

МОДЕЛЬ ВИНЕРА-ГАММЕРШТЕЙНА

Модель Винера-Гаммерштейна - последовательное соединение двух линейных инерционных частей разделенных одной нелинейной безинерционной частью.

   

МОДЕЛЬ ВОЛЬТЕРРА Определение структуры модели Вольтерра. Способы представления ядер.

Определение структуры модели Вольтерра. Способы представления ядер. Модели Вольтерра - наиболее общий класс моделей нелинейных систем, частным случаем моделей Вольтера являются модели Винера и Винера-Гаммерштейна. Модель Вольтерра - модель основанная на функционально-степенном ряду Вольтерра. В частности, модель Вольтерра является трехчленным отрезком ряда Вольтерра. Ряд Вольтерра имеет вид:

В общем виде:

В задачах идентификации используется трехчленный отрезок ряда Вольтерра, то есть выражение вида: , где  - ядро Вольтерра первого порядка; - ядро Вольтерра второго порядка; - ядро Вольтерра нулевого порядка или постоянная составляющая.

Обычно ядра представлены в виде разложения по базисным функциям (чаще всего используются функции Лагерра). Представление ядер в виде ординат импульсной переходной функции обычно не используется, так как ему соответствует слишком большой вектор неизвестных параметров. Будем представлять ядро первого порядка:

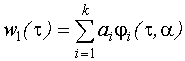
Ядро второго порядка:

Это сепарабельное представление, то есть функция двух аргументов представлена в виде произведения двух функций одного аргумента.

Получим дискретную регрессионную модель Вольтерра вида:

Вектор неизвестных параметров:

- число неизвестных параметров.

Данная модель нелинейно-параметризованная, но если известен параметр  , то модель линейно-параметризованная, следовательно, возможны два метода вычисления оценок вектора неизвестных параметров:

1- метод наименьших квадратов, если параметр  определен из оценки времени переходного процесса;

2- метод, основанный на нелинейном оценивании вектора неизвестных параметров.    

Построение модели Вольтерра при известном значении параметра .

Метод построения модели Вольтерра при известном значении параметра  основан на оценивании вектора  .

   

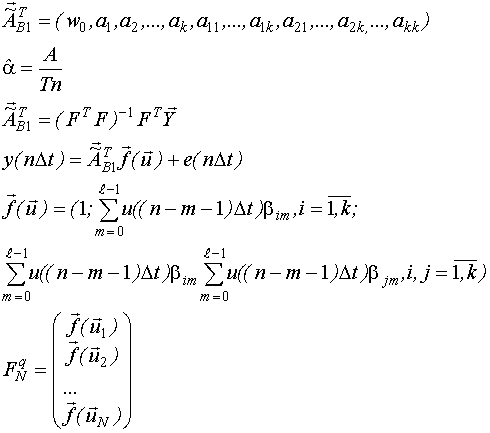
Построение модели Вольтерра при неизвестном значении параметра .

Построение модели Вольтерра при неизвестном значении параметра  предполагает оценивание всего вектора неизвестных параметров В качестве начального приближения вектора неизвестных параметров используют следующий вектор:

Модель Вольтерра - это обобщенная модель нелинейной системы, частным случаем которой является модель Винера. Покажем, что при  модель Винера является частным случаем трехчленного отрезка ряда Вольтерра:

Если  , то модель Винера совпадает с моделью Вольтерра. Модель Винера-Гаммерштейна так же является частным случаем модели Вольтерра.

Тема 9. Модели пространства состояний

9.1. Понятие моделей пространства состояний

9.2. Непрерывная форма модели пространства состояний

9.3. Дискретная модель пространства состояний

9.4. Приведение модели пространства состояний к динамической регрессионной модели типа "вход-выход"

9.5. Соотношения между элементами вектора неизвестных параметров и ординатами импульсной переходной функции

9.6. Вычисление НМНК-оценок элементов вектора неизвестных параметров

9.7. Построение моделей пространства состояний с внутренним шумом

9.8. Алгоритм совместного оценивания элементов векторов и

ПОНЯТИЕ МОДЕЛЕЙ ПРОСТРАНСТВА СОСТОЯНИЙ.

Модель пространства состояний - динамическая модель, которая связывает между собой три группы переменных:

1. входные переменные объекта управления;

2. переменные состояния объекта управления;

3. выходные переменные объекта управления.

Переменные состояния объекта управления - это дополнительные переменные, использование которых позволяет зависимость не только выходной переменной от входной, но и некоторые функции выходной переменной от входной.

Число переменных состояния равно порядку дифференциального уравнения описывающего объект управления.

Частным случаем переменных состояния являются фазовые координаты, то есть производные выходного сигнала.

- вектор состояния или вектор фазовых переменных.

В дальнейшем будем рассматривать дискретные модели пространства состояний.

   

НЕПРЕРЫВНАЯ ФОРМА МОДЕЛИ ПРОСТРАНСТВА СОСТОЯНИЙ.

В непрерывной форме модель пространства состояний в общем случае и имеет вид:

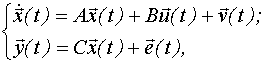
где  - k-мерный вектор входных воздействий;

-  -мерный вектор выходных воздействий;

- n-мерный вектор пространства состояний;

-  -мерный вектор внешнего шума;

- n-мерный вектор внутреннего шума;

- матрица состояний;

- матрица управления;

- матрица наблюдений.    

ДИСКРЕТНАЯ МОДЕЛЬ ПРОСТРАНСТВА СОСТОЯНИЙ.

В дальнейшем будем использовать дискретные модели пространства состояний, которые для одномерных систем имеют вид:

- уравнение состояния,

- уравнение наблюдения,

где  - матрица состояний;

- n-мерный вектор управления;

- n-мерный вектор наблюдений;

k - дискретное время.

В дискретной модели роль первой производной выполняет первая разность  .

Аналогом второй производной является вторая разность

.

Если переменными состояния являются фазовые координаты, товектор наблюдений  имеет вид:

.

В этом случае неизвестными параметрами являются матрица T и вектор  , число неизвестных параметров:  .

Чтобы уменьшить число неизвестных параметров обычно используется каноническая форма модели пространства состояний. В соответствии с этой формой T имеет вид:

Каноническая структура содержит 2n неизвестных параметров. Вектор неизвестных параметров 

 ПРИВЕДЕНИЕ МОДЕЛИ ПРОСТРАНСТВА СОСТОЯНИЙ К ДИНАМИЧЕСКОЙ РЕГРЕССИОННОЙ МОДЕЛИ ТИПА "ВХОД-ВЫХОД".

Если начальные условия объекта управления нулевые, то есть при  , то модель пространства состояний может быть сведена к динамической регрессионной модели типа ⌠вход √ выход■.

Поскольку все реальные объекты функционируют не при нулевых начальных условиях, то при их описании динамическими регрессионными моделями необходимо в качестве переменных использовать их отклонения от исходного статического состояния, то есть состояния, в котором находится объект до начала его исследования. При этом необходимо, чтобы до начала исследований объект управления находился в статическом состоянии хотя бы в течение времени памяти объекта управления, то есть переменные должны быть постоянными.

Выведем структуру динамической регрессионной модели эквивалентной модели пространства состояний при нулевых начальных условиях:

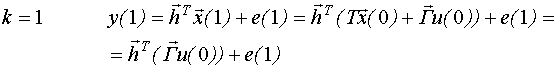
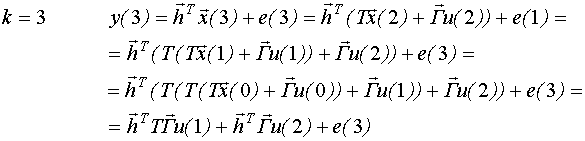
Таким образом, мы получили модель типа ⌠вход-выход■, которую можно записать следующим образом:

- дискретная модель свертки,

где  - i-ая ордината импульсной переходной функции, определяемая следующим матричным выражением:  .

i-ая ордината импульсной переходной функции однозначно определяется значениями параметров матрицыT и вектора  модели пространствасостояний, то есть она является функцией вектора  и является сильно нелинейной.

Таким образом, получена модель типа ⌠вход √ выход■, неизвестными параметрами которой являются неизвестные параметры модели пространства состояний. Получив такую модель по изменениям входа и выхода, мы получим искомую модель пространства состояний.

Полученная структура динамической регрессионной модели является нелинейно-параметризованной по всем неизвестным параметрам.    

СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ВЕКТОРА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ  И ОРДИНАТАМИ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИИ.

Для получения оценки вектора неизвестных параметров необходимо использовать методы нелинейного оценивания. При нахождении начального приближения необходимо использовать соответствия между элементами вектора  и ординатами импульсной переходной функции, таким образом, процедура нелинейного оценивания должна реализовываться в следующей последовательности:

1. определение методом наименьших квадратов оценок ординат импульсной переходной функции;

2. вычисление неизвестных коэффициентов модели пространства состояний по оценкам ординат импульсной переходной функции с использованием соответствующих соответствий, найденные оценки принимаются в качестве начальной оценки вектора  ;

3. нахождение НМНК-оценки вектора неизвестных параметров методом Гаусса-Ньютона.

Такой подход позволяет обеспечить достаточно высокую точность начального приближения вектора неизвестных параметров, что необходимо для обеспечения сходимости метода Гаусса-Ньютона, и уточнить структуру модели пространства состояний (порядок системы) после решения первого этапа по виду импульсной переходной функции.

Получим соответствие между элементами вектора неизвестных параметров и ординатами импульсной переходной функции:

Таким образом, первые n ординат импульсной переходной функции равны

соответствующим элементам вектора  .

(1)

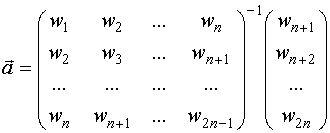(2)

Использование полученных соотношений (1) и (2) корректно только в части вычисления оценок вектора  . Точность оценок матрицы  зависит от оценки вектора  . Если ординаты импульсной переходной функции вычислены неточно, то задача может стать некорректной, что следует из необходимости обращения матрицы  , которая может быть плохо обусловлена. Поэтому это соответствие можно использовать либо в детерминированном случае, либо при вычислении начального приближения вектора неизвестных параметров  в задаче нелинейного оценивания.

ВЫЧИСЛЕНИЕ НМНК-ОЦЕНОК ЭЛЕМЕНТОВ ВЕКТОРА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ 

Разложим функцию регрессии в ряд Тейлора в окрестностях точки 

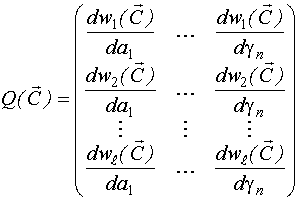
Матрица  может быть вычислена по общему алгоритму.

Пусть n=2

I  строка 0 0 1 0

II строка 0 0 1 0

Первые n строк матрицы  представляют собой блочную матрицу, состоящую из двух квадратных матриц размерностью n*n:

где  - нулевая матрица;

- единичная матрица.

Найдем n+1 строку

III строка 

IV строка 

Тогда, в общем виде:

НМНК-оценка вектора неизвестных параметров вычисляется методом Гаусса-Нъютона по следующей итерационной формуле:

   

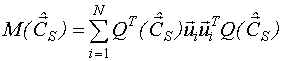
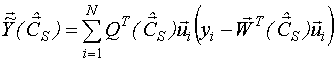
ПОСТРОЕНИЕ МОДЕЛЕЙ ПРСТРАНСТВА СОСТОЯНИЙ С ВНУТРЕННИМ ШУМОМ.

Рассмотрим одномерную дискретную систему, описываемую моделью пространства состояний вида

где  - вектор неизвестных параметров;

- дискретный внутренний шум системы.

В этом случае неизвестны элементы векторов  и  .

Модель пространства состояний с внутренним шумом при нулевых начальных условиях также можно свести к динамической регрессионной модели типа ⌠вход-выход■.  

,

,

где  - вектор ординат импульсной переходной функции по каналу внутренний шум - выход;

- дискретное время памяти по каналу внутренний шум - выход;

- вектор предыстории по внутреннему шуму.

Поскольку внутренний шум не может быть измерен, полученную модель ⌠вход - выход■ непосредственно для оценивания векторов  и  использоватьнельзя. Для оценивания параметров модели пространства состояний с внутренним шумом можно использовать следующий подход:

Обозначим  , с учетом того, что  и e(k) являются случайными функциями времени, их можно объединить в  . Представим процесс  как выход некоторой линейной динамической системы, на вход которой подается чисто случайный процесс  - белый шум.

Таким образом, при таком представлении модели, ее неизвестными параметрами являются элементы вектора  и неизвестные параметры фильтра, преобразующего ⌠белый шум■ в процесс  . При этом, обычно модель фильтра задают в виде его дискретной передаточной функции , структура которой задается априори.

,

где z √ оператор сдвига на число разрядов дискретного времени, равное степени z, то есть 

Таким образом, задача свелась к задаче оценивания вектора  и неизвестных коэффициентов дискретной передаточной функции.

Окончательно мы получили вектор неизвестных параметров

Модель  обычно представляется следующим образом:

Умножим левую и правую часть на и получим:

где  - отфильтрованное значение выхода;

- отфильтрованный вектор предыстории по входу.

Таким образом, относительно отфильтрованных значений полученная модель совпадает с моделью без внутреннего шума, при условии, что внешний шум является белым шумом.

АЛГОРИТМ СОВМЕСТНОГО ОЦЕНИВАНИЯ ЭЛЕМЕНТОВ ВЕКТОРОВ  И  .

Алгоритм является итерационным и реализуется в следующей последовательности:

1. На основе результатов эксперимента (то есть измерений значений входных и выходных переменных) вычисляется НМНК - оценка вектора  без учета внутреннего шума.

2. Вычисляется вектор невязок

- вектор отклонений экспериментальных значений от нашей модели. При этом принимается полученное значение невязок в качестве оценок  .

3. Методом наименьших квадратов вычисляется начальная оценка вектора параметров фильтра .

4. Фильтрация значений входных  и выходных  переменных:

5. Вычисление НМНК - оценки вектора по процедуре Гаусса-Ньютона с заменой значений входных и выходных переменных на отфильтрованные.

6. Вычисление  и так далее.

Процедура заканчивается тогда, когда  (- заданное малое число).

Тема 10. Основы теории планирования эксперимента

10.1. Основные идеи планирования эксперимента

10.2. Основные понятия и определения теории планирования эксперимента

10.2.1. Факторы планирования

10.2.2. Пространство планирования

10.2.3. План эксперимента

10.2.4. Критерии оптимальности планов и моделей

ОСНОВНЫЕ ИДЕИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.

Пусть имеется объект,

структура модели которого является линейно-параметризованной.

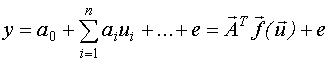
МНК-оценка вектора неизвестных коэфициентов:

Качество модели характеризуется ковариационной матрицей  .

В случае линейной параметризации модели информационная матрица определяется на основе измерений входных переменных объекта (то есть информационная матрица определяется матрицей входных переменных ) и не зависит от значений выхода, полученных по результатам эксперимента.

В случае линейной параметризации модели имеется возможность так спланировать эксперимент, то есть определить такую матрицу входных переменных, при которой ковариационная матрица оценок неизвестных параметров обладает теми или иными желаемыми свойствами. В пассивном эксперименте, когда матрица входных переменных является во многом случайной, ковариационная матрица оценок чаще всего является плохо обусловленной (то есть ее детерминант близок к нулю), поэтому планирование эксперимента, то есть активное экспериментирование, когда входные переменные не просто измеряются, а устанавливаются на некоторых оптимальных уровнях, позволяет получить модели, обладающие теми или иными оптимальными свойствами.    

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

ТЕОРИИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.

Факторы планирования.

Факторами планирования будем называть управляемые входные переменные

Пространство планирования.

Пространство планирования  - это область в n-мерном пространстве, внутри и на границах которой можно проводить опыты. Область планирования может быть правильной и произвольной формы.    

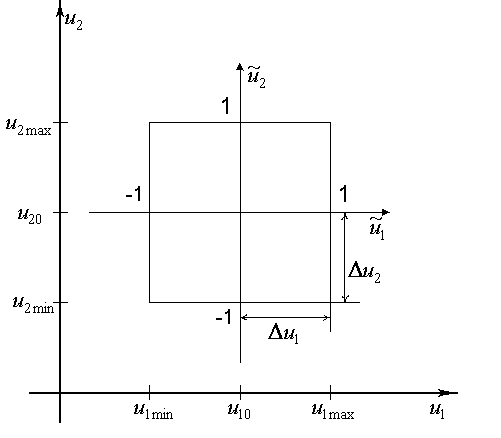
Обычно факторы планирования нормируют следующим образом:

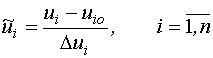
- координата центра области планирования;

- половина интервала планирования.

Нормированное пространство планирования (пространство планирования для нормированных факторов) представляет собой единичный n-мерный гиперкуб.

На этапе планирования эксперимента обычно используются нормированные факторы, а на этапе обработки результатов эксперимента вначале получают модель для нормированных факторов, а затем осуществляют переход к исходным факторам путем замены нормированных факторов их выражениями.

Большинство известных планов предполагают, что областью планирования являются либо единичный n-мерный гиперкуб, либо единичная гиперсфера.

План эксперимента.

План эксперимента ( ) - это совокупность точек пространства планирования, в которых производятся опыты. План эксперимента задается спектром плана и частотами повторений наблюдений в точках спектра.

Спектр ("скелет плана") - это совокупность неповторяющихся точек пространства планирования, в которых производятся опыты.

Частота повторения наблюдений в i-ой точке определяется:

,

где  - число опытов в i-ой точке спектра;

- общее число опытов, предусмотренных планом;

Планы делятся на точные и непрерывные.

План называется точным, если в нем все точно известно, то есть общее число опытов и число опытов в i-ой точке плана известны и являются целымивеличинами.

План называется непрерывным или асимптотическим, если для заданного значения общего числа опытов не все значения числа опытов в i-ой точке являются целыми величинами. Если для данного значения числа опытов план не является точным, то его необходимо округлить до ближайшего точного плана при том же общем числе опытов, либо изменить общее число опытов.

Критерии оптимальности планов и моделей.

Каждый план и полученная на его основе регрессионная модель должны удовлетворять соответствующему критерию оптимальности.

Критерии оптимальности делятся на две группы. К первой группе относятся критерии, характеризующие точность оценок неизвестных параметров модели; ко второй √ критерии, характеризующие предсказательные свойства, полученной на основе плана модели регрессии.

Первая группа:

1) критерий ортогональности,

2) D-оптимальность,

3) A-оптимальность и т.д.

Вторая группа:

1) рототабельность,

2) G-оптимальность,

3) Q-оптимальность и т.д.

Критерий ортогональности.

План называется ортогональным, если соответствующая ему ковариационная матрица оценок параметров модели диагональная:

Ортогональный план обеспечивает некоррелированность МНК - оценок неизвестных параметров модели.

D-оптимальность.

План называется D-оптимальным, если он минимизирует определитель ковариационной матрицы оценок, то есть:

Критерий D-оптимальности обеспечивает минимизацию объема эллипсоида рассеивания оценок параметров модели или обобщенную дисперсию оценок.

Пусть имеется модель 

В результате многократного повторения идентификации получим точки, попадающие в область, ограниченную эллипсом рассеивания.

Внутри эллипса находится точка с координатами равными истинным значениям неизвестных параметров модели.

Объем эллипсоида рассеивания прямо пропорционален определителю ковариационной матрицы.

А-оптимальность.

План называется А-оптимальным, если он минимизирует след ковариационной матрицы оценок неизвестных параметров

Этот критерий минимизирует сумму дисперсий оценок неизвестных параметров.

Недостаток данного критерия состоит в том, что он не учитывает коррелированность оценок неизвестных параметров.

Вторую группу критериев оптимальности составляют критерии, обеспечивающие те или иные свойства дисперсионной функции регрессионной модели, то есть функции, определяющей зависимость дисперсии предсказания выхода по модели от координат точки предсказания.

- дисперсионная функция

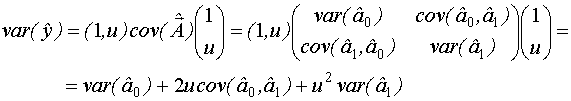
Рототабельность.

План называется рототабельным, если дисперсия предсказания выхода по соответствующей ему модели зависит только от расстояния точки предсказания от центра области планирования и не зависит от направления предсказания, то есть в точках равноудаленных от центра области планирования дисперсия предсказания одинакова.

Критерий рототабельности удобен, если получаемая регрессионная модель используется при статической оптимизации параметров или режимов объектов. При этом предполагается, что оптимизация осуществляется поисковыми методами.

G-оптимальность.

План называется G-оптимальным или минимаксным, если он минимизирует максимальную по пространству планирования дисперсию предсказания выхода.

Максимальная дисперсия должна быть минимальна по пространству планирования.

Существует теорема эквивалентности, согласно которой для линейно-параметризованных моделей критерии D- и G-оптимальности эквивалентны. То есть D-оптимальный план является G-оптимальным инаоборот.

Q-оптимальность.

План называется Q-оптимальным, если он минимизирует среднюю по пространству планирования дисперсию предсказания выхода.

Тема 11. Ортогональные планы первого порядка

11.1. Назначение и типы ортогональных планов первого порядка

11.2. Полный факторный эксперимент (ПФЭ, )

11.3. Вычисление МНК-оценок и их свойства при ортогональном планировании первого порядка.

11.4. Статистический анализ регрессионной модели.

НАЗНАЧЕНИЕ И ТИПЫ

ОРТОГОНАЛЬНЫХ ПЛАНОВ ПЕРВОГО ПОРЯДКА.

Назначение ортогональных планов первого порядка - построение линейных моделей статики вида:

Существуют два типа ортогональных планов первого порядка:

1. Полный факторный эксперимент (ПФЭ,  ). 2. Дробный факторный эксперимент (ДФЭ,  ).    

ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ.

Полным факторным экспериментом называется точный план, спектр которого включает по одному разу все вершины пространства планирования типа единичный n-мерный гиперкуб, а частоты повторений наблюдений во всех точках спектра одинаковы и равны:

+1	+1
-1	+1	Спектр плана
+1	-1
-1	-1

Полный факторный эксперимент является точным планом только для числа опытов, кратных 2^n.  

+1	+1	+1
-1	+1	+1
+1	-1	+1
-1	-1	+1
+1	+1	-1
-1	+1	-1
+1	-1	-1
-1	-1	-1

Матрица полного факторного эксперимента записывается следующим образом: в первом столбце знаки ⌠+■ и ⌠-■ меняются на каждой строке, в каждом последующем столбце частота смены знаков уменьшается в два раза по сравнению с предыдущим столбцом. В последнем столбце первая половина имеет знак ⌠+■, а вторая половина √ знак ⌠-■.

Реализация полного факторного эксперимента осуществляется в случайной последовательности. Прежде чем приступить к реализации опытов, необходимо произвести рандомизацию матрицы плана (определить случайную последовательность строк матрицы плана).  

			Серия
			1	2	3
+1	+1	+1	3	4	8
-1	+1	+1	7	8	1
+1	-1	+1	1	3	5
-1	-1	+1	8	7	6
+1	+1	-1	4	6	7
-1	+1	-1	6	5	2
+1	-1	-1	5	2	4
-1	-1	-1	2	1	3

Рандомизация осуществляется на основе таблицы случайных чисел, из которой извлекаются элементы из интервала от 1 до N. Рандомизация необходима для защиты результатов эксперимента от возмущений, действующих на объект, и при построении модели используют усредненное значение выхода по всем сериям.

Реализация плана на объекте производится в случайной последовательности, в результате которой получается матрица значений выхода ,где N - число опытов, m - число повторений плана (m=3 - 5).

,

- значение выхода объекта в i-ом опыте j-ой серии.

После проведения эксперимента необходимо вычислить МНК - оценки неизвестных параметров модели и провести статистический анализ полученной регрессионной модели.

ВЫЧИСЛЕНИЕ МНК-ОЦЕНОК И ИХ СВОЙСТВА ПРИ ОРТОГОНАЛЬНОМ ПЛАНИРОВАНИИ ПЕРВОГО ПОРЯДКА

При вычислении МНК-оценок используются усредненные значения выхода:

Рассмотрим пример при N=3

Матрица полного факторного эксперимента обладает следующими тремя свойствами:

1. Сумма элементов любого столбца равна нулю:

2. Сумма квадратов элементов любого столбца равна числу опытов:

3. Скалярное произведение каждой пары столбцов равно нулю:

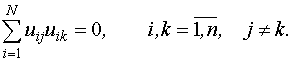
Матрица базисных функций, соответствующая полному факторному эксперименту, также обладает этими свойствами, за исключением первого столбца, для которого не выполняется первое свойство.

Информационная матрица полного факторного эксперимента диагональная, так как в соответствии со вторым свойством все диагональные элементы информационной матрицы равны N, а в соответствии с третьим свойством все недиагональные элементы равны нулю.

Таким образом, оценка i-го элемента вектора  равна алгебраической сумме элементов вектора  с учетом знаков элементов i-го столбца матрицы базисных функций F, деленной на N.

Ковариационная матрица МНК - оценок равна

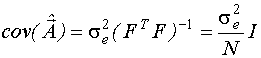
Таким образом, при ортогональном планировании первого порядка дисперсии оценок всех коэффициентов модели одинаковы и равны  , а ковариации каждой пары равны нулю.    

СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕГРЕССИОННОЙ МОДЕЛИ

Статистический анализ при активном экспериментировании начинается с проверки гипотезы о воспроизводимости результатов эксперимента. Эта гипотеза формулируется следующим образом: эксперимент является воспроизводимым, если в каждой точке плана генеральная дисперсия выхода одинакова.

Таким образом, воспроизводимость может иметь место только тогда, когда случайный процесс e(t) является стационарным процессом.

Дисперсии в точках плана можно оценить на основе матрицы значений выхода.

- построчные дисперсии.

Проверка гипотезы воспроизводимости осуществляется на основе критерия Кохрена (G-распределения).

Если выполняется неравенство  , то эксперимент признается воспроизводимым. Если эксперимент признан воспроизводимым, то в качестве оценки дисперсии внешнего шума принимается среднеарифметическое значение всех построчных дисперсий.

Остальные этапы статистического анализа (проверка значимости оценок, проверка адекватности и расчет доверительных интервалов) производятся аналогично случаю пассивного эксперимента с использованием в качестве оценки дисперсии внешнего шума среднеарифметического значения построчных дисперсий с числом степеней свободы равным N(m-1). Таким образом, в случае активного эксперимента отпадает необходимость проведения дополнительного эксперимента с целью определения оценки внешнего шума, которая определяется по результатам активного эксперимента.

В случае, если эксперимент невоспроизводим, то есть дисперсии в разных точках неодинаковы, то можно использовать специальные планы для построения которых необходима функция эффективности эксперимента  , то есть зависимость дисперсии внешнего шума от координат точек плана.

В качестве функции эффективности можно использовать функцию, значения которой равны построчным дисперсиям.

Основным недостатком полного факторного эксперимента является его сильная избыточность, особенно при большом числе факторов. Поэтому полный факторный эксперимент применим для сравнительно небольшого числа факторов. При большом числе факторов необходимо использовать дробный факторный эксперимент, который позволяет резко сократить число опытов, то есть обладает большей насыщенностью.

Тема 12. Дробный факторный эксперимент

12.1. Назначение дробного факторного эксперимента

12.2. Полуреплики

12.3. Четвертьреплики

НАЗНАЧЕНИЕ ДРОБНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА

Дробный факторный эксперимент предназначен для построения тех же моделей, что и полный факторный эксперимент:

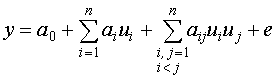
При дробном факторном эксперименте факторы делятся на две группы: основные и вспомогательные (дополнительные). При этом число вспомогательных факторов -  , основных - (n-), число опытов -  . Если  =1, то план называется полурепликой от полного факторного эксперимента, если =2 √ 1/4 репликой, если =3 √ 1/8 репликой и так далее.    

ПОЛУРЕПЛИКИ

Полуреплика √ это половина полного факторного эксперимента.

Рассмотрим пример при числе факторов n=3

-основные факторы.

- вспомогательный фактор.

Для построения матрицы дробного факторного эксперимента необходимо задать генерирующие соотношения (ГС), то есть определить, какому произведению основных факторов соответствует дополнительный фактор.

В дробном факторном эксперименте факторы всегда изменяются по плану полного факторного эксперимента типа  , где m=n-.  

u1	u2	u3
+1	+1	+1
-1	+1	-1
+1	-1	-1
-1	-1	+1

Матрица плана дробного факторного эксперимента обладает теми же свойствами, что и матрица полного факторного эксперимента. Матрица базисных функций, соответствующая дробному факторному эксперименту, так же удовлетворяет тем же свойствам, за исключением первого столбца, для которого не выполняется первое свойство.

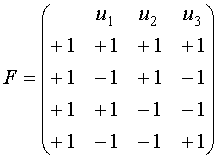
Вычисление оценок неизвестных коэффициентов модели производится по тем же формулам, что и для полного факторного эксперимента:

Таким образом, для дробного факторного эксперимента возникает явление смешивания оценок, то есть каждая алгебраическая сумма измерений выхода, деленная на число опытов, оценивает несколько истинных коэффициентов модели (в рассматриваемом случае два коэффициента - ).

Для определения так называемой разрешающей способности дробного факторного эксперимента строится таблица смешивания оценок:

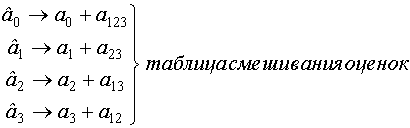
Она определяет разрешающую способность ДФЭ.

Прежде чем разбить факторы на основные и дополнительные нужно иметь априорную информацию о наличии взаимодействия факторов. Имея таблицу смешивания, можно на основании априорной информации разбить факторы. Таблицу легко получить на основе определяющего контраста (ОК) √ выражения, получаемого на основе генерирующего соотношения. Определяющий контраст получается путем умножения левой и правой части генерирующего соотношения на левую часть.

Таблица смешивания коэффициентов получается следующим образом: каждая алгебраическая сумма является оценкой соответствующего коэффициента модели и коэффициента, который соответствует произведению факторов, получаемому при умножении правой части определяющего контраста на фактор, соответствующий алгебраической сумме.

В общем случае полуреплика пригодна лишь для построения линейных моделей без парных взаимодействий.    

ЧЕТВЕРТЬРЕПЛИКИ

Рассмотрим пример при числе факторов n=5.

- основные факторы,

- вспомогательные факторы.

Для реплик высокой степени дробности вводится понятие обобщенного определяющего контраста (ООК), который получается из определяющих контрастов для всех дополнительных факторов.

Обобщенный определяющий контраст определяется путем приравнивания единице правых частей определяющих контрастов для всех дополнительных факторов и всевозможных их произведений.

Для 1/8 реплики в правой части ООК будет семь произведений факторов.

Наилучшей разрешающей способностью обладают те реплики, которые в качестве генерирующих соотношений используют произведения всех основных факторов. Анализ разрешающей способности реплик лучше проводить с помощью ЭВМ, используя пакет ⌠ПЛАНЭКС■.

Планы полного и дробного факторных экспериментов могут быть использованы для решения задач статической оптимизации объектов, подверженных действию случайных возмущений и помех.

Тема 13. Метод Бокса-Уилсона. Планирование второго порядка

13.1. Идея метода Бокса-Уилсона

13.2. Пример реализации метода Бокса-Уилсона

13.3. Назначение и типы планов второго порядка

13.4. Полный факторный эксперимент типа

13.5. Композиционные планы (ОЦКП, РЦКП)

13.6. ОЦКП

13.7. Вычисление МНК-оценок неизвестных параметров. Определение дисперсий оценок

13.8. РЦКП

ИДЕЯ МЕТОДА БОКСА-УИЛСОНА

Задача статической оптимизации сводится к определению таких значений входных параметров, при которых выход объекта принимает экстремальное значение.

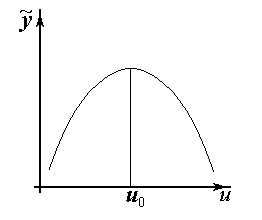
Метод Бокса-Уилсона представляет собой совокупность метода крутого восхождения и методов планирования экспериментов. Он основан на понятии градиента.

Градиент - это вектор, направленный в сторону максимально быстрого возрастания функции

,

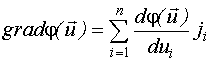где  - единичная орта, направленная вдоль i-ой оси

Метод Бокса-Уилсона ортогональные планы первого порядка реализует на каждом цикле крутого восхождения, при этом исходная точка каждого цикла принимается центром области планирования. Задается область планирования, по результатам реализации плана оценивается направление градиента и осуществляется движение вдоль этого направления. Процесс оптимизации заканчивается на том цикле, в начале которого все компоненты вектора градиента статистически незначимы.

Задаем начальную точку  и область планирования . Проводим полный факторный эксперимент. Находим  .

Первый цикл крутого восхождения начинается с точки, соответствующей центру исходной области планирования. Из этой точки начинается движение в сторону градиента, при этом чередуются мысленные и реализуемые опыты.

Мысленный опыт - опыт, не реализуемый на объекте и заключающийся лишь в переходе от одной точки, расположенной в направлении градиента, к другой. Опыт сводится к пересчету координат. Для пересчета необходимо знать шаг движения по градиенту.

Реализуемый опыт √ это опыт, который производится в соответствующей точке, расположенной на направлении градиента.

Первый цикл крутого восхождения заканчивается на том реализуемом опыте, которому соответствует максимальное значение выхода. Эта точка принимается в качестве центра области планирования для оценки направления градиента для второго цикла.

После оценки параметров модели на каждом цикле необходимо проверить их статистическую значимость с тем, чтобы определить является ли предыдущий планируемый цикл завершением процедуры оптимизации.    

ПРИМЕР РЕАЛИЗАЦИИ МЕТОДА БОКСА-УИЛСОНА.

Факторы	Хром Cr	Никель Ni	Молибден Mo	Ванадий V	Ниобий Nb	Марганец Mn	Углерод C
Основ.уровни,% Интервал варьирования,% Верхний +1 Нижний √1	4 1 5 3	2 1 3 1	0,1 0,1 0,2 0	0,02 0,02 0,04 0	0,1 0,1 0,2 0	0,4 0,1 0,5 0,3	0,4 0,1 0,5 0,3	Сопротивление на разрыв при t=800╟С
- реплики	-1 +1 +1 -1 +1 -1 -1 +1	-1 +1 -1 +1 -1 +1 -1 +1	-1 -1 +1 +1 -1 -1 +1 +1	-1 -1 -1 -1 +1 +1 +1 +1	-1 +1 +1 -1 -1 +1 +1 -1	-1 +1 -1 +1 +1 -1 +1 -1	-1 -1 +1 +1 +1 +1 -1 -1	4,5 3,5 6,2 3,2 5,3 5,1 5,3 5,8
(МНК)  Шаг движения по  Округл. шаг	0,71     0,71 0,8	-0,09     -0,09 -0,1	0,65     0,064 0,07	0,89     0,018 0,02	0,54     0,054 0,06	0,16     -0,016 -0,02	0,46     0,04 0,05
Мысленные 1 опыты 2 3 4	4,8     7,2	1,9     1,6	0,17     0,38	0,04     0,1	0,16     0,34	-0,38     -0,32	0,45     0,6
Реализованный опыт 9 Мысленный опыт 5 Реализованный  опыт 10 11 12 13	8,0 8,8 9,6 10,4 11,2 12,0	1,5 1,4 1,3 1,2 1,1 1,0	0,45 0,52 0,59 0,66 0,73 0,80	0,12 0,44 0,16 0,18 0,2 0,22	0,4 0,46 0,52 0,58 0,64 0,70	0,3 0,28 0,26 0,24 0,22 0,2	0,65 0,7 0,75 0,80 0,85 0,9	10,3         11,0 11,5 11,2 10,1

Округления производятся таким образом, чтобы соответствующие исходным и округленным значениям вектора мало отличались друг от друга по направлению.

НАЗНАЧЕНИЕ И ТИПЫ ПЛАНОВ ВТОРОГО ПОРЯДКА.

Назначение этих планов - построение квадратичных регрессионных статических моделей.

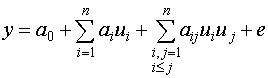
Пусть n=2

Тогда 

Это квадратичная модель, она может быть более адекватна, чем линейная модель.

Планы факторного эксперимента первого порядка неприменимы, так как:

1) они являются двухуровневыми, а через две точки нельзя провести кривую второго порядка;

2) они не позволяют раздельно оценить свободный член модели и коэффициенты при квадратичных переменных.

Существуют специальные планы, которые позволяют строить квадратичные модели регрессии - планы второго порядка.

Существуют три типа таких планов:

1) полный факторный эксперимент (ПФЭ) типа  ;

2) ортогональные центральные композиционные планы (ОЦКП);

3) рототабельные центральные композиционные планы (РЦКП).    

Полный факторный эксперимент типа  .

Это трехуровневый план, спектр которого включает в себя вершины пространства планирования, середины ребер n-мерного гиперкуба и центр пространства планирования. Частоты повторения в всех точках спектра одинаковы.

u1	u2
+1	+1
0	+1
-1	+1
+1	0
0	0
-1	0
+1	-1
0	-1
-1	-1

Основной недостаток такого планирования - чрезмерная избыточность, то есть большое число экспериментов.

Композиционные планы (ОЦКП, РЦКП)

Композиционные планы имеют одинаковую структуру и состоят из трех блоков:

1 блок √ ортогональный план первого порядка (ПФЭ или чаще ДФЭ).

- число точек первого блока.

2 блок - звездные точки, то есть точки, расположенные на координатных осях и удаленные от центра области планирования на величину звездного плеча .

- число звездных точек.

3 блок - центральные точки (точки, расположенные в центре области планирования (ОП)).

- число центральных точек.

- общее число точек плана.

В общем случае такие планы являются пятиуровневыми, так как факторы варьируются на пяти уровнях: - , -1, 0, +1,  .

Поэтому при исследовании реального объекта с неизвестной структурой модели область планирования не должна включать всю область экспериментирования (ОЭ), так как при получении неадекватной линейной модели уточнить структуру в классе квадратичных не удастся из-за невозможности реализации звездных точек.

1 √ ОП

2 √ ОЭ

Необходимо так выбирать интервал варьирования, чтобы выполнялось соотношение: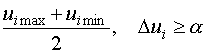 

Отличие ОЦКП и РЦКП заключается в значениях параметров  и  . Для ОЦКП  =1, для РЦКП  >1.    

ОЦКП

Ортогональные центральные композиционные планы (ОЦКП) предназначены для построения квадратичной модели.

Приведем пример ОЦКП.  

n		N			N	3n
2	1,0	4	1	4	9	9
3	1,215	6	1	8	15	27
4	1,414	8	1	16	25	81

n √ число факторов.

1 блок √ ПФЭ.

Чем больше число факторов, тем эффективнее ОЦКП по сравнению с ПФЭ типа 3ⁿ.

При n=2 ОЦКП совпадает с ПФЭ типа 3ⁿ.

Структура ОЦКП

 n=3      

		z0	z1	z2	z3	z4	z5	z6				z7	z8	z9
		u0	u1	u2	u3	u1u2	u1u3	u2u3
		1	+1	+1	+1	+1	+1	+1	1			0.27	0.27	0.27
		1	-1	+1	+1	-1	-1	+1				0.27	0.27	0.27
		1	+1	-1	+1	-1	+1	-1				0.27	0.27	0.27	Первый
		1	-1	-1	+1	+1	-1	-1				0.27	0.27	0.27	блок
		1	+1	+1	-1	+1	-1	-1				0.27	0.27	0.27	ПФЭ
		1	-1	+1	-1	-1	+1	-1				0.27	0.27	0.27
F=		1	+1	-1	-1	-1	-1	+1				0.27	0.27	0.27
		1	-1	-1	-1	+1	+1	+1				0.27	0.27	0.27
		1	1.215	0	0	0			1.2152	0	0	0.75	-0.73	-0.73
		1	-1.215	0	0				1.2152	0	0	0.75	-0.73	-0.73	Второй
		1	0	1.215	0				0	1.2152	0	-0.73	0.75	-0.73	блок
		1	0	-1.215	0				0	1.2152	0	-0.73	0.75	-0.73	ПФЭ
		1	0	0	1.215				0	0	1.2152	-0.73	-0.73	0.75
		1	0	0	-1.215				0	0	1.2152	-0.73	-0.73	0.75
		1	0	0	0				0	0	0	-0.73	-0.73	-0.73	центральная
															точка
			ОЦКП для трех факторов

 

Анализируя полученную матрицу, состоящую из первых десяти столбцов, легко увидеть, что для нее не выполняются все три свойства матриц базисных функций ортогональных планов первого порядка.

Третье свойство выполняется только для первых семи столбцов, т.е. эти столбцы попарно ортогональны.

Второе свойство выполняется лишь в пределах каждой группы столбцов (1-ая группа ╝1 столбец ( ); 2-ая группа ╝2-4 столбцы ( ); 3-я группа ╝ 5-7 столбцы ( ); 4-ая группа ╝ 8-10 столбцы ( ).

Запишем информационную матрицу:

	15	0	0	0	0	0	0	0
	0	8+1.2152
	0
	0
	0
	0
	0
	0							8

Недиагональная часть матрицы появляется за счет того, что последние три столбца неортогональны с другими столбцами и между собой.

Таким образом, полученная матрица не является диагональной, и на ее основе невозможно получить некоррелированные оценки всех неизвестных коэффициентов.

Для обеспечения ортогональности соответствующей ОЦКП матрицы базисных функций необходимо произвести замену квадратичных переменных.

Для нашего плана с=0,73 √ это константа плана. 

Полученная таким образом матрица F является полностью ортогональной. Таким образом, матрица (F^TF), соответствующая преобразованной матрице F, является диагональной. Причем,диагональные элементы одинаковы лишь в пределах каждой группы элементов. Диагональные элементы информационной матрицы уменьшаются при переходе от одной группы коэффициентов к другой. Соответствующие элементы ковариационной матрицы оценок увеличиваются при переходе от одной группы к другой. Таким образом, при реализации ОЦКП оценки неизвестных коэффициентов модели имеют разную дисперсию, то есть находятся с неодинаковой точностью. Точнее всего оценивается свободный член, с меньшей точностью - коэффициенты при линейных членах ( ), еще с меньшей точностью √ коэффициенты при парном взаимодействии ( ). Самые неточные оценки - у коэффициентов при квадратичных членах ( ). В пределах одной группы эти оценки не изменяются. Вычисление МНК-оценок неизвестных параметров.

Определение дисперсий оценок

Оценка i-ого коэффициента определяется следующим образом:

После вычисления МНК оценок необходимо в регрессионную модель подставить выражение для преобразованных квадратов.

Окончательная модель имеет вид:

Дисперсии оценок неизвестных коэффициентов полученной модели определяются следующим образом:

Для этой оценки число степеней свободы =N(m-1), где m-число повторений ОЦКП.    

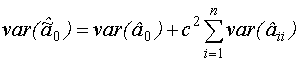
РЦКП

Особенность рототабельных центральных композиционных планов (РЦКП) состоит в том, что: 1) число центральных точек N_{0 >1;} 2) величина звездного плеча  ; 3) вычисление оценок неизвестных параметров производится по более сложным формулам, чем в ОЦКП.

Приведем пример РЦКП  

n			N		N
2	4	1,414	4	5	13
3	8	1,682	6	6	20
4	16	2	8	7	31

Были проведены исследования выражения  , и получены аналитические выражения для МНК-оценок всех групп коэффициентовмодели. Аналитические выражения для оценок неизвестных параметров модели и дисперсий оценок базируются на трех константах, которые вычисляются на основе матрицы РЦКП.

Первая константа  , берутся любые i-й и j-й столбцы

Вторая константа  , берется любой i-й столбец

Третья константа 

Эти константы получаются на основе использования любых двух квадратичных столбцов.

Выражения для дисперсийоценок: