1.2. Составление математической модели оптимизации.

Математическая модель - это образ исследуемого объекта, создаваемый исследователем (субъектом) с помощью определенной формальной (математической) системы с целью изучения (оценки) определенных свойств (или функционирования) данного объекта.

1. Постановка задачи.

Предприятие может выпускать продукцию n типов.

Для производства изделий необходимы m различных видов ресурсов. Известно: нормы затрат ресурсов при выпуске единицы продукции каждого типа, запасы ресурсов в плановом периоде, а также спрос на продукцию. Эффективность возможных вариантов производственной программы предприятия оценивается совокупностью критериев, каждый из которых характеризует некоторую локальную цель. Например, максимизировать выручку от реализации продукции, максимизировать прибыль от реализации продукции и т. д. Требуется определить план производства продукции, оптимизирующий значения всех локальных критериев эффективности.

2.Условные обозначения:

n – количество типов продукции (j = 1,ˉ n),

j - порядковый номер типа продукции (i = 1,ˉm),

m – количество видов ресурсов,

i – порядковый номер вида ресурсов,

– расход i -го ресурса при производстве единицы j -го типа продукции,

b _i – запас i -го ресурса,

α_j, β_j ,– обязательный и максимально возможный объемы производства

j -го типа продукции,

k – количество локальных критериев эффективности,

q – порядковый номер локального критерия эффективности.

x_j – планируемое к выпуску количество j -го типа продукции.

3. Математическая модель задачи.

F¹(x)→ opt,

F²(x) →opt,

F^k (x) →opt,

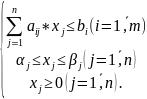
Очевидно, что одновременное достижение целей по всем частным критериям за счёт выбора единого плана производства продукции невозможно. Выход состоит в том, чтобы прибегнуть к некоторому компромиссу в достижении локальных целей.[1]

1.3. Двойственность в линейном программировании

Теория математического линейного программирования позволяет не только получать оптимальные планы с помощью эффективных вычислительных процедур, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, которая является двойственной по отношению к исходной ЗЛП.

Пусть в качестве исходной дана задача:

= c1x1 + c2x2 + ... + cnxn → max;
a11x1 + a12x2 + ... + a1nxn ≤ b1, a21x1 + a22x2 + ... + a2nxn ≤ b2, ...             am1x1 + am2x2 + ... + amnxn ≤ bm;	(1)
xj ≥ 0,

Задача линейного программирования, двойственная задаче (1), будет иметь вид:

= b1y1 + b2y2 + ... + bmym → min;
a11y1 + a21y2 + ... + am1ym ≥ c1, a12y1 + a22y2 + ... + am2ym ≥ c2, ...             a1ny1 + a2ny2 + ... + amnym ≥ cn;	(2)
yi ≥ 0,   .

Можно сформулировать правила построения двойственной задачи из задачи исходной.

1. Если в исходной задаче ищется максимум целевой функции, то в двойственной ей - минимум.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи.

3. В исходной ЗЛП все функциональные ограничения - неравенства вида “≤”, а в задаче, двойственной ей, - неравенства вида “≥”.

4. Коэффициенты при переменных в системах ограничений взаимно двойственных задач описываются матрицами, транспонированными относительно друг друга.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой.

6. Условие неотрицательности переменных сохраняется в обеих задачах.

Связь между оптимальными планами взаимно двойственных задач устанавливают теоремы двойственности.

Теорема 1. Если одна из двойственных задач имеет конечный оптимум, то другая также имеет конечный оптимум, причем экстремальные значения целевых функций совпадают:

.

(3)

Если целевая функция одной из двойственных задач не ограничена, то условия другой задачи противоречивы.

Теорема 2 (о дополняющей нежесткости). Для того чтобы план и план являлись оптимальными решениями, соответственно, задач (2) и (3) необходимо и достаточно, чтобы выполнялись следующие соотношения:

	(4)

Таким образом, если компонент оптимального плана больше нуля, то при подстановке в соответствующее ограничение двойственной задачи оптимального плана это ограничение обращается в верное равенство, и наоборот.

Теорема об оценках. Значения переменных в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i в системе ограничений прямой задачи на величину целевой функции :

(5)

Компоненты оптимального решения двойственной задачи принято называть двойственными оценками. Часто употребляется также термин «объективно обусловленные оценки».

На свойствах двойственных оценок базируется экономико-математический анализ распределения ресурсов. В пределах устойчивости двойственных оценок имеют место свойства, рассмотренные ниже.

Перейдем к рассмотрению свойств двойственных оценок.

Свойство 1. Оценки как мера дефицитности ресурсов. Двойственные оценки отражают сравнительную дефицитность факторов производства. Чем выше величина оценки , тем выше дефицитность i-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство.

Свойство 2. Оценки как мера влияния ограничений на значение целевой функции. Величина двойственной оценки какого-либо ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на единицу. В связи с этим значение объективно обусловленной оценки иногда называют теневой ценой ресурса. Теневая цена - это стоимость единицы ресурса в оптимальном решении.

Однако нужно учитывать, что двойственные оценки позволяют измерить эффективность лишь незначительного изменения объема ресурсов. При значительных изменениях может быть получен новый оптимальный план и новые двойственные оценки.

Свойство 3. Оценки как инструмент определения эффективности отдельных хозяйственных решений. С помощью двойственных оценок можно определить выгодность выпуска новых изделий, эффективность новых технологических способов производства. При этом эффективным может считаться тот вариант производства, для которого сумма прибыли, недополученной из-за отвлечения дефицитных ресурсов, будет меньше прибыли получаемой. Разница между этими величинами (Δ_j) вычисляется как:

(6)

В том случае, если Δ_j ≤ 0, вариант производства является выгодным, если Δ_j > 0 – вариант невыгоден.

Свойство 4. Оценки как мера относительной заменяемости ресурсов с точки зрения конечного эффекта. Например, отношение / показывает, сколько единиц k-го ресурса может быть высвобождено при увеличении объема i-го ресурса на единицу, для того чтобы максимум целевой функции остался на прежнем уровне; или наоборот, сколько единиц k-го ресурса необходимо дополнительно ввести при уменьшении на единицу объема i-го ресурса, если мы хотим, чтобы значение целевой функции не изменилось.

Завершая рассмотрение вопроса, отметим, что применение теорем двойственности позволяет, зная оптимальное решение одной из взаимно двойственных задач, без труда отыскать оптимальное решение другой задачи. [3]