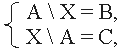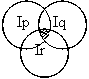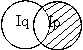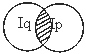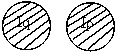Часть I. Тест Множества и операции над ними

№ п/п

Вопрос

Варианты ответов:

1

Укажите верное утверждение для всех A, B и C:

   Если A B и B C, то A C    Если A B и B C, то A C    Если A B C и A C B, то A C = ;

2

Решить систему уравнений

где A, B и C – данные множества и B A C.

  X = ( C \ A ) B.   X=C B.   X=(C A) B.

3

Решить систему уравнений

где A, B и C – данные множества и B A,

A C = .

   X = ( A \ B ) C.    X= ( A C) B.

4

Существуют ли такие множества A, B и C, что A B , A C = , (A B) \ C = ;

  нет;    да.

5

Образуют ли бинарные отношения группу относительно операций

  нет;    да

№ п/п

Вопрос

Варианты ответов:

1

Какие из следующих предложений не являются высказываниями?

   Треугольник ABC подобен треугольнику A`B`C`.    Студент физико-математического факультета педагогического института.    Москва – столица СССР.

2

Установите, какие из высказываний в следующих парах являются отрицаниями друг друга:

   2=<0, 2>0;    6<9, 6>9;    Функция f – четна, функция f – нечетна;    Треугольник ABC прямоугольный, а ABC – тупоугольный;

3

Пусть высказывание A B истинно. Что можно сказать о логическом значении высказывания ( A B ) ( A B ) ?

   Истинно;    Ложно.

4

Существует ли три таких высказывания A, B и C, чтобы одновременно высказывание A B было истинным, высказывание A C и высказывание (A B) C – ложным?

   Не существует;    Существует.

5

Применяя равносильные преобразования, приведите следующие формулы к возможно более простой форме:

( P Q ) ((P Q ) P) ;

   P Q;    1;    P.

6

Следующую формулу преобразуйте равносильным образом так, чтобы она содержала только операции и :

( x y ) ( x z )

   ( x y z );   x y.

7

Определите, какая из последовательностей символов является формулой:

  ((P Q) R) S;   ((P ( Q R )) (( P R ) Q )).

8

Приведите к ДНФ:

(x y) ( z T )

   (x y z T) ( x y z T);    x y z.

9

Приведите к КНФ:

( x z ) (x y);

   x z;    x z .

10

 По данному набору значений переменных постройте дизъюнктивный одночлен, принимающий значение только на этом наборе значений переменных:

( , )

   x y;    x y;   x y z.

№ п/п

Вопрос

Варианты ответов:

1

Укажите, видом какой формы и из каких посылок является следующая формула :

A C, (A C) ((D C) (A B C)), (B C) (A B C), B C, A B C, A B, C

   A C, B C, A B.    A C, B C, A B C.

2

Какие из следующих выражений являющиеся формулами исчисления высказываний :

   ((p1 p2) (p1 p2)) ;    (p1 (p2 p3)) p3;

3

Доказать, что: H = {A} B A

   B A;    A, A (B A), B A;    B A C.

4

Доказать, что: H = {A C}

   A C,(A C) ( ), ;    ( C).

5

Дана формула A = x1 x2 x3 и набор значений переменных (0,0,1). Записать вывод формулы A или ее отрицание из соответствующей совокупности формул:

  , , x3, x3 (x1 x2 x3), x1 x3 x3;    x2;

6

Пусть A = x1 & x3 и набор значений переменных (1, 0, 1). Тогда {x1, ,x3} A.

Записать вывод.

  x1 & x2 x3;   H x1, , x3, x3 (x1 & x3), x1 & x3 A.

№ п/п

Вопрос

Варианты ответов:

1

Указать область истинности предиката: X+5=1.

   Ip={-2};    Ip={-4};    Ip={4};

2

Указать область истинности предиката: X²-2X+1=0.

  Ip={1};   Ip={2};

3

Выяснить, какие из следующих предикатов являются тождественно истинными:

   X²+Y²>=0;    X²+Y²>0;    X²+1>=(X+1)².

4

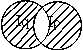
Записать предикат, полученный в результате логических операций над предикатами P(x), Q(x) и R(x) , область истинности которого I заштрихована на рисунке

   P(x) & R(x);    P(x) & Q(x) & R(x).

5

Даны предикаты P(x): X²+X+1>0 и Q(x) : X²-4X +3=0, определенные на множестве R. Установите , какие из следующих высказываний истинны:

 x P(x); y P(x).

6

Укажите, какие из следующих выражений являются формулами логики предикатов:

  x y P(x,y);   x,y P(x,y).

7

Пусть A(x) и B(x)- любые предикаты. Какие из следующих формул равносильны формуле: A(x)

A(x) B(x); ; B(x); A(x); & B(x).

8

Записать предикат, полученный в результате логических операций над предикатами P(x) , Q(x) и R(x) , область истинности которых (I) заштрихована на следующем рисунке:

P(x) & ; P(x) & Q(x).

9

Записать предикат, полученный в результате логических операций над предикатами P(x) ,Q(x) и R(x) , область истинности которых (I) заштрихована на следующем рисунке:

P(x) & R(x); P(x) & Q(x).

10

 Записать предикат, полученный в результате логических операций над предикатами P(x) ,Q(x) и R(x) , область истинности которых (I) заштрихована на следующем рисунке:

P(x) & ; P(x) & & Q(x).

11

 Записать предикат, полученный в результате логических операций над предикатами P(x) ,Q(x) и R(x) , область истинности которых (I) заштрихована на следующем рисунке:

  P(x) Q(x);   P(x) Q(x);    .