3.3. Изгибаемые элементы

На изгиб в строительных конструкциях работают, как правило, балки, прогоны, доски настилов и другие подобные им элементы, которые испытывают действие нагрузок равномерно распределенных по всему пролету, либо приложенные сосредоточенные в одной или нескольких точках. Величина внутренних усилий от любых нагрузок вычисляется по правилам строительной механики.

Рис. 6. Характер распределения нормальных (А) и касательных (Б) напряжений в изгибаемом элементе

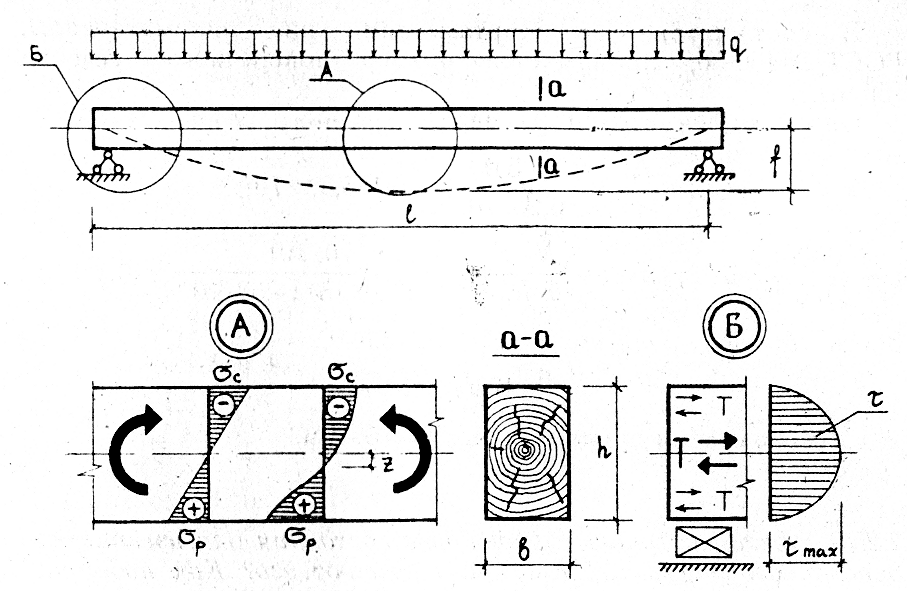
Изгибаемые элементы рассчитывают по первому и второму предельным состояниям (на прочность и жесткость). В расчете по первому предельному состоянию используют расчетную нагрузку, а при определении прогиба нормативную нагрузку, т.е. без учета коэф - та перегрузки.

Расчет деревянных элементов на изгиб по нормальным напряжениям производят приближенно. При более точном методе потребовался бы учет различных значений модулей упругости в сжатой и растянутой зонах (рис. 7).

Рис. 7. Относительная приведенная диаграмма работы древесины при растяжении и сжатии (напряжения в долях от R_пч, а деформации в %)

1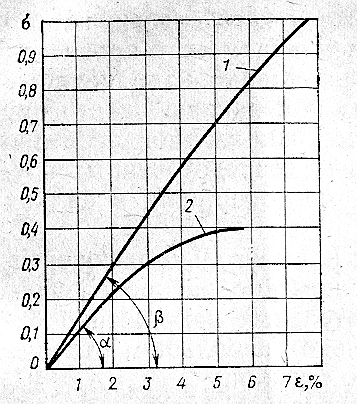 – при растяжении (модуль упругости = tgβ);

2 – при сжатии (модуль упругости = tgα)

Из этого графика видно, что в сжатой зоне развиваются большие пластические деформации, которые нарушают прямолинейность распределения нормальных напряжений по высоте сечения. Поэтому, нормальные напряжения определяют при двух допущениях:

1. Считают, что модули упругости в растянутой и сжатой зонах равны, т.е. Е_с=Е_р;

2. И принимается прямолинейное распределение напряжений по высоте элемента (рис. 7).

Р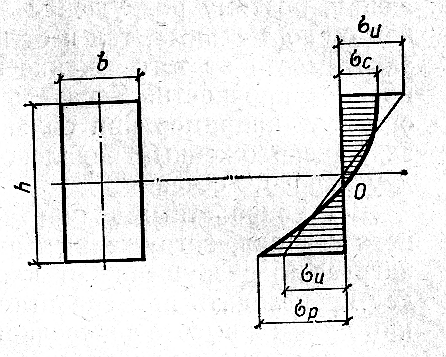 ис. 8. Распределение нормальных напряжений по высоте поперечного сечения при поперечном изгибе балки

При этих допущениях нормальные напряжения в элементах, которые обеспечены от потери устойчивости плоской формы деформирования определяются по условию:

• 1) расчет на прочность по нормальным сечениям

σ_и = М/W_нтm_б ≤ R_и; (15)

При определении W_нт ослабления сечений, расположенные на участке длиной 200мм, совмещаются в одно сечение; m_б – коэффициент, который учитывает размеры сечения.

Прочность проверяют в сечении, где действуют наибольшие изгибные напряжения, и в сечениях, где имеются ослабления. Если максимальный момент находится за зоной с ослаблениями, то расчет производится дважды:

• на М_max;

• на М в зоне с ослаблениями.

R_и – расчетное сопротивление древесины при изгибе. R_и= R_с.

• 2) Расчет на скалывание при изгибе

τ=Q_max·S_бр/I_бр·b_расч ≤ R_ск (16)

S=bh²/8; J=bh²/12;

S_бр – статический момент сдвигаемой части сечения;

J_бр – момент инерции поперечного сечения элемента;

b_расч – ширина (фактическая) элемента, учитываемая в расчете;

b_расч=0,6b (для клееных элементов) – коэффициент непроклеивания.

• на устойчивость плоской формы изгиба

Помимо расчета на прочность изгибные элементы (особенно при их малой ширине) проверяют также на устойчивость плоской формы деформирования при изгибе.

σ = М_max/φ_м·W_бр ≤ R_и (17)

φ_м – коэффициент устойчивости плоской формы изгибаемых элементов, который определяется по формуле:

φ_м=140(b²/l_расч·h)·k_ф.

l_расч – расстояние между опорными сечениями элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба – расстояние между этими точками;

М_max, W_бр, φ_м определяются на участке l_расч.

k_ф – коэф-нт, учитывающий форму эпюры изгибающих моментов (определяется по СНиП);

При расчете одно и 2-х скатных балок значение коэффициента φ_м дополнительно умножается на k_ж.м (по СНиП). При наличии раскреплений по растянутой кромке на участке l_расч – k_ж.м.

Для клеефанерных элементов коробчатого и двутаврового сечений расчет на устойчивость производится из условия:

σ=M_max/φW_прив≤R_с

где W_прив – момент сопротивления приведенного сечения (приводят к материалу древесины);

φ – коэффициент продольного изгиба, определяется на участке l_расч для сжатого пояса из его плоскости.

В виду повышенной жесткости клеефанерные панели СНиП допускает не рассчитывать на устойчивость.

• По II группе предельных состояний. По деформациям:

f= f_о / k (18)

где f_о – прогиб балки постоянного сечения без учета сдвиговых деформаций; k – нормативный коэффициент, который учитывает деформации сдвига от поперечной силы.