4.2. Целостность технологического потока

Решение проблемы развития технологических линий связано с расчетом уровня целостности существующих технологических систем через экспериментальное определение стабильности отдельных подсистем. Понятие стабильности более широкое, чем устойчивости. Стабильный процесс – это процесс, утвердившийся на определенном уровне устойчивости. И если устойчивость характеризует качество функционирования системы, то стабильность – уровень организованности, целостности системы, уровень ее развития.

Одной из характеристик систем является энтропийная функция:

(4.1)

где – мера множества состояний системы (i = 1, 2, …).

В большинстве случаев понятия энтропийной функции и энтропии оказываются тождественными, т. е. в качестве μ_i задается вероятностная мера, обозначаемая обычно в виде множества (P_i, i = 1, 2, ...).

Использование энтропии:

(4.2)

где

Состояние системы, соответствующее максимуму энтропийной функции Н_max, можно представить как «бесструктурное» множество элементов данной совокупности. Поэтому мера организованности системы равна разности максимально возможной энтропии системы и энтропии данного множества элементов, имеющих определенную структуру, т. е.

∆H = H_max – H. (4.3)

Пронормировав H путем деления на Hmax, получим:

 = 1 – Н / Н_max, (4.4)

где η – стабильность процесса;

H – энтропия, соответствующая данному распределению значений величины показателя качества промежуточного продукта или изделия;

H_max – максимально возможная энтропия, соответствующая закону равномерного распределения.

Количественно энтропия определяется по формуле

(4.5)

Для случая с двумя врозможными результатами формула (4.5) примет вид:

(4.6)

Функция (4.6) показывает, что энтропия меняется от нуля до определенного максимального значения, причем значение «0» имеет место тогда, когда Р = 0 и Р = 1, т. е. когда распределение практически отсутствует и неопределенности в системе нет. Максимального значения энтропия достигает при равной вероятности отдельных наблюдений (Р = 0,5), и, следовательно, распределение обладает полной неопределенностью.

H_max = –0,5 log₂ 0,5 – 0,5 log₂ 0,5 = 1 бит.

Для подсчета энтропии процесса необходимо у каждой подсистемы экспертным путем выделить один или несколько контролируемых параметров, существенно влияющих на функционирование следующей подсистемы и всю технологию в целом. В тех подсистемах, где несколько контролируемых параметров, экспертным путем устанавливают коэффициент весомости т каждого параметра, причем m₁ + m₂ + ... + т_п = 1.

Из технологических инструкций, стандартов и других источников устанавливают базовые и допустимые значения параметров, при которых продукт соответствует требованиям стандарта. Затем вычисляют стандартное значение комплексного показателя К_СТ:

К_СТ = m₁Б₁ / Д₁ = m₂Б₂ / Д₂ + … + m_nБ_n / Д_n,

где Б₁, Б₂, …, Б_n – базовые значения параметров (лучшие значения параметров из предусмотренных стандартами, ТУ, ТИ);

Д₁, Д₂, ..., Д_n – допустимые значения тех же параметров.

При этом, если численное выражение базового значения параметра превышает численное выражение допустимого (или фактического) значения, то в числитель подставляют меньшее, а в знаменатель – большее значение.

Интервал колебаний показателя К_СТ находится в пределах от 0 до 1.

Диагностика проводится в течение определенного отрезка времени с фиксацией значений параметров за определенный интервал при установившемся режиме работы оборудования.

Если при этом у подсистемы выделен лишь один контролируемый параметр, то анализ совокупности экспериментальных данных осуществляют следующим образом.

Все образцы выборки (n) раскладывают на две группы: образцы, входящие в пределы допуска на параметр процесса (n₁), и образцы, не входящие в пределы допуска на параметр процесса (n₂), причем n = n₁ + n₂.

В тех подсистемах, где несколько контролируемых параметров, для каждого замера сначала вычисляют фактическое значение комплексного показателя:

K_ф = m₁F₁ / Д₁ = m₂F₂ / Д₂ + … + m_nF_n / Д_n,

где F₁, F₂, ..., F_n – фактические значения параметров.

Затем все образцы выборки (n) также раскладывают на две группы: образцы, показатель К_ф которых колеблется в пределах К_СТ до 1 (n₁), и образцы, показатель К_ф которых находится в пределах от 0 до К_СТ(n₂).

Далее осуществляется подсчет вероятности Р(х) попадания показателя К_ф в соответствующий интервал:

P = n₁ / n и (1 – Р) = n₂ / n

Энтропию подсчитывают по формуле (4.6).

При этом величина интервала должна быть, по крайней мере, в два раза выше точности измерения исследуемой величины.

Несоблюдение этого условия может привести к тому, что некоторая доля образцов, отнесенная к одному интервалу, на самом деле должна быть отнесена к другому.

Понятие стабильности процесса может быть использовано при исследовании качественной и количественной изменчивости продукта, получаемого в результате данного процесса. При исследовании качественной изменчивости задача упрощается, так как известна граница двух интервалов, на которые можно разбить всю совокупность образцов: удовлетворяющие требованиям стандарта и не удовлетворяющие им. Исследование же количественной изменчивости продукции требует установления границ интервалов, если они не оговорены в нормативно-технической документации.

Таким образом, стабильность подсистемы технологической системы оценивается показателем, который для бинарной подсистемы (т. е. подсистемы с двумя возможными состояниями процесса по параметру, являющемуся значимым для состояния последующей подсистемы), будет:

η_i = 1 – Н_i / Н_{i max}, (4.7)

где η_i и Н_i – стабильность и энтропия i-й подсистемы.

Рассмотрим в качестве технологической системы совокупность трех подсистем С, В и А. Подсистема С может иметь п состояний (С₁, С₂, ..., С_п) с вероятностями P_(C1), P_(C2), …, P_(Cn). Соответственно, подсистема В имеет т состояний (В₁, В₂, ..., В_m) с вероятностями P_(B1), P_(B2), …, P_(Bm), а подсистема А-r состояний (А₁, А₂, ..., А_r) с вероятностями P(A₁), Р(А₂), …, Р(А_r). Состояние технологической системы находится в одном из следующих C_nB_mA_r возможных состояний.

Для вычисления энтропии системы СВА достаточно составить сумму произведений вероятностей состояний подсистемы на их логарифмы:

(4.8)

Когда подсистемы С, В и А статистически независимы, т. е. реализация одного из состояний любой подсистемы не влияет на вероятность возможного состояния других подсистем,

(4.9)

Энтропия системы в соответствии с равенствами (4.8), (4.9):

(4.10)

а уровень целостности системы, принимая во внимание уравнение (4.7), может быть определен таким образом:

(4.11)

Когда подсистемы С, В и А статистически зависимы,

Р_(СВА) = Р_(С)Р_(В/С)Р_(А/СВ), (4.12)

где величины Р_(В/С) и Р_(А/СВ) – условные вероятности событий в подсистемах А и В.

Из соотношений (1.9) и (1.10) следует, что энтропию технологической системы как совокупности статистически зависимых подсистем можно записать так:

Н_(СВА) = Н_(С) + Н_(В/С) + Н_(А/СВ). (4.13)

Первое слагаемое правой части этого выражения представляет собой энтропию подсистемы С. Что касается второго, то это есть среднее значение энтропии подсистемы В при различных возможных реализациях состояний подсистемы С; третье слагаемое – среднее значение энтропии подсистемы А при различных реализациях состояний подсистемы С и В. Таким образом, Н_(В/С) – условная энтропия подсистемы В относительно подсистемы С, а Н_(А/СВ) – условная энтропия подсистемы А относительно подсистем С и В.

Условная энтропия характеризует статистическую связь между подсистемами. Если такая связь отсутствует, т. е. Р_(В/С) = Р_(В), получаем Н_(В/С) = Н_(В) (условная энтропия подсистемы совпадает с ее безусловной энтропией). При наличии детерминированной связи состояний подсистем С и В условная вероятность имеет два значения: P_(В/С) = 1 или Р_(В/С) = 0. Так как для обоих значений Р_(В/С)logР_(B/C) = 0, то для системы с детерминированной связью H_(В/С) = 0. В общем случае условная энтропия лежит в пределах 0 ≤ Н_(В/С) < Н_(В).

Уровень целостности системы из трех статистически зависимых подсистем с учетом соотношений (4.7) рассчитывают по формуле

(4.14)

где η_В/С – условная стабильность подсистемы В относительно подсистемы С; η_А/СВ – условная стабильность подсистемы А относительно подсистемы С и В.

Вид формулы для расчета уровня целостности системы зависит от числа подсистем в системе и ее структуры. Правая часть формулы содержит такое число отрицательных единиц, которое на одну меньше количества подсистем в системе.

Стабильность каждой системы устанавливают экспериментально за определенный период. Комплекс методик в этом всестороннем обследовании системы по аналогии с медицинским назван диагностикой.

Понятия системности, организованности и самодвижения, развиваемые ныне на уровнях познания действительности, означают, что явления развития в целом можно рассматривать как борьбу двух противоположных тенденций – организации и дезорганизации. При этом процесс развития начинающейся энтропии может быть описан в общем как процесс накопления структурной информации, исчисляемой как разность между максимальным и реальным значениями энтропии, т. е. ростом стабильности.

Следовательно, явления развития целесообразно рассматривать в координатах, связанных с понятиями стабильности и структуры системы, с возможностью отсчета уровня организации (целостности) системы на всех этапах ее развития.

Таким образом, модель развития объекта получает трехмерное пространство (на рис. 4.1 показан продольный разрез процесса развития), в котором энтропия убывает от периферии к центру, а стабильность растет от периферии к центру (ось ). На другой оси показан рост структуры (усложнения) объекта с ростом количества его подсистем, элементов (ось L). Здесь – средняя стабильность подсистем в системе, L – количество подсистем в системе.

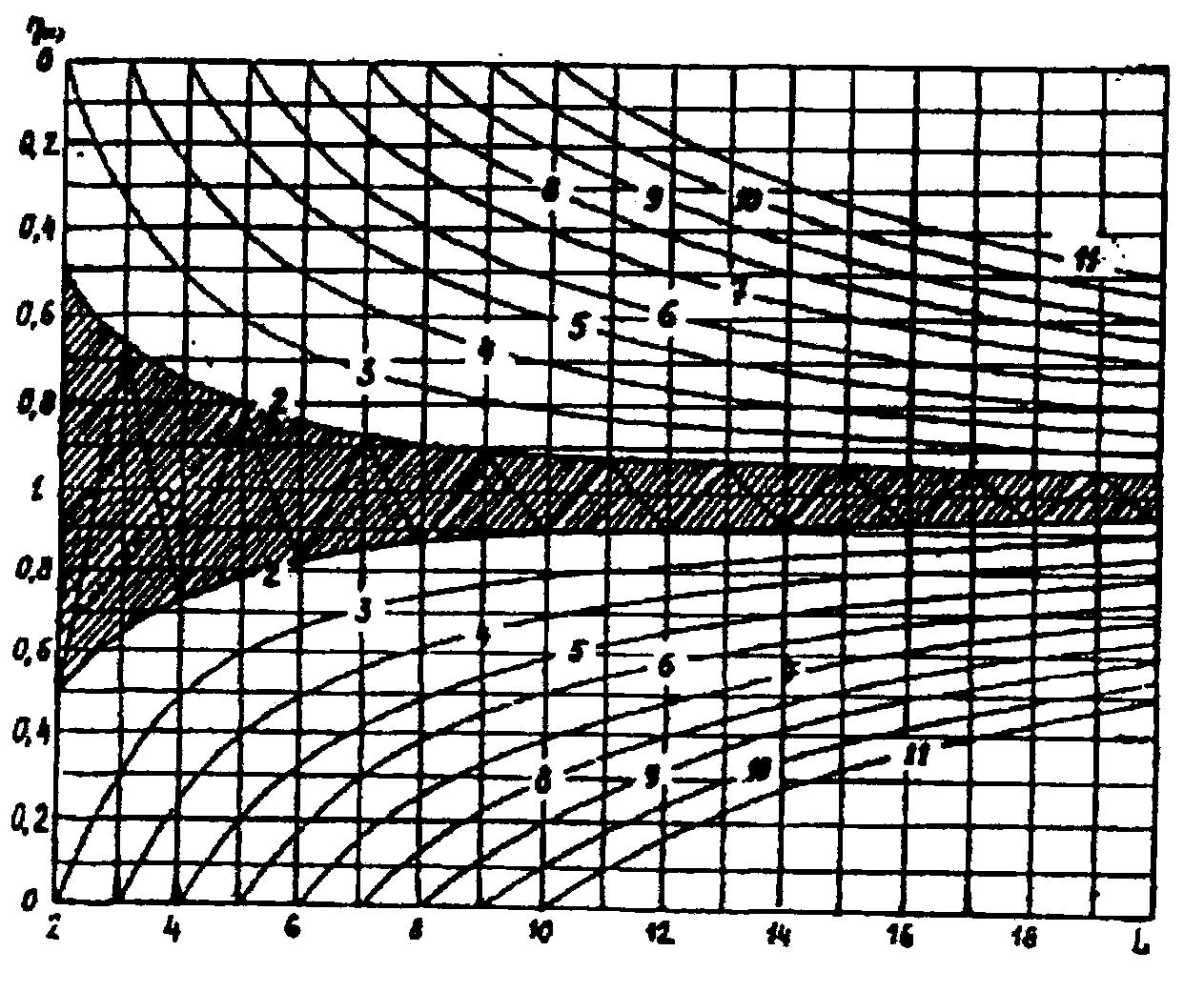
Рис. 4.1. Модель процесса развития технологической системы

(спираль развития) при различных уровнях ее организации

(целостности): (+1,0); 2 – (0,0); 3 – (–1,0); 4 – (–2,0); 5 – (–3,0); 6 – (–4,0);

(–5,0); 8 – (–6,0); 9 – (–7,0); 10 – (–8,0); 11 – (–9,0)

В совокупности это означает возрастание уровня организации данного объекта в процессе его развития. Причем если развитие идет вследствие усложнения технологии, необходимо повысить стабильность функционирования всех ее частей. Если же развитие идет в результате упрощения технологии, то можно уменьшить стабильность функционирования ее составляющих.

Рассмотрим подробно рис. 4.2. По оси ординат от точки 1 вверх и вниз отложена уменьшающаяся до 0 стабильность функционирования подсистем системы. По оси абсцисс – количество подсистем в системе от 2 до 20. Сходящиеся кривые – уровни целостности системы, которые при уровне целостности Θ = +1 вырождаются в прямую, параллельную оси абсцисс. Заштрихованную область можно назвать областью целостных систем: их целостность находится в диапазоне от Θ = 0 до Θ = 1. Остальное поле графика – область плохо организованных, суммативных систем. Целостность этих систем уменьшается от Θ = 0 до Θ = –9. Сами эти кривые есть огибающие сходящихся спиралей развития, размещенных между двумя кривыми одного уровня целостности.

Как стабильности подсистем, так и целостности системы, измеряются в относительных единицах (бит/бит). Если стабильность каждой из подсистем равна единице (максимальное значение), то уровень целостности всей системы также равен единице. Если стабильность каждой из подсистем равна 0 (минимальное значение), то уровень целостности всей системы равен такому количеству отрицательных единиц, которое на одну меньше числа подсистем в системе. В первом крайнем случае мы имеем дело с идеально организованной целостной системой, а во втором крайнем случае система представляет собой разобщенные, произвольно функционирующие составные части, совокупность которых образует простую суммативную систему.

Следует подчеркнуть, что значение уровня целостности во многом зависит от отрезка времени, за который производится его оценка, и поля допуска на выход подсистем. Чем меньше отрезок времени и шире поле допуска, тем при прочих равных условиях значение уровня целостности системы будет выше.

Таким образом, сходящаяся спираль отображает целенаправленность процессов развития, конкретизируя их как движение к неэнтропийной устойчивости, к определенной детерминации.

В процессе развития технологических систем повышается их уровень целостности, проявляющийся в функциональном и структурном отношениях. Функциональная целостность системы рассматривается в ее отношении к внешней среде, структурная – в отношении к ее составным частям.

Повышение функциональной целостности технологических систем выражается в расширении функциональных возможностей системы, соответствующих требованиям внешней среды при минимальных усложнениях ее структурной организации.

Повышение структурной целостности достигается уменьшением числа элементов и упрощением связей между ними. Повышению структурной целостности способствует сокращение числа физических принципов, используемых для создания системы.

Из рис. 4.2, фрагмента общей модели процесса, следует, что развитие технологической линии как системы процессов, т. е. переход с низшего уровня целостности к высшему, возможен как при сокращении числа подсистем в системе (путь 1 – совершенствование структуры), так и при модернизации процессов в подсистемах (путь 2 – совершенствование элементов). Работы по автоматизации поточной линии (путь 3 – совершенствование связей) имеют смысл, если совокупность процессов в машинах и аппаратах представляет собой целостную систему (Θ > 0). Поэтому величина уровня целостности может служить и показателем готовности линии к приему средств автоматизации. Путь 4 есть комбинация вышеперечисленных направлений развития системы.

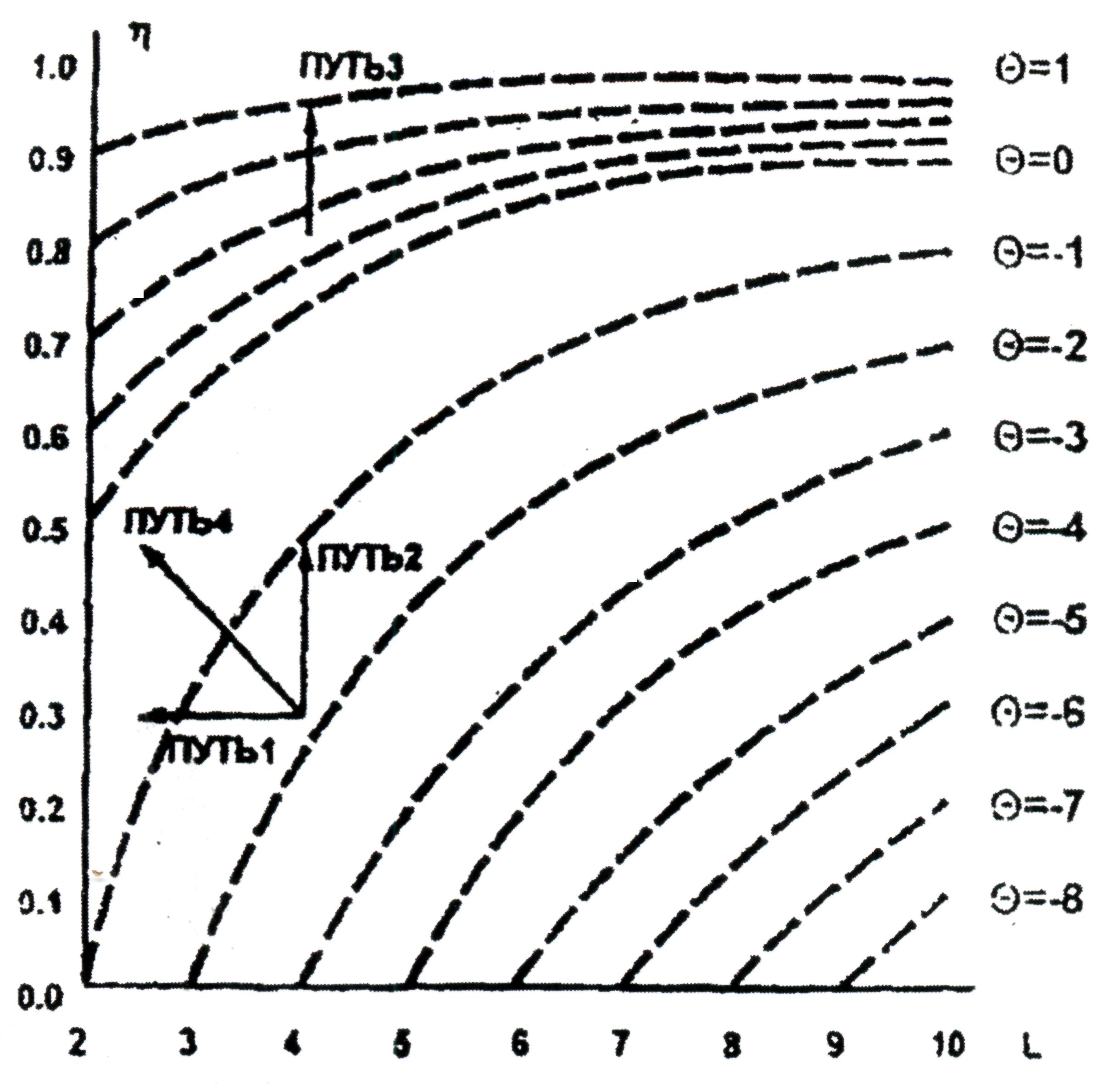
Рис. 4.2. Зависимость целостности систем Θ от средней

стабильности подсистем η и их количества L

Любую операцию можно охарактеризовать как совокупность параметров, находящихся на определенных уровнях развития. Параметры в процессе эволюции развиваются от неконтролируемых через контролируемые, регулируемые путем поддержания значений параметров на заданном уровне к управляемым и саморегулируемым. Для оценки уровня развития условно принимается пятибалльная шкала.

Специалист-эксперт в состоянии выделить среди бесчисленного множества параметров значимо влияющие на процесс.

Любой процесс, следовательно, в принципе можно охарактеризовать совокупностью параметров, находящихся на разных уровнях развития.

Количественную оценку уровня развития технологического процесса (У_Т), описываемого комбинацией параметров, находящихся на различных уровнях, можно представить в виде средневзвешенной величины параметров:

(4.16)

где п – число параметров, значимо влияющих на процесс; F_i – число параметров, находящихся на i-уровне развития параметра; К_i – балльная оценка i-уровня развития параметра.