В.4. Основные требования, предъявляемые к сау

Кроме общетехнических требований (масса, габариты, цена, и т.д.) каждая АС должна удовлетворять следующим основным специальным техническим требованиям:

обеспечивать в любых условиях требуемое количество управления на установившихся и переходных режимах в различных условиях эксплуатации в течение гарантированного времени;

обеспечивать хорошую управляемость объекта. Во всем диапазоне перемещения ручки управления должно обеспечиваться непрерывное изменение управляемого параметра за исключением специально предусмотренных участков. Допускается предусмотренное конструктором скачкообразное изменение управляемого параметра при срабатывании элементов механизации объекта управления;

не ограничивать скорость перемещения ручки управления на всех режимах во всех условиях эксплуатации. При этом переходные процессы в объекте управления должны осуществляться без его перегрева и нарушения устойчивой работы;

не требовать дополнительных регулировок в эксплуатации при различных атмосферных условиях и температурах одного и того же сорта рабочего тела;

иметь в случае электронной автоматической системы, блоки встроенного контроля с целью исключения аварийных режимов работы объекта управления при отказах АС и перехода на резервную систему и т.д.

По мере развития и усложнения техники и автоматических систем все большее значение приобретают эргономические требования к ним. Основная задача эргономики - это решение задачи оптимального распределения функций управления между человеком и автоматикой. Определяющим для автоматических систем силовых установок является требование максимального упрощения действий оператора при задании режима работы двигателя. Кроме того, должна быть обеспечена:

возможность эффективного контроля за работой АС;

возможность своевременного и эффективного вмешательства оператора в работу АС с целью парирования отказов.

Удовлетворение вышеперечисленных требований достигается следующими путями:

использованием новейших достижений науки, техники и технологии производства;

всесторонним изучением и глубоким анализом отечественного и зарубежного опыта создания и эксплуатации технических устройств;

предусмотрением возможностей последующего развития и улучшения характеристик АС;

учетом при разработке АС требований надежности, живучести, контролепригодности, производственной, эксплуатационной и ремонтной технологичности;

применением новых методов конструирования;

многоцелевым использованием основных элементов конструкции агрегатов АС;

широким применением стандартных и унифицированных элементов конструкции агрегатов АС.

В.5. Проблемы современной теории автоматического управления

Теория автоматического управления (ТАУ) является теоретической основой, на базе которой разрабатываются большинство автоматических устройств. Предметом изучения ТАУ являются принципы построения, методы анализа и синтеза широко распространенных систем автоматического регулирования и управления.

Основоположником ТАУ, зародившейся немногим более века назад, является проф. Петербургского технологического института И.А. Вышнеградский (1831—1895). Основы ТАУ были изложены в его работе "О регуляторах прямого действия" (1876 г.) Он впервые показал, что процессы в устройстве управления и связанном с ним объектом неразрывно связаны между собой и требуют совместного исследования.

В устройствах управления важное место занимает проблема обеспечения устойчивости движения. Основоположником строгой теории устойчивости является профессор Харьковского университета А.М. Ляпунов (1857-1918).

Мир технических систем разнообразен. Однако математика и физика выявили простые параллели в этом сложном мире. Система параллелей позволяет понять, что математическое описание процессов движения координат систем принадлежащих разным энергетическим доменам подобно, и может быть предметом изучения одной науки, которая называется "Теория систем автоматического регулирования". Более того, в последние годы, приобретен успешный опыт применения методов этой теории при решении задач управления в экономических, финансовых и других нетехнических системах.

В теории автоматического регулирования основными являются проблемы: устойчивости, качества переходных процессов, статической и динамической точности, автоколебаний, оптимизации, синтеза и отождествления (идентификации).

В.1. Классификация автоматических систем.

По назначению, характеру управляемых величин,

по виду используемой энергии

По назначению можно отличать системы управления ЛА, системы управления ТРД, системы управления бортовым оружием и т. д.

По характеру управляемых величин можно различать системы управления курсом самолета, системы управления частотой вращения ротора ТРД и т. д.

По виду используемой энергии системы можно разделить на электрические, гидравлические, пневматические и т. д.

По принципам построения

САУ подразделяются на системы работающие на:

• принципе отклонения ;

• принципе компенсации возмущений;

• комбинированные;

• адаптивные.

По характеру изменения заданного значения

управляемой величины по времени

САУ, построенные на принципе отклонения, разделяются на три класса: системы стабилизации, программные системы и следящие системы.

а) система стабилизации поддерживает с заданной точностью постоянное значение управляемой величины.

б) программная система обеспечивает изменение управляемой величины по заранее составленной программе, являющейся функцией времени.

в) следящая система изменяет управляемую величину в соответствии с заранее неизвестной функцией времени, которая может создаваться либо с помощью задающего ручного воздействия, либо дополнительным устройством.

В следящей системе управляемая величина должна следить за задающим воздействием, являющимся неизвестной функцией времени.

По наличию ошибок на установившемся (статическом) режиме

По точности управления при воздействиях, удовлетворяющих определенным условиям, системы подразделяются на астатические и статические.

Система, которая обеспечивает нулевую ошибку управляемой величины, при стремлении с течением времени конкретного воздействия к некоторому постоянному значению, называется астатической по отношению к этому воздействию.

Система называется статической если при воздействии, стремящемся с течением времени к постоянной величине, ошибка управляемой величины также стремиться к постоянному значению, зависящему от уровня воздействия.

Понятие статической и астатической систем может относиться и к задающему и к возмущающему воздействиям.

Одна и та же САУ может быть статической к какому либо возмущающему воздействию и астатической по отношению к задающему воздействию и наоборот.

По характеру передачи и преобразования сигналов

САУ подразделяются на непрерывные и дискретные. В непрерывных системах сигналы передаются и обрабатываются каждое мгновение, т. е. сигналы являются непрерывными функциями времени. В дискретных системах сигналы поступают не постоянно, а прерывисто.

В зависимости от идеализации, принятой при математическом описании

САУ подразделяются на линейные и нелинейные. Линейные САУ описываются линейными уравнениями, или операторами. Их математическая модель линейна. Нелинейные системы имеют нелинейную математическую модель.

В.2 .Принципы построения автоматических систем

Несмотря на большое разнообразие объектов управления, а также задач и целей, обеспечиваемых автоматическими управляющими устройствами, число принципов построения САУ невелико.

Различают четыре принципа построения САУ:

• по отклонению управляемой величины;

• по возмущающему воздействию;

• комбинированный (по отклонению и возмущающему воздействию);

• адаптации (приспособления)

По отклонению управляемой величины

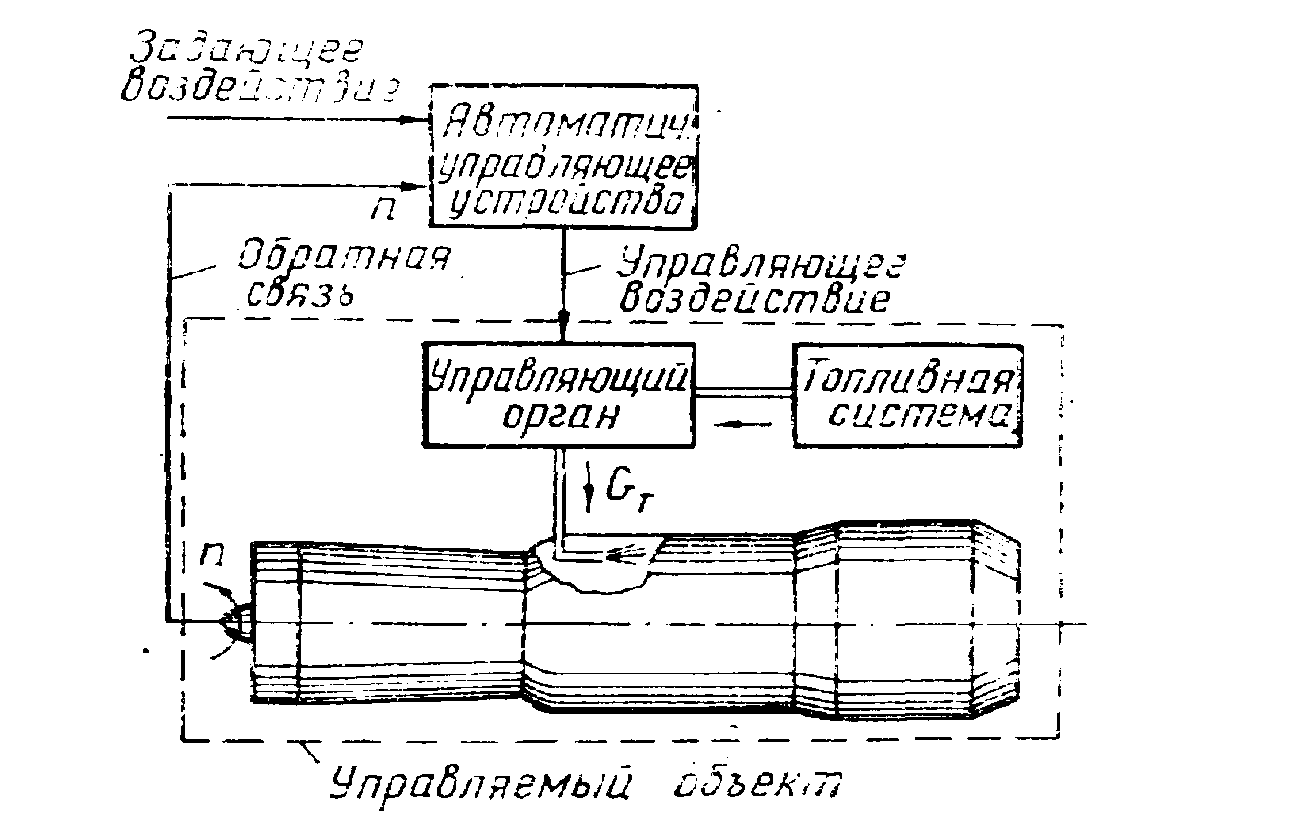
Этот принцип предусматривает измерение управляемой величины, сравнение её с заданным значением и выработку такого управляющего воздействия, которое ликвидирует отклонение истинного значения управляемой величины от заданного значения (рис.).

Характерная особенность таких САУ – наличие обратной связи, т.е. информация о состоянии ОУ передается с выхода системы на вход управляющего устройства.

Такой принцип впервые был реализован И.И. Ползуновым в регуляторе уровня воды в паровом котле (1765 г.) и Дж. Уаттом в регуляторе частоты вращения вала паровой машины (1784 г.).

Автоматические системы, реализующие принцип отклонения, называют также замкнутыми. Замкнутость контура управления осушествляется через обратную связь.

Таким образом особенностью принципа построения САУ по отклонению является замер управляемой величины. Возмущающие воздействия не замеряются, ибо в конечном итоге они сказываются на значении управляемой величины, которая контролируется АУУ.

Достоинства данного принципа:

• высокая точность поддержания управляемой величины

Недостатки:

• меньшее быстродействие по сравнению с САУ, построенными по возмущению;

• склонность к колебаниям управляемой величины. Для подавления колебаний требуется соответствующий подбор элементов системы, а иногда и постановка специальных устройств.

САУ, построенные по принципу отклонения, называют также системами автоматического регулирования.

б) На слайде № 2.2 представлена схема автоматической системы управления частотой вращения ротора ТРД. Система поддерживает управляемую (регулируемую) величину – частоту вращения ротора двигателя n в соответствии с заданным её значением n_з .Задающее воздействие, определяющее величину n_з, устанавливается с помощью рычага управления двигателя (РУД). Истинное значение частоты вращения n выдается датчиком. В зависимости от величины и знака отклонения вырабатывается управляющее воздействие, приложенное к управляющему органу. Управляющий орган изменяет подачу топлива в двигатель таким образом, чтобы последующее изменение частоты вращения ликвидировало рассогласование .

Слайд 2.2

По компенсации возмущающих воздействий

Этот принцип называют также принципом компенсации возмущений. Он предусматривает выработку управляющего воздействия в зависимости от результата измерения возмущений, действующих на объект управления (рис.).

Возмущения нежелательно изменяют управляемую величину. Управляющее воздействие позволяет компенсировать нежелательное влияние возмущающих воздействий. Учесть все возмущающие воздействия трудно, поэтому в таких САУ учитываются лишь основные возмущения, наиболее сильно влияющие на управляемую величину. Отсюда – недостаток системы:

• снижение точности поддержания управляемой величины

САУ, построенные по принципу компенсации возмущений, называются незамкнутыми, поскольку не имеют обратной связи.

Достоинства таких систем:

- более высокое быстродействие по сравнению с системами, работающими по принципу отклонения. Это является следствием того, что система реагирует непосредственно на причину, которая вызывает изменение управляемой величины, а не на следствие – само изменение управляемой величины.

• не замкнутость контура управления исключает склонность к колебаниям.

На слайде № 2.4 представлена схема системы автоматического управления частотой вращения ротора ТРД. Управляемая величина – частота вращения ротора – не измеряется, измеряются факторы, которые определяют частоту вращения ротора, т.е. полное давление воздуха перед компрессором и давление топлива перед форсунками двигателя Р_ф. Возмущающее воздействие больше всего влияет на частоту вращения ротора при неизмененной подаче топлива в двигатель. Значение Р_ф определяет расход топлива G_т – управляющий фактор системы, который в свою очередь определяет частоту вращения ротора двигателя при неизмененных возмущающих воздействиях. Для каждого значения возмущающего воздействия АУУ устанавливает такое давление Р_ф, которое обеспечивает заданное значение частоты вращения ротора. Поскольку на частоту вращения кроме действуют и другие возмущения, то делается это с некоторой ошибкой. Например, частота вращения не остается постоянной при изменении высоты полета (поскольку, кроме давления изменяется и температура.).

Слайд 2.4

Комбинированный принцип построения

систем автоматического управления

Этот принцип сочетает в себе принципы построения систем управления по отклонению и по возмущению.

Достоинства таких САУ:

- Точность работы комбинированных САУ выше точности систем, построенных на принципе компенсации возмущений.

- Большое быстродействие на переходных режимах работы системы.

Таким образом, комбинированные системы лишены недостатков, характерных для систем, реализующих либо только принцип отклонения, либо только принцип компенсации.

Недостаток: - их большая сложность.

На слайде № 2.6 представлена схема комбинированной САУ частоты вращения ротора ТРД, на которой имеются все элементы системы, работающей на принципе отклонения. Кроме того, в системе измеряется основное возмущающее воздействие . Это позволяет выработать компенсирующую поправку управляющего воздействия до того, как произойдет изменение частоты вращения ротора.

Слайд 2.6

Принцип адаптации

Этот принцип стал использоваться в САУ сравнительно недавно. САУ, использующие принцип адаптации (приспособления), способны изменять (улучшать) характеристики САУ при новых, заранее неизвестных условиях. Этот принцип используется тогда, когда исходная информация настолько мала и неопределенна, что невозможно заранее спроектировать хорошо работающую систему с фиксированными свойствами.

К адаптивным системам относятся:

• экстремальные системы

• самонастраивающиеся системы

• обучающиеся системы

Пример экстремальной системы

• система изменения километрового расхода топлива

Километровый расход топлива имеет минимум по скорости полёта V, который зависит от внешних условий, изменение которых предсказать заранее невозможно.

Функциональная схема такой САУ представлена на рис.

Задание режима полета V в такой системе осуществляется выбором тяги Р двигателя, которая определяется подачей топлива .

Основой такой системы является устройство поиска экстремума. Экстремум достигается методом пробных управляющих воздействий с оценкой направления изменения при таких воздействиях.

Для данного примера на правой ветви кривой частная производная положительна, на левой ветви – отрицательна.

В.1. Способы описания систем автоматического управления

В общем случае описание САУ содержит:

1. словесную характеристику;

2. пояснение функциональных и структурных связей с помощью специальных схем;

3. математическую запись алгоритмов работы отдельных звеньев и системы в целом.

Словесное описание

Словесное описание дает общую характеристику системы, ее основных свойств и принципа работы. Оно поясняет схемы, а также математическую запись алгоритмов. Словесное описание может сопровождаться различными графиками и таблицами.

Описание с помощью функциональных и принципиальных схем.

Структурные схемы САУ.

На функциональных схемах САУ отдельные элементы, агрегаты или узлы системы обозначаются прямоугольниками. Они снабжаются надписями с названиями соответствующих элементов. Прямоугольники соединяются линями – аналогами функциональных связей. Стрелки на линиях обозначают направление прохождения сигналов. Линии часто сопровождаются надписями, поясняющими характер сигнала. Для большей наглядности некоторые прямоугольники могут заменяться упрощенными изображениями элементов. Пример представлен на рис.

Подробность функциональных схем может быть различной. Прямоугольник может обозначать элемент системы, а может обозначать и группу элементов, объединенных решением общей задачи.

Функциональная схема САУ позволяет лишь качественно проанализировать процессы управления, определить ее состав и взаимодействие элементов при выполнении задачи управления.

Структурной схемой называется условное графическое изображение математической модели САУ. Она состоит из изображений элементов в виде прямоугольников, внутри которых записаны операторы (передаточные функции), указывающие на действия, которые нужно совершить над входным сигналом, с тем, чтобы получить выходной сигнал. На схеме стрелками указываются также все внешние воздействия и связи элементов между собой. Пример изображения элемента на структурных схемах на рис.

Структурная схема отличается от функциональной тем, что она дает полное математическое описание системы.

При изображении функциональных и структурных схем используются типовые элементы коммутации, каковыми являются:

Принципиальные схемы элементов, узлов или систем представляют собой подетальную конструктивную разработку. Они позволяют выявить состав системы, увязать взаимодействие деталей, узлов при работе системы.

Математическое описание

Математическое описание САУ представляется в виде алгоритмов работы системы и отдельных ее элементов. Алгоритмы работы записываются в виде уравнений, которые связывают управляемую величину с управляющими и возмущающими воздействиями. Алгоритмы отдельных элементов являются уравнениями связи их входных и выходных сигналов. В общем случае такие уравнения являются дифференциальными. Работу САУ на установившихся и переходных режимах можно описать, использовав уравнения отдельных элементов системы.

Решив систему уравнений всех элементов или, что то же самое общее уравнение САУ, можно определить значение управляемой величины в любой момент времени.

Основы операционного исчисления. Применение операционного

исчисления для формализации описания автоматических систем

Для описания динамических процессов в линейных автоматических системах используются обыкновенные дифференциальные уравнения с постоянными коэффициентами, имеющие вид.

(1)

где - входной сигнал,

- выходной сигнал

- некоторые постоянные коэффициенты (параметры системы).

Начальные условия для решения этих уравнений обычно принимаются нулевыми:

Для использования в автоматике удобной является операторная форма записи уравнений

(2)

где - оператор дифференцирования

Операционное исчисление позволяет значительно облегчить применение математического аппарата для исследования САУ, поскольку позволяет сводить решение линейных дифференциальных уравнений к решению алгебраических уравнений. Это достигается путем замены изучаемых функций (оригиналов) другими функциями (изображениями), получаемыми из первых с помощью преобразования Лапласа, которое переводит функцию – оригинал в функцию – изображение

где - параметр комплексной переменной.

Операцию обратного преобразования от изображения к оригиналу обозначают .

Таким образом, из дифференциального уравнения (для оригиналов) получается алгебраическое уравнение (для изображений). Решение полученного алгебраического уравнения дает изображение решения исходного уравнения. Затем по изображению с помощью обратного преобразования находится само решение (оригинал).

Для использования операционного исчисления применяются таблицы перевода оригиналов в изображение (см. слайд 3.1).

При нахождении изображений сложных функций и для обратного перехода используются следующие основные теоремы операционного исчисления.

1. Изображение суммы оригиналов функций равно сумме изображений этих функций.

Аналогичная теорема справедлива и для обратного перехода.

2. Постоянный множитель можно выносить из-под знаков операций нахождения изображения и оригинала.

.

3. При нулевых начальных условиях (если при ) операции дифференцирования оригинала соответствует умножение изображения на :

4. Аналогично, операции интегрирования оригинала соответствует деление изображения на .

В.2. Передаточная функция элемента и соединений элементов

Понятие передаточной функции является одним из основных в автоматике. Подойти к этому понятию можно и используя запись в операторной форме, и на основе операционного исчисления.

Уравнение, записанное в операторной форме (2) можно разрешить относительно выходного сигнала у(t)

Выражение перед входным сигналом является передаточной функцией и обозначается .

Передаточная функция – это функция оператора D и показывает, какие операции необходимо проделать над входным сигналом для получения выходного сигнала. Математически это записывается .

С другой стороны выражение для передаточной функции можно получить, опираясь на понятия операционного исчисления. Изображение уравнения (1) можно записать в виде

где и изображения функций и .

Действуя с последним уравнением, как с алгебраическим, получим выражение для передаточной функции.

Таким образом, передаточная функция линейной стационарной системы есть отношение изображений выходного сигнала к входному. Она связывает изображение выходного и входного сигналов.

Передаточные функции типовых соединений элементов

Последовательное соединение элементов

При таком соединении входной сигнал последовательно проходит через цепочку элементов. Входной сигнал первого элемента является входным сигналом всего соединения.

Выходной сигнал последнего элемента будет и выходным сигналом всего соединения (см. рис.3.1).

Рисунок 3.1

Передаточная функция последовательного соединения элементов равна произведению передаточных функций отдельных элементов

Параллельное соединение элементов

При таком соединении элементов на вход каждого из них подаётся один и тот же сигнал. Выходные сигналы всех элементов суммируются и образуют общий выходной сигнал соединения (см. рис.3.2).

Рисунок 3.2

Передаточная функция параллельного соединения равна сумме передаточных функций отдельных элементов.

.

Встречно – параллельное соединение

При таком соединении два элемента образуют замкнутый контур (см. рис.3.3).

а) отрицательная обратная б) положительная обратная

связь связь

Рисунок 3.3

Передаточная функция встречно – параллельного соединения имеет вид:

знак “-” – относится к положительной обратной связи, знак “+” к отрицательной обратной связи.

В.3. Статические характеристики автоматических систем

Статические характеристики устанавливают зависимости между входным и выходным сигналами на установившихся режимах.

Статические характеристики могут быть представлены либо в виде математических зависимостей, либо графически.

Математическое выражение для статической характеристики можно получить из уравнения системы, на которую воздействует входных сигналов .

(1)

На статических режимах все производные по времени равны нулю. Поэтому для таких режимов из равенства (1)получим:

(2)

Это и есть математическая запись статической характеристики. Графическое представление статических характеристик более наглядно.

На рисунке 3.4 приведены примеры статических характеристик системы управления частотой вращения n ротора ТРД от задающего (а) и возмущающих воздействий.

В качестве задающего воздействия выбран угол установки РУД ( ). Получение желательного протекания зависимости достигается настройкой системы с помощью специальных регулировочных средств.

а) по б) по Н в) по V

Возмущающими воздействиями здесь являются высоты H и скорость V полета самолета. Всегда желательно, чтобы возмущающие воздействия не влияли на величину n, поддерживаемую системой. Реальные же системы чаще всего поддерживают заданное значение управляемой величины с некоторой ошибкой (статические системы). Поля статических ошибок заштрихованы.

Графическое представление статических характеристик обладает тем недостатком, что на одном графике можно представить изменение только двух параметров при неизменном значении остальных.

Основным параметром статической характеристики является коэффициент усиления. Коэффициентом усиления К называется параметр, показывающий во сколько раз усиливается входной сигнал, пройдя через систему управления. Размерность коэффициента усиления равна отношению размерности выходного и входного сигналов.

Из равенства (2) следует, что для различных входных сигналов

Графическое толкование коэффициента усиления . В общем случае .

Статическую характеристику системы можно найти по статическим характеристикам ее отдельных элементов. При аналитическом задании статических характеристик для этого достаточно из системы уравнений элементов исключить промежуточные параметры. При графическом задании статических характеристик элементов необходимо графическое перестроение как показано на рис.3.5: а) – для параллельного и б) последовательного соединения элементов.

а) б)

В.4. Динамические характеристики автоматических систем

Динамические характеристики определяют поведение системы на неустановившихся режимах. Они являются более общими по уравнению со статическими характеристиками. Статические характеристики можно рассматривать как частный случай динамических характеристик.

Неустановившимся режимам свойственно изменение по времени входных и выходных сигналов. Их называют еще переходными режимами (переходными процессами).

Динамические свойства системы полностью определяются ее дифференциальным уравнением или же передаточной функцией и оцениваются по ее реакции на некоторые типовые воздействия, которыми являются:

а) Единичная ступенчатая функция 1(t) равна единице при и нулю при .

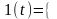
В операционном исчислении единичной ступенчатой функции соответствует изображение 1/р.

б) Единичная импульсная функция , называемая дельта функцией. По определению – функция равна;

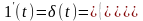
а) строгое изображение б) изображение

Единичную импульсную функцию можно рассматривать как прямоугольный импульс продолжительностью и высотой 1/ , когда . Площадь такого импульса равна единице. Изображением единичной импульсной функции является единица.

Между единичной функцией и единичной импульсной функцией существует следующая связь

в) Гармоническая функция

где А – амплитуда;

- круговая частота;

- начальная фаза;

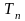- период колебаний;

смещение по времени фиксируемого начала колебаний.

В автоматике чаще используется гармоническая функция, записанная в комплексной форме.

Это равенство называется формулой Эйлера и графически представляется

Для оценки различных автоматических систем кроме одинаковых сигналов, подающихся на вход, важно иметь и одинаковые начальные условия.

В автоматике чаще всего используются нулевые начальные условия:

а) для уравнений, записанных в абсолютных величинах при t=0.

, где

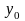- значение параметра на установившемся режиме.

б) для уравнений, записанных в отклонениях от исходного установившегося режима при

.

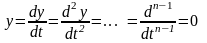Переходной функцией называется изменение по времени выходного сигнала автоматической системы при подаче на ее вход входного сигнала в виде единичной ступенчатой функции.

Переходную функцию звена будем обозначать , системы Переходную функцию элемента или системы можно получить решением соответствующего уравнения, если положить в нем входной сигнал равным . Однако проще для этого использовать аппарат операционного исчисления. Поскольку изображение единичной ступенчатой функции равно 1/р, то для отыскания изображения переходной функции необходимо разделить передаточную функцию на .

, где - изображение переходной функции. Оригинал – сама переходная функция – находится с помощью таблицы.

Импульсной переходной функцией называется изменение по времени выходного сигнала при подаче на вход единичной импульсной функции. Она обозначается g(t), ее также называют весовой функцией. С использованием операционного исчисления, учитывая, что изображение единичной импульсной функции равно единице, получим , где - изображение импульсной переходной функции.

Таким образом, для нахождения импульсной переходной функции необходимо, рассматривая передаточную функцию как ее изображение, отыскать оригинал по таблице.

Между переходной и импульсной переходной функцией существует взаимосвязь

.

Переходные функции имеют аргументом время, поэтому их называют также временными характеристиками.

В.5. Частотные характеристики автоматических систем

Частотные характеристики можно получить экспериментально и теоретически решением дифференциального уравнения.

При экспериментальном получении частотных характеристик на вход системы подается гармонический сигнал различной частоты от до . При этом после установления режима колебаний на выходе системы получается гармонический сигнал той же частоты, что и на входе, но иной амплитуды и фазы.

Частотная характеристика – это зависимость амплитуды и сдвига фазы колебаний выходного сигнала от частоты колебаний входного сигнала.