Слайд 12.4

Принципиальная схема гидромеханической

цепи – последовательно подключаемого

корректирующего устройства

Она включает параллельные соединённые ёмкость 1 и сопротивление (дроссель) 4. В ёмкость помещён поршень 3, имеющий пружины 2 с обеих сторон. Будем считать координату при нейтральном положении поршня ( ).

Пренебрегая силами трения, инерции и сжимаемостью жидкости можно записать.

(2)

(3)

(4)

(5)

, (6)

где - площадь поршня;

- площадь дросселя;

- коэффициент пропорциональности;

- жёсткость пружины.

Подставим в (3) значения и из (4) и (5), предварительно исключив из (4) с помощью (6). Тогда полученную зависимость можно представить:

, где (7)

Проанализируем равенство (7). В статике .

Поэтому и корректирующая цепь как бы отсутствует. Корректирующая связь передаёт входной сигнал на выход без искажения.

На неустановившихся режимах . При этом выходное давление изменяется медленнее, чем входное (член с справа в (7)), т. е. выходной сигнал по сравнению с входным ослабляется. Доля ослабления сигнала за счёт определяется пропускной способностью дросселя .

При очень большой производительности дросселя выходной сигнал не изменяется по сравнению с входным, корректирующее свойство вырождается. Если производительность дросселя равна нулю (например, при полном засорении), то цепь не пропускает основного сигнала и не может работать в системе управления.

На практике пропускная способность дросселя лежит между этими крайними значениями и подбирается так, чтобы получить нужный характер переходного процесса.

Левый канал корректирующей цепи подключается к дроссельному усилителю, а правый канал – к гидравлическому силовому цилиндру.

В целом гидропривод с таким корректирующим устройством работает примерно так же, как гидропривод с изодромной обратной связью. Однако, первый существенно проще второго в производстве и эксплуатации.

В.1. Устойчивость автоматических систем

Устойчивость – свойство системы возвращаться в исходное состояние после прекращения действия возмущения.

Понятие устойчивости имеет чёткий математический смысл. Рассмотрим его применительно к линейной автоматической системе. В такой системе связь между входным и выходным сигналами определяется линейным уравнением.

(1)

Решение этого уравнения определяется начальными условиями, характеризующими исходное состояние входного сигнала (например, при и т.д.) или выходного сигнала (например, при и т.д.).

В общем виде решение уравнения записывается как сумма общего решения однородного уравнения (левой части уравнения (1)) и частного решения общего уравнения .

(2)

Решение никак не зависит от характера входного сигнала, действующего на систему. Это решение отражает собственные свойства автоматической системы.

Решение характеризует реакцию системы на действие задающего сигнала или возмущения и является вынужденной составляющей выходного сигнала.

Для оценки устойчивости линейной системы необходимо и достаточно рассмотреть только общее решение однородного уравнения , которое определяется собственными свойствами системы. Решение однородного уравнения имеет вид

, (3)

где - корни характеристического уравнения

(4)

Для того, чтобы система управления была устойчивой, необходимо, чтобы с течением времени (после переходного процесса) решение превращалось в нуль, т.е. необходимыми достаточным условием устойчивости системы является

при (5)

Это условие выполняется тогда, когда корни характеристического уравнения или их вещественные части отрицательны.

В геометрической интерпретации все корни характеристического уравнения должны находиться в левой полуплоскости комплексной плоскости корней (слайд 13.1).

Слайд 13.1

Распределение корней на комплексной плоскости и характер

переходного процесса для автоматической системы: а –устойчивой, б – неустойчивой, в – на границе устойчивости

Если хотя бы один корень (или его вещественная часть) положителен, условие (5) не может быть выполнено и система неустойчива.

Таким образом, необходимым и достаточным условием устойчивости линейной системы автоматического управления является отрицательность вещественных частей всех корней её характеристического уравнения.

Состояние системы между устойчивым и неустойчивым положениями называется граничным. Условием граничного состояния является равенство нулю хотя бы одного корня или его вещественной части (остальные корни отрицательны). Параметры системы управления, находящейся на границе устойчивости, называются критическими.

Однако решение характеристического уравнения при затруднительно, поэтому в автоматике разработаны косвенные методы оценки знаков корней – критерии устойчивости.

В.2 Математическая оценка устойчивости систем

В.2.1 Алгебраические критерии устойчивости

Для систем управления, описываемых уравнениями первого и второго порядка, достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения.

Для обеспечения устойчивости системы, описываемой линейным дифференциальным уравнением третьего порядка, необходимо соблюдение двух условий:

1) все коэффициенты характеристического уравнения должны быть положительны.

2) Произведение средних коэффициентов должно быть больше произведения крайних .

Для определения устойчивости систем выше третьего порядка применяют критерий Гурвица, который формируется следующим образом.

Система с характеристическим уравнением (4) будет устойчива, если при специально составленный определитель из его коэффициентов (определитель Гурвица) и все его диагональные миноры положительны:

.

Определитель Гурвица составляется следующим образом:

по диагонали сверху вниз направо записываются коэффициенты:

в каждой строке вправо и влево от коэффициента, принадлежащего диагонали, записываются другие коэффициенты так, чтобы их индексы направо после убывали; вместо отсутствующих коэффициентов ставятся нули.

. ……………..

…………..…………..

………………………………..……………

…………………………..………………..…

………..

……………

... ……….

Определитель Гурвица имеет строк и столбцов. Минор является определителем, который образуется из определителя Гурвица путём вычёркивания левого столбца и верхней строки. Все последующие миноры образуются из предыдущего вычёркиванием левого столбца и верхней строки.

Если при коэффициенте один из определителей меньше нуля, то система неустойчива. Если один из определителей равен нулю, а остальные определители и положительны, то система находится на границе устойчивости.

В.2.2 Графоаналитический критерий устойчивости Михайлова

Для получения критерия Михайлова необходимо сформировать функцию , которая получается из характеристического уравнения системы заменой на мнимый параметр .

Выражение для можно представить как уравнение комплексного вектора, имеющего действительную и мнимую части.

.

Конец вектора при изменении от до опишет кривую, которая называется кривой Михайлова. Кривая начинается в точке , .

Согласно критерию Михайлова линейная система - го порядка будет устойчива, если кривая Михайлова охватывает начало координат и последовательно проходит в положительном направлении (против часовой стрелки) квадрантов, уходя в -ом квадрате в бесконечность.

Кривая Михайлова строится графически по точкам получаемым расчётом координат при различных значениях . Примеры кривых Михайлова приведены на слайде 13.3.

Слайд 13.3

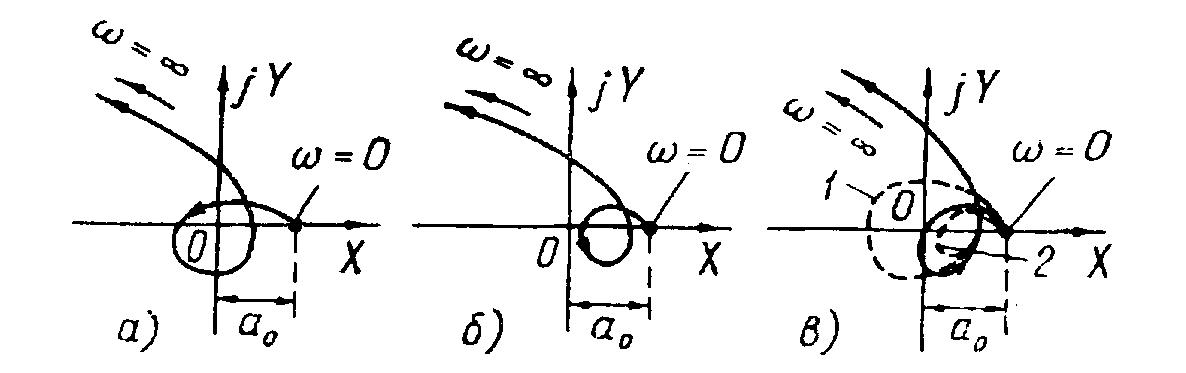
Кривые Михайлова для системы шестого порядка:

а – система устойчива; б – система неустойчива;

в – система на границе устойчивости (сплошная линия)

В.2.3 Частотные критерии устойчивости

Пусть передаточная функция разомкнутой системы .

Тогда передаточная функция замкнутой системы с отрицательной обратной связью .

Между частотными характеристиками разомкнутой и замкнутой систем существует однозначная связь, Поэтому по частотным характеристикам разомкнутой системы можно судить об устойчивости всей системы.

Выражение для амплитудно–фазовой частотной характеристики разомкнутой системы.

можно рассматривать как вектор на плоскости комплексного параметра (рис.1).

Рис. 1

При изменении от 0 до конец вектора описывает кривую – годограф амплитудно–фазовой частотной характеристики. Частотный критерий формулируется следующим образом (слайд 13.4).