10.4. Побудова діаграм навантаження.

Можливо окремо розглядати діаграму навантаження механізму Mc(t) і діаграму навантаження електропроводу M(t), яка повинна ураховувати зміну навантаження, зміну швидкості ω(t) та інші перехідні процеси, оскільки, як добре відомо .

Якщо технологічний режим не вимагає зміни швидкості та навантаження, то знаходження моменту на валу двигуна суттєво спрощується. Коли ω≈const можливо не враховувати втрати в перехідних режимах, тобто вважати, що M(t)=Mc=const і P(t)=Pc=const.

Формули для розрахунків потужності и момента механізмів відносно прості, вони дані у відповідних довідниках и розглянуті на практичних заняттях.

Більш-меньш складним є побудова навантажувальної діаграми, коли швидкість прискорення та інші показники системи змінюють під час роботи механізму.

Розглянемо побудову навантажувальної діаграми ліфта на ділянці, де він розганяється до відповідної швидкості, рухається деякий час з незмінною швидкістю, а потім його рух гальмується. При цьому швидкість ω, прискорення dω/dt і ривок обумовлені відповідними нормами. Така навантажувальна діаграма включає 7 ділянок; її побудова показана на рис 10.5

Першою будується ділянка 4, де ω=const, потім 2 та 6 з постійними прискоренням і пригальмовуванням (dω/dt=const), а швидкість змінюється за лінійним законом.

Ділянки 1, 3, 5, і 7 – це лінійна зміна прискорення, при якій ривок , а швидкість змінюється за параболічним законом.

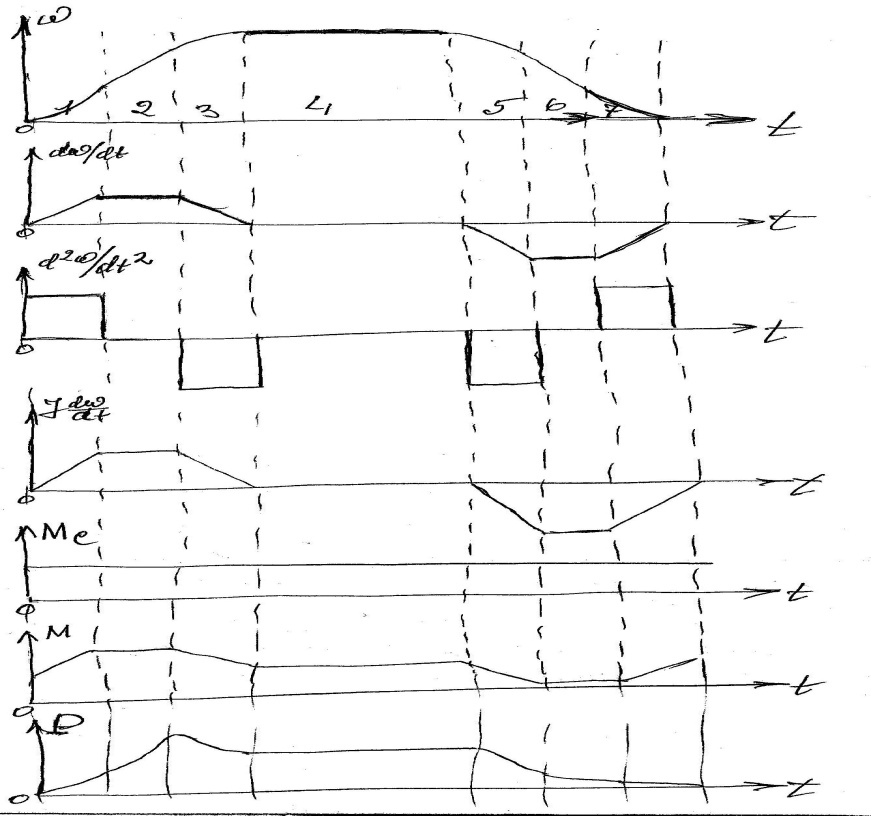
Рис. 10.5

Оскільки відомо значення моменту інерції, то можливо побудувати , а за значенням Мс(t)=const можливо побудувати графік . Нарешті за графіками М(t) и ω(t) можливо побудувати P(t), оскільки P=M ω, і приступати до вибору двигуна за потужністю.

10.5 Вибір двигуна за потужністю при режими s1.

10.5.1 Метод еквівалентних втрат потужності.

Якщо при режимі S1 Pc=const (див рис. 10.2, а) то номінальна потужність двигуна, який є вибраним Pн≥Pc. Але при тривалому режимі навантаження на валу двигуна може змінюватись і, як слід, будуть змінюватись втрати і перегрів двигуна. Згідно виразу 10.6 при збільшенні втрат потужності збільшується і температура, а при зниженні втрат – навпаки.

Коли кількість циклів роботи q, час одного циклу tц, a , то графік температур повторюється від циклу до циклу і перегрів двигуна на початку циклу і при його кінці буде однаковим, тобто τпоч.ц. = τкінц.ц.

Нехай робочий цикл двигуна має n ділянок, на кожній з котрих P=const, і Σр=const. Тому на будь-якій і-тій ділянці перегрів буде за виразом (10.5) , де за (10.3) , а - початковий перегрів на і-тій ділянці. Але також очевидно, що .

З урахуванням цих обставин, складемо систему рівнянь нагрівання:

(10.8)

У (10.8) τ0 – початковий перегрів циклу.

Якщо в системі (10.8) виключити значення перегріві у кінці кожної проміжної ділянки при i<n, то можливо визначити значення перегріву у кінці робочого циклу

Оскільки, як обумовлено раніше то

(10.9)

Як правило , тим більше , отже в (10.9) , тому використовуючи розкладання у ряд Маклорена показникових функцій вигляду , що стоять у чисельнику і знаменнику, та обмежуючись двома скадовими цього ряду, з огляду на малість інших , після перетворень отримаємо вираз для перегріву в кінці робочого циклу:

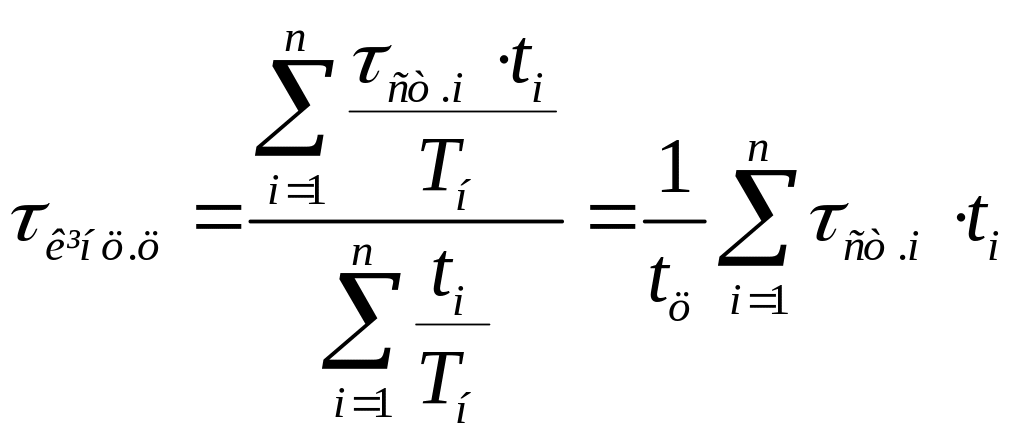(10.10)

Як слідує з (10.10) кожна з робочих ділянок може бути прийнята за початкову, тобто τкінц. ц. – є середній перегрів за цикл. Дійсно, отриманий результат (10.10) є незалежним від того, яка ділянка циклу є початковою (i=1), а яка кінцевою (i=n): з максимальними або мінімальними втратами потужності.

Згідно (10.3) в (10.10) можливо визначити , тоді одержимо

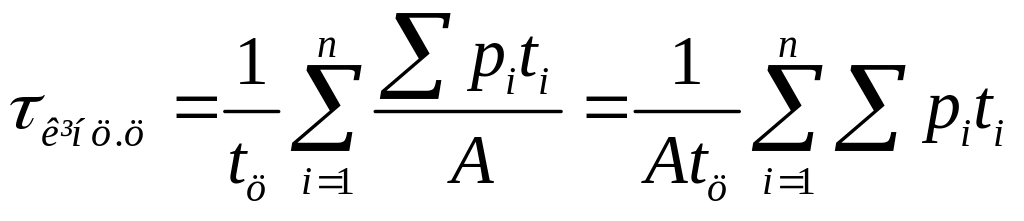(10.11)

Із (10.11) видно, що середній перегрів двигуна за робочий цикл із змінним навантаженням визначається середньою величиною втрат за цикл:

(10.12)

(10.13)

Із цього також можливо зробити важливі висновки: для визначення середнього перегріву треба знати середні втрати потужності за цикл. Середні втрати є еквівалентними змінним втратам, які спричиняють дійсний перегрів двигуна.

Тому для номінального режиму роботи справедливий вираз для допущеного перегріву:

(10.14)

Порівнявши вирази (10.13) та (10.14) одержимо, що двигун вибрано правильно, якщо:

(10.15)

У цьому разі температура двигуна вища за допустиму виключена, тому зо середні втрати за робочий цикл менші або дорівнюють втратам потужності при роботі двигуна з номінальним навантаженням.

Отримані значення справедливі в тому випадку, коли умови нагрівання і охолодження не змінюються, ω=cosnt. У протилежному випадку необхідно враховувати зміну умов тепловіддачі, оскільки постійна часу нагрівання згідно (10.3) 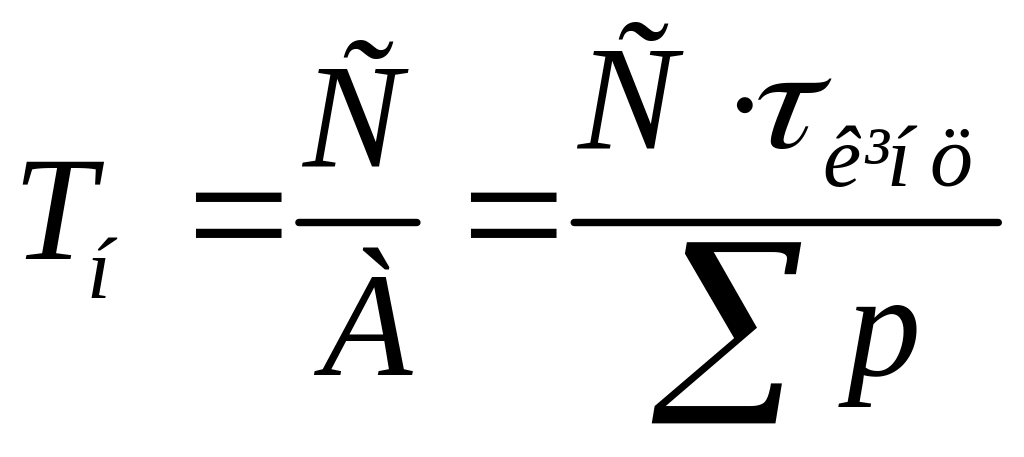, вона буде змінюватися на різних ділянках, якщо змінюється значення А, коли змінюється кутова швидкість ротора двигуна.

Можливо вважати, що коефіцієнт погіршення тепловіддачі, залежний від швидкості 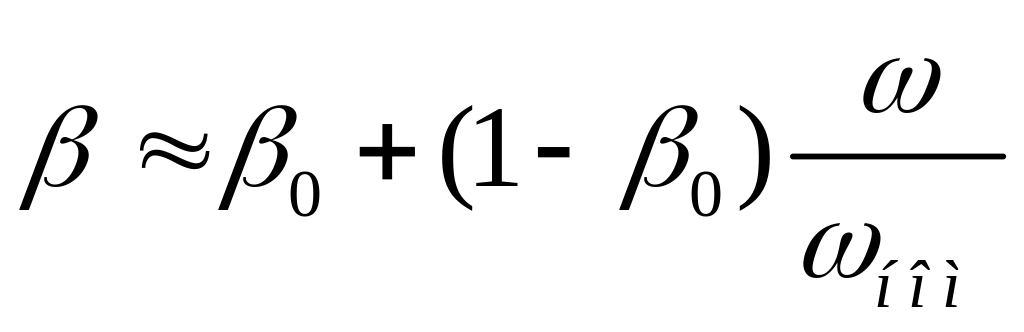, тоді на і-ій ділянці , а постійна часу . Тому це треба враховувати у виразах (10.11)…(10.13), у цьому випадку:

(10.14)

В 10.14 величина 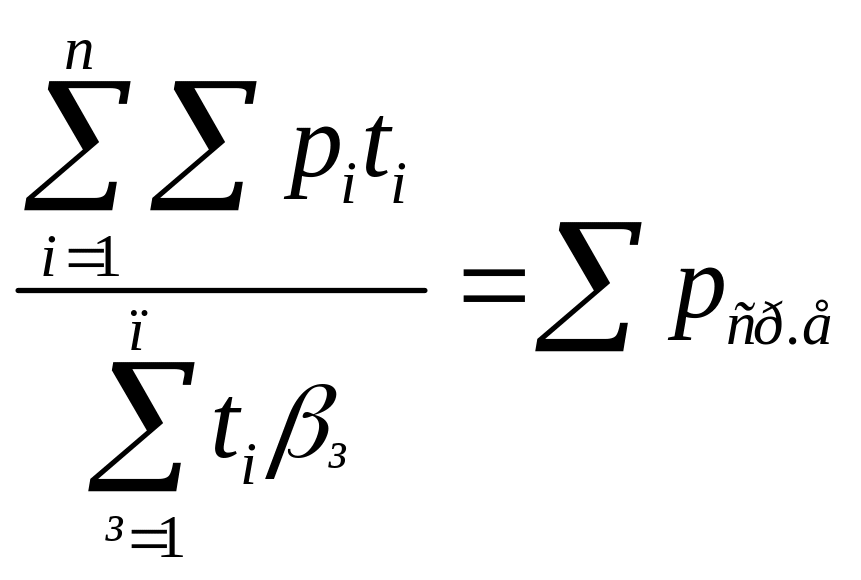- є середні еквівалентні втрати потужності з урахуванням погіршення тепловіддачі на деяких ділянках. Вираз (10.14) буде перетворений і одержить вигляд:

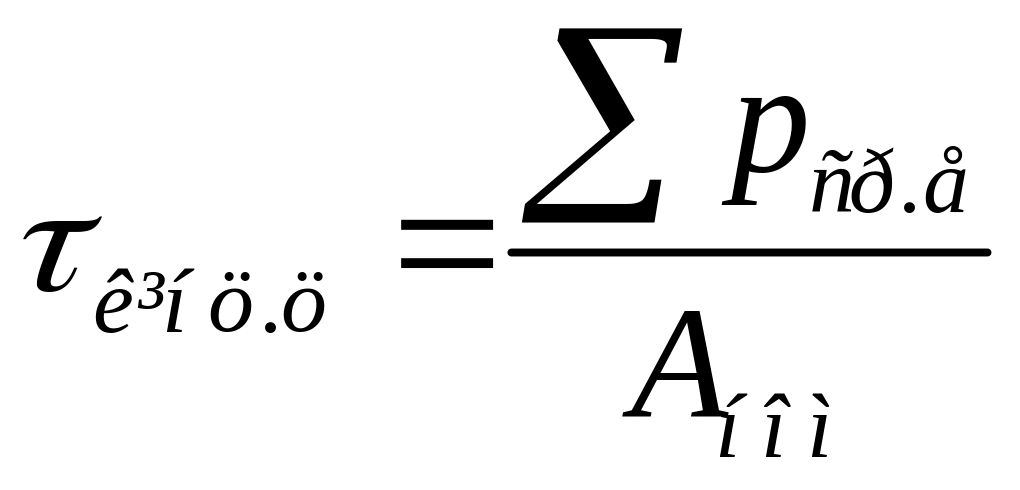(10.15)

Оскільки , то . Таким чином, в цьому випадку еквівалентні втрати будуть більшими за середні втрати. Додамо, що коли температура навколишнього середовища перевищує 40 °С, слід зменшити витрати потужності, зменшуючи навантаження на двигун.

Розглянутий метод середніх втрат потужності є найбільш точним і універсальним методом перевірки вже вибраного двигуна за нагріванням. Але для його застосування необхідно знати параметри двигуна, щоб визначити втрати на кожній ділянці робочого циклу, що не завжди можливо.