2. Правая запись.

a=b, b=c. Тогда ,

Мы будем пользоваться левой записью (отметим, что в книге [1] используется правая).

Произведение отображений ниже мы будем обозначать через .

Замечание 1. Из определения умножения отображений следует, что перемножать можно не любые отображения, а только те, у которых «средние» множества одинаковые. Например, если , то при В=D можно перемножать отображения f и φ, а при В≠D нельзя.

Свойства умножения отображений

Определение 2. Отображения f и g называются равными, если у них совпадают области определения и области значений, т.е. и выполняется условие: справедливо равенство .

1. Умножение отображений некоммутативно. Другими словами, если fφ и φf существуют, то они не обязательно равны.

Пусть, например, множества A=B=C=R, , .

Рассмотрим произведения:

Следовательно, функции fφ и φf различны.

2. Умножение отображений ассоциативно.

Пусть . Докажем, что и существуют и равны,т.е. = . (1)

Очевидно, что .

Для доказательства равенства (1) в силу определения равенства отображений требуется проверить, что (2). Пользуясь определением умножения отображений (в левой записи) имеем:

, (3)

(4)

Т.к. в равенствах (3) и (4) равны правые части, то равны и левые, т.е. справедливо равенство (2), а тогда выполняется и (1).

Замечание 2. Ассоциативность умножения позволяет однозначно определить произведение трех, а затем и любого конечного числа множителей.

3. Обратное отображение. Пусть отображение , .

Можно ли определить обратное отображение ? Не всегда, т.к. у элемента b может быть несколько прообразов в А, либо вообще не быть прообразов. Однако для биективного отображения f обратное определить можно.

Пусть – биекция, . Тогда для любого элемента по определению биекции существует единственный прообраз при отображении f – это элемент а. Теперь можно определить , полагая . Нетрудно видеть, что – биекция.

Итак, у всякого биективного отображения имеется обратное.

§3. Преобразования множеств

Всякое отображение называется преобразованием множества А. В частности, любая функция действительной переменной является преобразованием множества R.

Примерами преобразований множества точек плоскости служат поворот плоскости, симметрия относительно оси и т.д.

Так как преобразования – это частный случай отображений, то для них справедливо всё сказанное выше об отображениях. Но умножение преобразований множества А имеет и специфические свойства:

1. для любых преобразований f и φ множества А произведения fφ и φf существуют;

2. существует тождественное преобразование множества А .

Нетрудно видеть, что для любого преобразования f этого множества , так как, например, . Значит, преобразование  играет роль единичного элемента при умножении преобразований.

3. Если f – биективное преобразование множества А, то существует 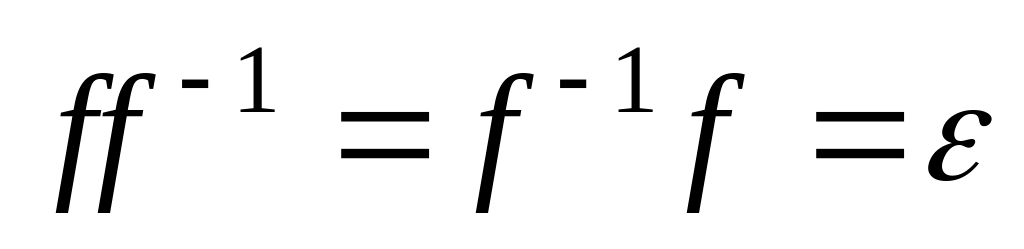и . Эти равенства легко проверяются. Тем самым обратное преобразование играет роль обратного элемента при умножении преобразований.