§3. Однородные симметрические многочлены

Определение 6. Многочлен от n неизвестных называется однородным степени m, если все его члены имеют одну и ту же степень m.

Нетрудно видеть, что любой многочлен можно представить в виде суммы однородных многочленов, поэтому, чтобы научиться выражать симметрический многочлен через элементарные симметрические многочлены, достаточно уметь это делать для однородных симметрических многочленов.

Пусть f – однородный симметрический многочлен с высшим членом , k₁+k₂+…+k_n= m. Тогда f – однородный многочлен степени m. Нетрудно видеть, что многочлены f_j, появляющиеся при доказательстве основной теоремы, тоже будут однородными многочленами степени m, так как _i – однородные многочлены степени m. Это значит, что в (7) l₁+l₂+…+l_n=m.

Учитывая это, можно сформулировать следующий алгоритм для выражения однородного симметрического многочлена f через элементарные симметрические многочлены:

1. выписываем высший член многочлена f;

2. находим сумму k₁+k₂+…+k_n=m;

3. из высшего члена f выписываем набор показателей k₁,k_2,…,k_n;

4. составляем всевозможные наборы l₁,l₂,…,l_n, l_jN0, 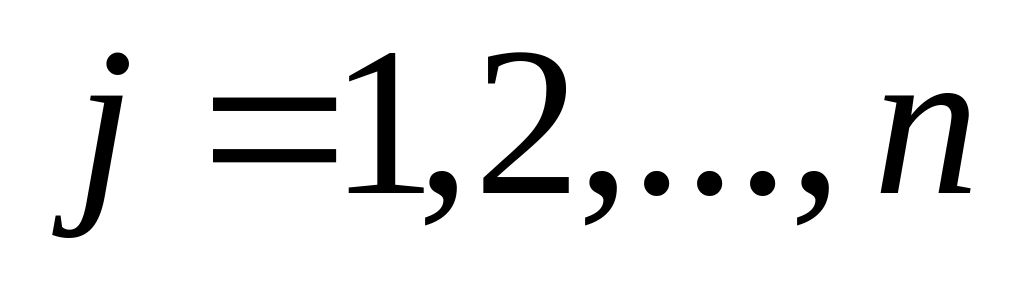, удовлетворяющее условиям:

а) l₁...l_n (для того, чтобы член мог быть высшим членом промежуточного симметрического многочлена f_j);

б) l₁ k₁, чтобы член был ниже члена ;

в) l₁+l₂+…+l_n=m.

Для каждого найденного выше набора l₁,...,l_n составляем многочлен вида , где c_i – неизвестное число. Затем записываем f в виде суммы полученных многочленов f=φ₁+φ₂+ φ_s (8), где s – число составленных в п. 4) наборов. Коэффициенты c_i находим из системы уравнений, которая получится, если придавать неизвестным х₁,…,х_n определенные наборы значений.

Замечание. Описанным выше методом неопределенных коэффициентов можно пользоваться ввиду единственности выражения симметрического многочлена через элементарные симметрические многочлены.

Часто приходится решать рассмотренную в этом параграфе задачу для частного вида однородных многочленов – моногенных многочленов.

Определение 6. Симметрический многочлен от неизвестных х₁,…,х_n , все члены которого могут быть получены из высшего члена путем всевозможных перестановок неизвестных, называется моногенным многочленом.

Если  высший член моногенного многочлена, то этот многочлен обозначается через S( ) или

Примеры. х₁х₂+ х₁х₃+ х₂х₃, х₁^k+ х₂^k+… х_n^k (степенная сумма).

§4. Значение симметрического многочлена от корней уравнения

Пусть задано уравнение вида a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n=0 (9);где a₀ ≠0, , Р – поле, и симметрический многочлен f(х₁,…,х_n). Требуется найти f(х₁⁰,…,х_n⁰), где {х₁⁰,…,х_n⁰} – все корни данного уравнения.

Эту задачу можно решать так:

1. Получим из данного уравнения приведенное уравнение (разделив его на а₀):

xⁿ+b₁x^n-1+…+b_n-1x+b_n=0.

Очевидно, что корни этого уравнения те же, что и у данного (9).

2) Используем теорему Виета:

х₁⁰+…+х_n⁰= -b₁,

х₁⁰х₂⁰+…+х_n-1⁰х_n⁰= b₂,

. . . . . . . . . . . . . . . . .

х₁⁰…х_n⁰= (-1)ⁿb_n.

Если ввести обозначения _i⁰= _i(х₁⁰,…,х_n⁰), i=1,...,n, то эти равенства перепишутся так:

₁⁰=-b₁,

₂⁰= b₂, (10)

. . . . . . . . .

_n⁰= (-1)ⁿb_n.

Мы нашли значения ₁⁰ ,… _n⁰ элементарных симметрических многочленов от корней данного уравнения.

3) Симметрический многочлен f выразим через элементарные симметрические многочлены: f(х₁,…,х_n)= (₁ ,…, _n ). Если сюда подставить корни уравнения (9) и учесть (10), то получим f(х₁⁰,…,х_n⁰)= (₁⁰,…,_n⁰)= (-b₁,b₂,…,(-1)ⁿb_n).

Задача решена.

Таким, образом, не находя корней уравнения n-ой степени от одного неизвестного (что обычно невозможно сделать при n5), мы можем вычислить значение любого симметрического многочлена от этих корней.