§5. Точечно-векторные евклидовы пространства. Группы и геометрии

Определение 13. Если аффинное пространство А связано с евклидовым пространством , то А называют точечно-векторным евклидовым пространством.

Репер в таком пространстве обычно берут ортонормированным: – ортонормированный базис (такую систему координат часто называют прямоугольной). Если в таком репере заданы координаты точек и : , , тогда . Так как вектор задан координатами в ортонормированном базисе, то .

Определение 14. Длину вектора называют расстоянием между точками и .

Таким образом, мы получили формулу для нахождения этого расстояния.

Так как любое конечномерное действительное линейное пространство можно превратить в евклидово, то любое конечномерное аффинное пространство над полем можно превратить в точечно-векторное евклидово пространство.

Пусть Д – точечно-векторное евклидово пространство.

Определение 15. Отображение Д Д называют движением, если любая точка Д, имеющая в некотором ортонормированном репере координаты ( ), переходит при этом отображении в точку с теми же координатами в другом ортонормированном репере.

Отсюда следует, что движение – это частный случай аффинного преобразования. Поэтому в ортонормированном репере записывается в виде , где – матрица перехода от ортонормированного базиса к ортонормированному; поэтому – ортогональная матрица.

Отметим, что из определения движения легко получается, что при движении сохраняются расстояния между точками. Можно доказать, что это свойство равносильно определению 15 (часто его берут в качестве определения движения).

Легко проверяется, что движения точечно-векторного евклидова пространства также составляют группу (группу движений). В ней можно выделить 2 подгруппы – вращений и переносов:

1) (когда ) – вращения (подгруппа вращений);

2) – переносы (подгруппа переносов или трансляций).

Из теоремы 4 следует, что всякое движение есть произведение вращения и переноса.

Группы и геометрии

В соответствии с точкой зрения, ставшей общепринятой более 125 лет назад и впервые четко изложенной в «Эрлангенской программе» Ф.Клейна (1872г.), под геометрией следует понимать совокупность инвариантов данной группы . Пусть – некоторое множество, или, как мы ещё будем говорить, пространство точек, – какая-то подгруппа в группе всех биективных отображений . Предметом геометрии, отвечающей , является изучение тех свойств пространственных фигур (или пространственных конфигураций точек) в , которые остаются неизменными при действии преобразований из .

Так, аффинная геометрия – инварианты группы аффинных преобразований аффинного пространства; метрическая геометрия – инварианты группы движений точечно-векторного евклидова пространства.

Если взять любое тело (фигуру) и рассмотреть все движения трехмерного пространства (плоскости) после которого это тело (фигура) переходит в себя, то они составляют подгруппу группы движений – группу симметрий тела (фигуры).

Глава 5. Квадрики §1. Квадрики в аффинных пространствах

Определение 1. Множество точек -мерного аффинного пространства А , координаты которых удовлетворяют в выбранном репере уравнению второй степени вида , (1)

где , , , называют гиперповерхностью второго порядка, или квадрикой.

Отметим, что в уравнение квадрики обязательно входит ненулевая квадратичная форма .

Ниже мы будем рассматривать только квадрики над полем действительных чисел (действительные квадрики).

В двумерном аффинном пространстве квадрики – это линии второго порядка, в трехмерном – поверхности второго порядка.

Как и в аналитической геометрии, для линий и поверхностей второго порядка здесь рассматривают взаимное расположение прямой и квадрики, асимптотические направления, центр, диаметральные плоскости и диаметры квадрик, а также вопросы, связанные с упрощением уравнений квадрик и их классификацией. Мы остановимся лишь на упрощении уравнений квадрик и на их аффинной и метрической классификациях.

Известно, что существует невырожденное линейное преобразование переменных :

, , (2) ,

приводящее действительную квадратичную форму

к нормальному виду , где , – некоторое натуральное число, не превосходящее (ранг квадратичной формы).

Преобразование переменных (2) можно рассматривать как преобразование координат, так как алгебраически они записываются одинаково. Подставив выражения для из (2) в левую часть уравнения (1), приведем это уравнение к виду . (3)

Уравнение (3) – это уравнение той же квадрики в другом репере. Покажем, что если 0, то выделением полного квадрата по и пе­реносом начала координат в уравнении (3) можно избавиться от одного слагаемого первой степени. Действительно, в этом случае сумму можно представить в виде

.

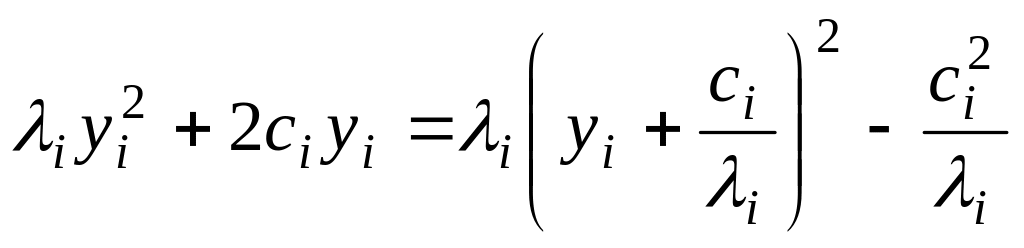Полагая при , из (3) получим уравнение, в котором коэффициент при оста­нется равным , а члена с первой степенью не будет (для данного ). Проделав такую процедуру со всеми переменными в уравнении (3), приведем это уравнение к виду

. (4)

Отметим, что если некоторое входило в (3) только в квадрате, то мы его просто переобозначили через ( ).

Рассмотрим все возможные случаи относительно коэффициен­тов и в уравнении(4):

1.Все коэффициенты нулевые, а .

Тогда уравнение (4) можно записать в виде , где .

Так как , то в существует .

Совершая далее преобразование координат по формулам ,

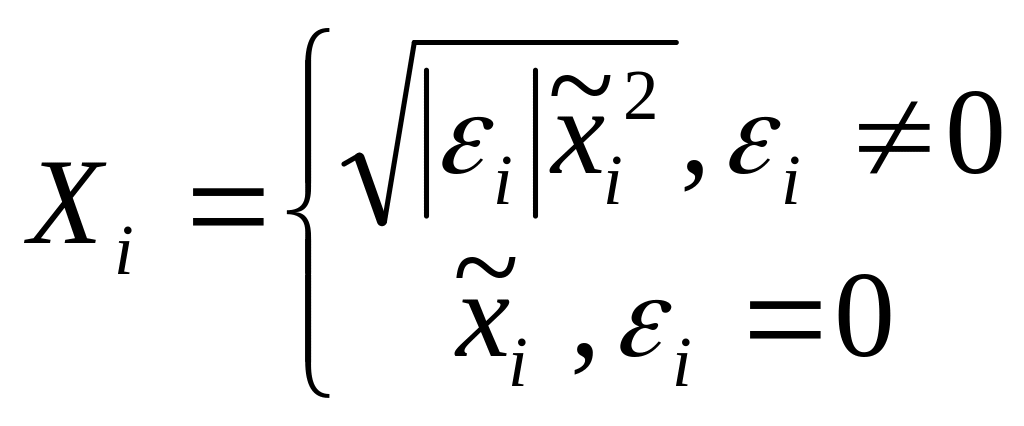последнее уравнение приведем к виду

, (5)

где и .

2. В уравнении (4) все и .

Тогда, полагая ,

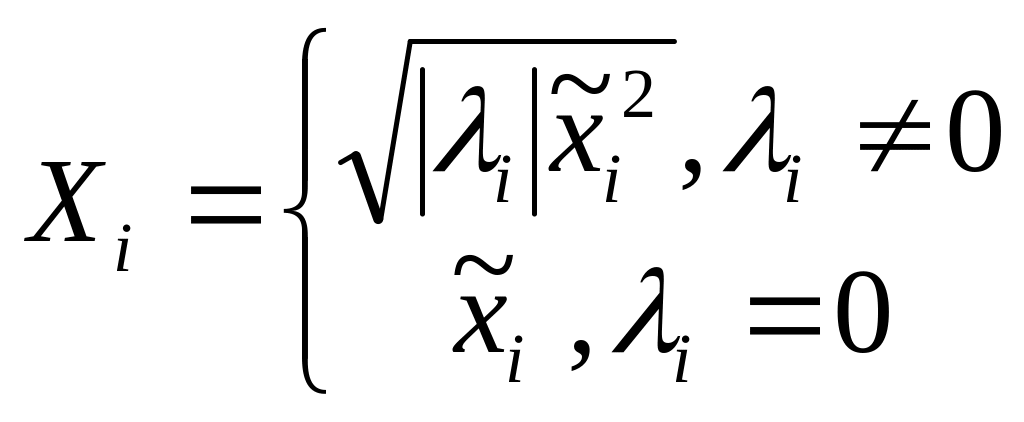уравнение (4) приведем к виду

, (6)

где и .

3. В уравнении (4) среди коэффициентов , есть отличные от нуля.

Тогда, полагая: 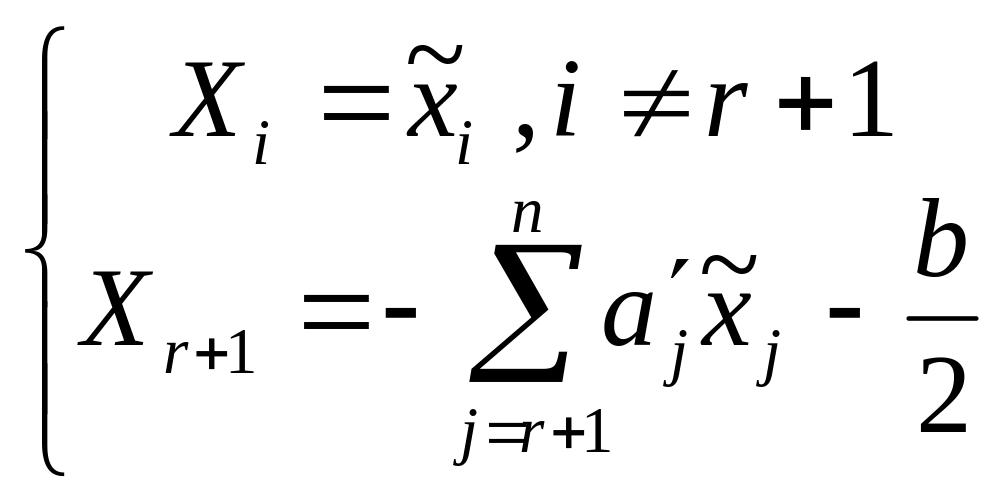, (7)

уравнение (4) приведем к виду

(8), где — натуральное число, меньшее .

Так как , то получаем два типа:

, (9)

. (10)

Мы получили все возможные канонические уравнения квадрик: (5), (6), (9), (10).

Они определяют следующие аффинные классы квадрик в :

1) если в уравнении (5) и все , то это эллипсоид

2) если в уравнении (5) и все , то имеем мнимый эллипсоид

3) если в уравнении (5) и – разных знаков, то это гиперболоид

4) уравнение (6) при определяет конусы , где . Если все имеют одинаковые знаки, то будет мнимый конус, если же среди них встретятся числа разных знаков, то будет действительный конус

5) при получим конические цилиндры;

6) при уравнение (8) определяет парабо­лоиды: (9) — эллиптический, (10) – гиперболический;

7) при уравнение (5) определяет эллиптические и гиперболические цилиндры в зависимости от того, оди­наковые или разные знаки у коэффициентов ;

8) при уравнение (6) определяет параболи­ческие цилиндры.

Замечание. Аффинные классы поверхностей 1 – 4 и 6 являются основными; оставшиеся три класса (5, 7 и 8) повторяют основные в подпространствах меньшей размерности.

Из полученных результатов непосредственно вытекают известные в аналитической геометрии аффинные клас­сификации линий второго порядка на плоскости и поверхностей второго порядка в пространстве.

Мы доказали, что в конечномерном действительном аффинном пространстве существуют 8 аффинных классов квадрик.

Можно показать, что никакие две квадрики разных классов или из одного класса, но с разными параметрами или нельзя перевести друг в друга аффинным преобразованием, т.е. такие квадрики в аффинной геометрии различны.