§3. Плоскости в аффинных пространствах

Пусть задана некоторая система линейных уравнений с коэффициентами из поля .

Определение 7. Будем говорить, что множество точек Д А (или векторов из ) удовлетворяет этой системе, если их координаты в некотором репере А (базисе ) удовлетворяют этой системе.

Известно, что если дана некоторая неоднородная система линейных уравнений с неизвестными и её приведенная однородная система, то

1) множество всех решений этой однородной системы является подпространством линейного пространства ;

2) если – частное решение неоднородной системы, то + есть общее решение неоднородной системы.

Если , то можно считать координатами некоторой точки в репере -мерного аффинного пространства А над полем .

Мы видим, что данной неоднородной системе удовлетворяют все точки аффинного пространства А, записанные в виде + , где А, – некоторое подпространство , и только эти точки.

Заметим, что если – двумерное подпространство , то + – это плоскость в трехмерном пространстве.

В связи с этим естественно обобщить понятие плоскости для любого аффинного пространства.

Определение 8. Пусть А – аффинное пространство, – некоторое подпространство и dim = , . Множество точек из А, для которых вектор принадлежит , т.е. множество, описываемое уравнением

, (3) где , , называется -мерной плоскостью.

Точка называется начальной точкой плоскости ,точка – текущей её точкой, подпространство – направляющим подпространством этой плоскости.

Из определения 8 видно, что .

Можно показать, что всякая -мерная плоскость в аффинном пространстве А сама является аффинным пространством размерности .

Отметим, что при =0 (нульмерная плоскость) получается точка . Поэтому каждую точку аффинного пространства можно рассматривать как нульмерную плоскость. Само аффинное пространство является -мерной плоскостью. Одномерную плоскость называют прямой, ( -1)-мерную плоскость – гиперплоскостью. В трехмерном пространстве это будет, как нетрудно видеть, плоскость.

В определение плоскости введена её начальная точка. Можно показать, что в качестве начальной точки плоскости можно взять любую её точку. Из этого следует, что две плоскости, имеющие одну общую точку и одно и то же направляющее подпространство, совпадают.

Пусть в аффинном пространстве А выбрана система координат , где А, – базис линейного пространства свободных векторов, и дана -мерная плоскость , проходящая через точку с направляющим подпространством (где – базис ).

Тогда , и рассматриваемую плоскость можно записать в виде

, (4)

где – параметры, принимающие произвольные числовые значения из поля независимо друг от друга.

Определение 9. Уравнение (2) называют параметрическим уравнением рассматриваемой плоскости в векторной форме.

Пусть в выбранной системе координат

.

Тогда, переходя от векторного равенства к покоординатным равенствам, получим систему уравнений

(5)

Определение 10. Систему (5) называют параметрическими уравнениями -мерной плоскости, проходящей через точку в направлении пространства .

В частном случае =1 -мерная плоскость есть прямая. При этом подпространство порождается одним вектором с координатами , а параметрические уравнения прямой (4) принимают вид

(6)

При на прямой (6) выделяется луч, а при – отрезок.

От параметрических уравнений прямой (6) легко перейти к ее каноническим уравнениям

. (7)

Исключив из параметрических уравнений (5) -мерной плоскости все параметры, получим ее общие уравнения

(8)

В частности, гиперплоскость, соответствующая случаю , задается одним уравнением

.

В системе уравнений (8) каждое отдельное можно рассматривать как уравнение гиперплоскости, а всю систему уравнений – как определение -мерной плоскости пересечением гиперплоскостей. Это наглядно иллюстрируется на примере прямых в трехмерном пространстве, так как любая такая прямая может рассматриваться как пересечение двух плоскостей.

Получив уравнение прямых и плоскостей в аффинном пространстве, можно решать все вопросы аналитической геометрии относительно прямых и плоскостей в этом пространстве, точнее вопросы относительно прямых и плоскостей, не связанные с измерением длин и углов. В частности, здесь можно развить теорию выпуклых множеств и выпуклых многогранников, нужную для линейного программирования.

Определение 11. Будем говорить, что некоторая система линейных уравнений с неизвестными с коэффициентами из задает плоскость , если этой системе удовлетворяют координаты всех точек из в некотором репере, и только они.

Из сказанного следует, что справедлива следующая теорема.

Теорема 2. Совместная система линейных уравнений с неизвестными над полем задает некоторую -мерную плоскость в аффинном пространстве А, причем = , где – ранг системы.

Замечание. Из теоремы 2 следует, что в трехмерном аффинном пространстве всякая система линейных уравнений ранга 1 задает плоскость, а ранга 2 – прямую.

Справедливо утверждение, обратное теореме 2.

Теорема 3. Любая -мерная плоскость -го аффинного пространства А с направляющим подпространством может быть задана системой ( ) линейно независимых уравнений.

Доказательство. Известно, что любое -мерное подпространство -мерного линейного пространства над может быть задано однородной системой ( ) линейно независимых уравнений (9) (т.е. координаты любого вектора из в некотором базисе и только этих векторов удовлетворяют этой системе уравнений). По определению плоскости, если – начальная точка плоскости , то тогда и только тогда, когда . Если имеет в выбранном репере координаты , - , то – координаты . Подставляя в (9) вместо выражения , получаем , или

(10) , , где .

Уравнения (10) линейно независимы и им удовлетворяют координаты всех точек из и только они, т.е. (10) – уравнения плоскости .

Теорема доказана.

Следствие. В трехмерном пространстве всякая плоскость задается одним уравнением, а всякая прямая – двумя линейно независимыми уравнениями.

Замечание. Из того, что всякая плоскость задается системой линейных уравнений и обратного утверждения (теоремы 2 и 3) легко получается:

1. пересечение любых плоскостей и 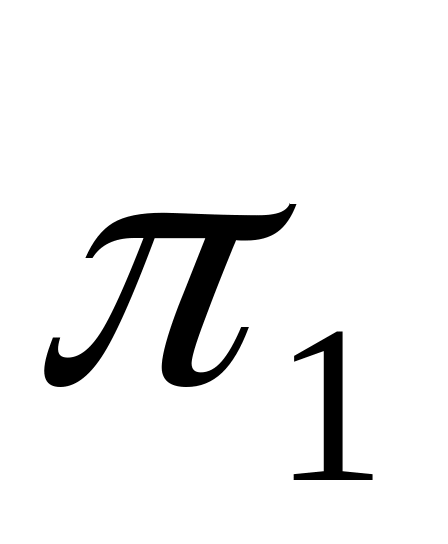аффинного пространства А – плоскость (так как это пересечение задается объединением систем линейных уравнений, задающих и );

2. всякая плоскость есть пересечение гиперплоскостей (так как последние задаются одним уравнением: гиперплоскость , dim = 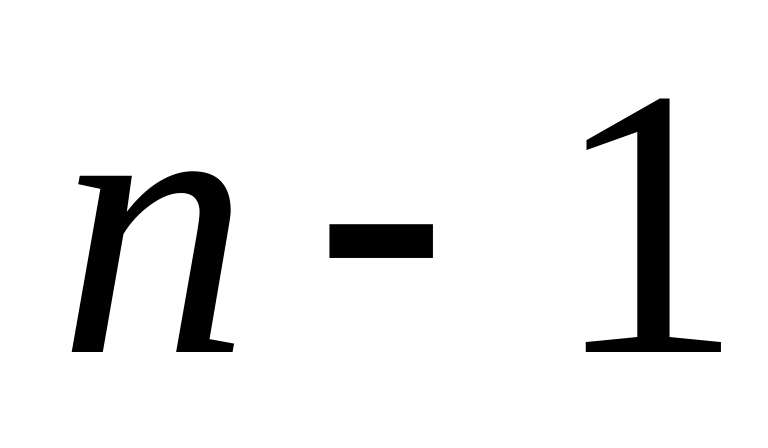, задается ( -( ))=1 уравнением ).
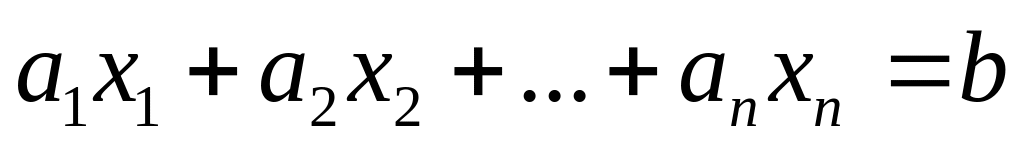