Положительно определенные квадратичные формы

Определение 9. Квадратичная форма , заданная на действительном линейном пространстве , называется положительно определенной, если для любого .

Теорема 6. Действительная квадратичная форма на -мерном линейном пространстве положительно определенная тогда и только тогда, когда её действительный нормальный вид таков:

(39) (т.е. в нем нет квадратов с коэффициентами 0 и –1; другими словами, ранг и её положительный индекс равны ).

Необходимость. Пусть – положительно определенная квадратичная форма. Будем доказывать от противного: пусть в её ДНВ существует квадрат с коэффициентом (–1) или 0. Тогда

(40) либо (41)

(виды (40) и (41) – в некотором базисе линейного пространства ).

Рассмотрим вектор , у которого координаты в этом базисе таковы: , а остальные равны 0, т.е. : . Тогда в силу (40) и (41) либо , либо , т.е. , что вступает в противоречие с определением положительно определенной квадратичной формы (ибо ). Значит, имеет ДНВ (39).

Достаточность. Пусть (39) – действительный нормальный вид в некотором базисе . Тогда с координатным столбцом в этом базисе имеем: (ибо ). Значит, – положительно определенная квадратичная форма.

Замечание 7. С помощью этой теоремы не очень удобно определять, будет ли положительно определенной (надо приводить её к ДНВ).

Есть более удобный способ.

Определение 10. Пусть 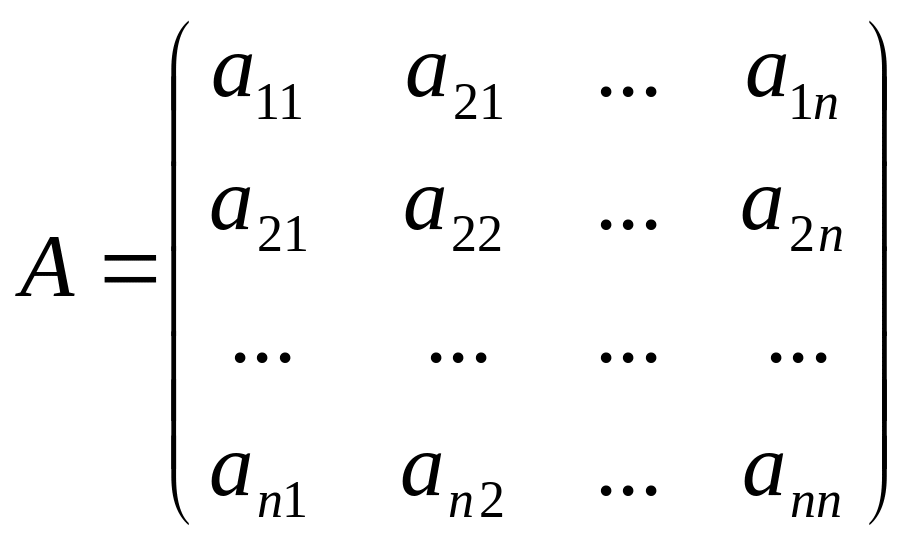– некоторая квадратная матрица. Её миноры 1-го, 2-го,…, -го порядка, расположенные в левом верхнем углу, называются главными минорами матрицы .

Если – матрица квадратичной формы , то главные миноры матрицы называются главными минорами .

Теорема (критерий Сильвестра). Действительная квадратичная форма является положительно определенной тогда и только тогда, когда все её главные миноры больше нуля.

Доказательство этой теоремы можно найти в любом учебнике линейной алгебры. Здесь мы его не приводим.

Определение 11. Квадратичная форма , заданная на линейном пространстве , называется отрицательно определенной, если .

Если отрицательно определенная форма, то, очевидно, – положительно определенная квадратичная форма, т.е.

– действительный нормальный вид , а тогда – действительный нормальный вид отрицательно определенной квадратичной формы .

В матрице отрицательно определённой квадратичной формы, как нетрудно видеть, знаки главных миноров чередуются.

Глава 2. Евклидовы пространства §1. Скалярное произведение

Рассматриваем только действительные линейные пространства. В них можно ввести скалярное произведение векторов, обобщающее это понятие, известное для векторов-отрезков.

Определение 1. Пусть V – линейное пространство над полем R действительных чисел. Будем говорить, что на нем задано скалярное произведение, если на V определена симметрическая билинейная форма, обозначаемая (x,y), для которой соответствующая квадратичная форма (х,х) положительно определена.

Примеры. 1. Рассмотрим пространство R₃ векторов-отрезков. Если в некотором базисе заданы векторы х (х₁, х₂, х₃) и у (у₁, у₂, у₃), то полагаем (х, у) = х₁ у₁ + х₂у₂ + х₃у_3.

Легко проверить, что эта форма (у, х) = (х, у) – билинейная, а (х,х) = х₁² + х₂² + х₃² – положительно определенная квадратичная форма.

Значит, (х,у) – скалярное произведение в R₃ .

2. Пусть F – пространство непрерывных на [a, b] функций действительной переменной. Полагаем, что для любых функций φ(х) и ψ(х)  F скалярное произведение задается так: (φ(х), ψ(х)) = φ(х)ψ(х)dx.

Очевидно, это – симметрическая билинейная форма и, так как φ²(х)dx>0 при φ(х) ≠ 0, то (φ(х), φ(х))>0, то есть (φ(х), φ(х)) – положительно определенная квадратичная форма.

Учитывая определения симметричной билинейной и квадратичной форм, данное выше определение 1 скалярного произведения можно переформулировать следующим образом.

Определение 2. Пусть V – действительное линейное пространство. Будем говорить, что в V определено скалярное произведение, если по некоторому закону любой упорядоченной паре векторов a, b  V ставится в соответствие единственное действительное число (a,b) и выполняются следующие аксиомы скалярного произведения (для любых a, b, с V и любого R):

1) коммутативность (a,b) = (b,а);

2) (a+b, c)=(a,c)+(b,c);

3) (a,b)=  (a,b);

4) (a,a)>0 при любом а 0.

Определение 3. Действительное линейное пространство, на котором определено скалярное произведение, называется евклидовым пространством.

Замечание 1. Отметим, что скалярное произведение не является алгебраической операцией в V, так как a, b  V, но (a,b), вообще говоря, не принадлежит V (ибо поле не обязано содержаться в ).

Теорема (о превращении конечномерного линейного пространства в евклидово пространство). Во всяком конечномерном линейном пространстве V_n над R можно задать скалярное произведение, т.е. превратить его в евклидово пространство.

Доказательство. Выберем в V_n некоторый базис е₁, …, е_n. Пусть a, b  V_n. Тогда а = ₁е₁+…+_nе_n, b = ₁е₁+…+_nе_n.

По определению полагаем: (1). Нетрудно проверить, что выполняются все аксиомы скалярного произведения. В частности, при любом а0. Значит, V_n стало евклидовым пространством.

Теорема доказана.

Замечание 2. В связи с этой теоремой возникает ряд вопросов:

1. Если в V_n задавать скалярное произведение, как в теореме 1, но использовать различные базисы, то получим различные евклидовы пространства или у них есть что-то общее? Ответ на этот вопрос мы получим после введения понятия изоморфизма евклидовых пространств.

2. Можно ли в конечномерном линейном пространстве задать скалярное произведение принципиально другим способом? В дальнейшем будет доказано, что любой способ сводится к данному.