§ 4. Основная теорема о линейной зависимости. Ее следствия

Определение 4. Пусть даны две конечные системы векторов линейного пространства L:a₁,a₂,…,a_l (1) и b₁,b₂,…,b_s (2).

Если каждый вектор системы (1) линейно выражается через (2), то будем говорить, что система (1) линейно выражается через (2).

Примеры:

1. Любая подсистема системы a₁,…,a_i,…,a_k линейно выражается через всю систему, т.к. a_i=0a₁+…+1a_i+…+0a_k.

2. Любая система векторов-отрезков из R₂ линейно выражается через систему, состоящую из двух неколлинеарных векторов плоскости.

Определение 5. Если две конечные системы векторов линейно выражаются друг через друга, то они называются эквивалентными.

Замечание 1. Число векторов в двух эквивалентных системах может быть разным, что видно из следующих примеров.

Примеры:

3. Каждая система эквивалентна своему базису (это следует из теоремы 3 и примера 1).

4. Любые две системы векторов-отрезков из R₂, в каждой из которых есть два неколлинеарных вектора, эквивалентны.

Следующая теорема является одним из важнейших утверждений теории линейных пространств.

Основная теорема о линейной зависимости. Пусть в линейном пространстве L над полем P заданы две системы векторов:

a₁,a₂,…,a_l (1) и b₁,b₂,…,b_s (2), причем (1) линейно независима и линейно выражается через (2). Тогда ls (3).

Доказательство. Нам надо доказать неравенство (3). Предположим противное, пусть l>s (4).

По условию каждый вектор a_i из (1) линейно выражается через систему (2):

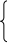a₁=α₁₁b₁+α₁₂b₂+…+α_1sb_s

a₂=α₂₁b₁+a₂₂b₂+…+α_2sb_s

…………………... (5)

a_l=α_l1b₁+α_l2b₂+…+α_lsb_s.

Составим следующее уравнение: x₁a₁+x₂a₂+…+x₁a_l=0 (6), где x_i— неизвестные, принимающие значения из поля Р (i=1,…,s).

Умножим каждое из равенств (5), соответственно на x₁,x₂,…,x_l, подставим в (6) и соберем вместе слагаемые, содержащие b₁, затем b₂ и, наконец, b_s. Получим:

x₁a₁+…+x_la_l = (α₁₁x₁+α₂₁x₂+ … +α_l1x_l)b₁ + (α₁₂x₁+α₂₂x₂+ … +α_l2x_l)b₂ + …+(α_1sx₁+α_2sx₂+…+α_lsx_l)b_s=0. (7)

Постараемся найти ненулевое решение уравнения (6). Для этого приравняем в (7) к нулю все коэффициенты при b_i (i=1, 2,…,s) и составим следующую систему уравнений:

α₁₁x₁+α₂₁x₂+ … +α_l1x_l=0

α₁₂x₁+α₂₂x₂+…+α_l2x_l=0 (8)

…………………….

α_1sx₁+α_2sx₂+…+α_lsx_l=0.

(8)  однородная система s уравнений относительно неизвестных x₁,…,x_l. Она всегда совместна.

В силу неравенства (4) в этой системе число неизвестных больше числа уравнений, и потому, как следует из метода Гаусса, она приводится к трапецеидальному виду. Значит, существуют ненулевые решения системы (8). Обозначим одно из них через x₁⁰,x₂⁰,…,x_l⁰ (9), x_i⁰P (i=1, 2,…s).

Подставив числа (9) в левую часть (7), получим:

x₁⁰a₁+x₂⁰a₂+…+x_l⁰a_l=0b₁+0b₂+…+0b_s=0. (10)

Итак, (9) – ненулевое решение уравнения (6). Поэтому система (1) линейно зависима, а это противоречит условию. Следовательно, наше предположение (4) неверно и ls.

Теорема доказана.