§2. Алгебраическая форма комплексного числа

Пусть α=(a,b) С. Тогда α=(a,b)=(a,0)+(0,b)=(a,0)+(b,0)∙(0,1)=a+bi.

Определение . Форма α=a+bi (где a,b – действительные числа) называется алгебраической формой комплексного числа.

Число i называется мнимой единицей, а – действительной частью числа α, bi – мнимой частью числа α. Числа вида bi называются мнимыми числами.

Отметим, что комплексные числа – это объединение действительных и недействительных чисел (но не действительных и мнимых!).

Теперь из определений операций (2) и (3) нетрудно установить правила действия над комплексными числами в алгебраической форме:

(a+bi)±(c+di)=(a±c)+(b±d)i,

(a+bi)∙(c+di)=(ac-bd)+(ad+bc)i,

Замечание. Если плоскость рассматривается как система комплексных чисел, то обычно координатные оси обозначаются так: R – действительная ось (бывшая ось ОХ), I – мнимая ось (бывшая ось ОY).

Геометрическая интерпретация сложения и вычитания комплексных чисел.

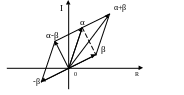
Рис.1

§3. Тригонометрическая форма комплексного числа

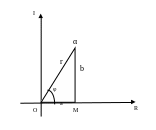
α=a+bi

Рис.2

Определение 1. Число r =|0α|≥0 называется модулем числа α, а угол φ – аргументом α (φ отсчитывается от положительного направления оси R против часовой стрелки).

Аргументов у каждого числа α бесконечно много, их общий вид φ+2πk(kЄZ). У любого комплексного числа, отличного от нуля, существует аргумент. Любое число α≠0 однозначно характеризуется модулем r и каким-либо аргументом φ; эти характеристики обычно называются полярными координатами точки α .

Из рисунка 2 видно, что a=rcos φ, b=rsin φ; тогда α=a+bi=r(cosφ+isinφ).

Определение 2. Форма α=r(cosφ+isinφ) называется тригонометрической формой комплексного числа.

Числа r и φ находят так: , .

Отметим, что если известен tg φ и известно, в какой четверти находится точка α, то однозначно находится угол φ (меньший 2π).

Замечание 1. Аргумент числа α можно отсчитывать и по часовой стрелке, но брать со знаком « - ».

В тригонометрической форме удобно умножать и делить комплексные числа. Нетрудно проверить, используя формулы синуса и косинуса суммы и разности двух углов (см., например, [1]), что справедливы следующие правила: если α=r(cosφ+isinφ) и β=r₁(cosφ₁+isinφ₁), то αβ=rr₁(cos(φ+φ₁)+isin(φ+φ₁)), (5)

и при β0

(6)

Из (5) и (6) получаем:

, ,

, при β0.

Замечание 2. Из рис. 1 видно, что - равен расстоянию между точками α и β (это  геометрический смысл модуля разности). Из этого рисунка, рассмотрев треугольники О(+) и О (и некоторые простые частные случаи), получаем

-++. Геометрическая интерпретация умножения – на рис. 3. Аналогичным образом, заменяя через β^-1, можно получить геометрическую интерпретацию деления.

Рис.3