§5. Подполя и расширения полей
Определение
1. Пусть Р –
некоторое поле. Подмножество
называется
подполем
поля Р, если
S
само является полем относительно тех
же операций, что и Р. В этом случае Р
называется расширением
поля S.
Из
определения подполя видно, что для того,
чтобы S
было подполем поля Р достаточно
выполнения следующих условий для любых
:
1.
;
2.
;
3.
;
4.
при
.
Остальные аксиомы поля для S проверять не нужно, т.к. они выполняются для любых элементов из поля Р.
Примеры.
Q – поле рациональных чисел является подполем поля комплексных чисел С; С – расширение поля Q.
Легко доказывается следующая
Теорема 3. Пересечение любого множества подполей поля Р также является подполем поля Р.
Определение
2. Пусть S
– некоторое подполе поля Р и
.
Обозначим через
пересечение всех подполей Pd
поля Р, таких, что
и
.
Подполе S(a)
называется расширением
поля S,
полученным путем присоединения к нему
элемента а.
Отметим, что подполе S(a) существует ввиду теоремы 3. Нетрудно видеть, что S(a) – минимальное расширение поля S, содержащее элемент а.
§6. Изоморфизм колец (полей)
Определение.
Пусть K
и K’
два кольца (поля). Они называются
изоморфными
(
),
если существует биективное отображение
такое, что
Само такое отображение φ называется изоморфным отображением или изоморфизмом.
С точки зрения алгебры изоморфные алгебраические структуры считаются одинаковыми и всегда можно заменять алгебраические структуры на изоморфные им.
Пример.
Рассмотрим поле R
и поле S
всех точек оси ОХ. Зададим отображение
φ так:
.
Нетрудно видеть, что φ – изоморфизм R
и S,
т.е.
.
Это объясняет привычную для нас еще со
школы замену действительных чисел
точками оси ОХ.
§7. Построение поля комплексных чисел на языке подполей и расширений
Проведенное в §1 главы I построение поля С содержало ряд нестрогостей. Сейчас мы их устраним на языке подполей и расширений.
Задача,
которую мы ставили при построении
комплексных чисел, теперь ставится так:
найти расширение поля R
с помощью корня уравнения
.
Если через i обозначить какой-то корень этого уравнения, то нам нужно найти R(i) – минимальное расширение поля R,
содержащее i.
Решение этой задачи проводим по следующим этапам:
Рассмотрим множество С всех точек плоскости XOY. В этом множестве вводим операции сложения, умножения (как в §1 гл.I). Проверяем, что С – поле (выполнение большинства аксиом поля в С в §1 гл.1 проверялось).
Во множестве С рассматриваем подмножество
,
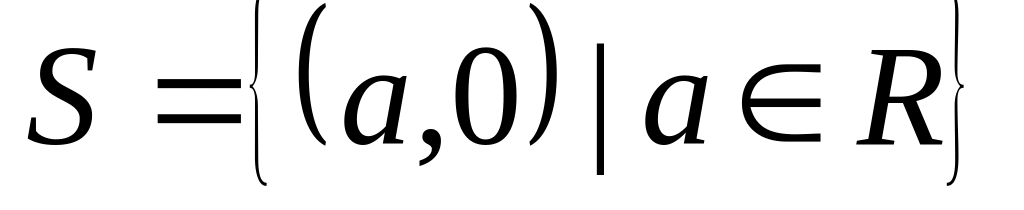состоящее из всех точек оси ОХ. Проверяем,
что S
– подполе поля С.
Для
этого достаточно убедиться в следующем:
,
.
Рассмотрим отображение
,
т.е.
.
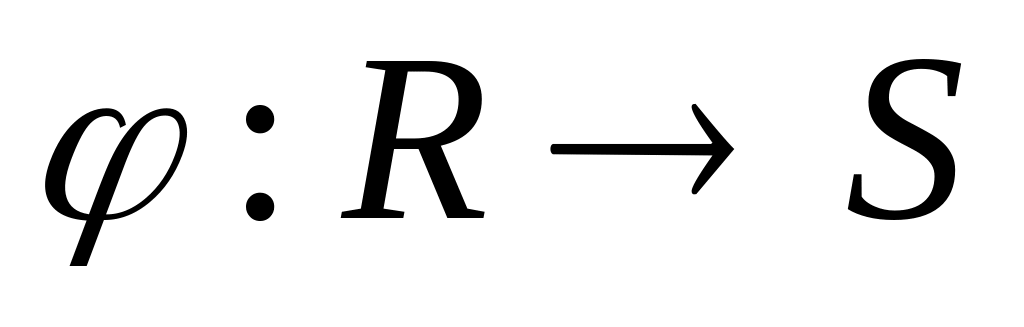Проверяем, что φ – изоморфизм полей R
и S
(это нетрудно), т.е.
.
На основании этого изоморфизма
отождествляем точки оси ОХ и действительные
числа, т.е. полагаем:
.
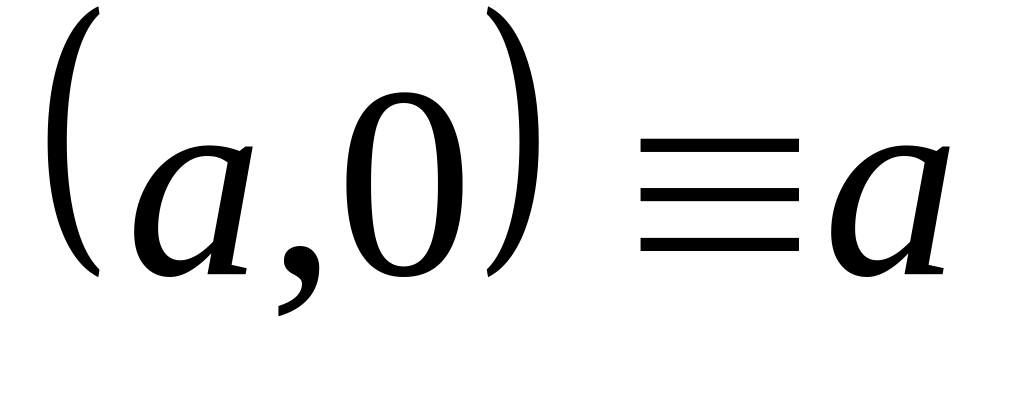Получаем, что
;
следовательно, С – расширение поля R.
Рассмотрим точку
,
и проверяем, что
(в §1 гл.1 это сделано). Как и в §1 гл.1,
получаем алгебраическую форму комплексных
чисел, т.е.
.
Проверим, что R(i)=C.
Т.к.
и
R(i)
поле, то из
для любых
имеем:
,т.к.
;
.
А тогда
.
Следовательно,
;
но
;
значит,
.
Поставленная задача решена.