Единственность единичной и обратной матриц

Пусть Е – единичная матрица n-го порядка и Е₁ – другая единичная матрица того же порядка. По определению единичной матрицы имеем: для любой матрицы А n-го порядка выполняются равенства:

,

.

Докажем, что Е=Е₁. Рассмотрим произведение EE₁.

Имеем: , т.к. Е₁ – единичная матрица; с другой стороны, , т.е. Е – единичная матрица. Следовательно, Е=Е₁.

Пусть А – любая невырожденная матрица n-го порядка. Докажем, что она имеет ровно одну обратную матрицу.

Как показано выше, хотя бы одна обратная к A матрица А^-1 существует.

Пусть В – тоже обратная матрица к А, т.е. , .

Рассмотрим произведение А^-1АВ. С одной стороны, в силу ассоциативности умножения матриц, ; с другой стороны, . Следовательно, А^-1=В.

Мы доказали

Утверждение 2. У каждой невырожденной матрицы существует ровно одна обратная матрица.

§5. Решение матричных уравнений

Определение 1. Прямоугольные матрицы С и D будем умножать по тому же правилу, что и квадратные, если число столбцов матрицы С равно числу строк матрицы D (чтобы строку первой матрицы можно было умножить на столбец второй матрицы по старому правилу).

Можно проверить, как и для квадратных матриц, что умножение прямоугольных матриц ассоциативно, т.е. если матрицы (АВ)С и А(ВС) существуют, то они равны.

Рассмотрим уравнение вида АХ=В (1), где А и В – данные матрицы (вообще говоря, прямоугольные), Х – неизвестная матрица.

Пользуясь ассоциативностью умножения прямоугольных матриц, мы можем решать матричные уравнения (1) для некоторых «хороших» матриц А.

1. Если в уравнении (1) матрицы А и В произвольные, то это уравнение сводится к системе линейных уравнений, если число строк s матрицы А равно числу строк k матрицы В, т.е. s=k (2). Если равенство (2) не выполняется, то уравнение (1) не имеет решения.

2. Пусть А – невырожденная квадратная матрица n-го порядка и матрица В имеет n строк.

Предположим, что уравнение (1) имеет хотя бы одно решение, т.е. существует матрица Х₀ такая, что АХ₀=В (3).

По условию для А существует обратная матрица А^-1. Умножая обе части равенства (3) слева на матрицу А^-1, получим:

(4). В силу ассоциативности умножения имеем: (5). Из равенств (4) и (5) следует: . (6)

Мы доказали что, если уравнение (1) имеет решение, то любое решение имеет вид (6), и потому решение единственно (ввиду единственности обратной матрицы).

Для доказательства существования решения подставим в левую часть уравнения (1) вместо Х произведение А^-1В. Имеем: .

Доказано

Утверждение. Матричное уравнение (1) с невырожденной матрицей А, в котором число строк матрицы В равно порядку матрицы А, имеет единственное решение X=A^-1B.

Матричное доказательство теоремы Крамера

Рассмотрим систему n линейных уравнений с n неизвестными с комплексными коэффициентами:

, (7)

где .

Рассмотрим следующие матрицы: матрицу А системы (7):

, , .

Нетрудно видеть, что система (7) в матричном виде запишется следующим образом: АХ=В. (8)

Как доказано выше, уравнение (8) для случая, когда , имеет единственное решение . (9)

Пусть .

Учитывая вид обратной матрицы, полученный ранее, равенство (9) перепишем в виде:

.

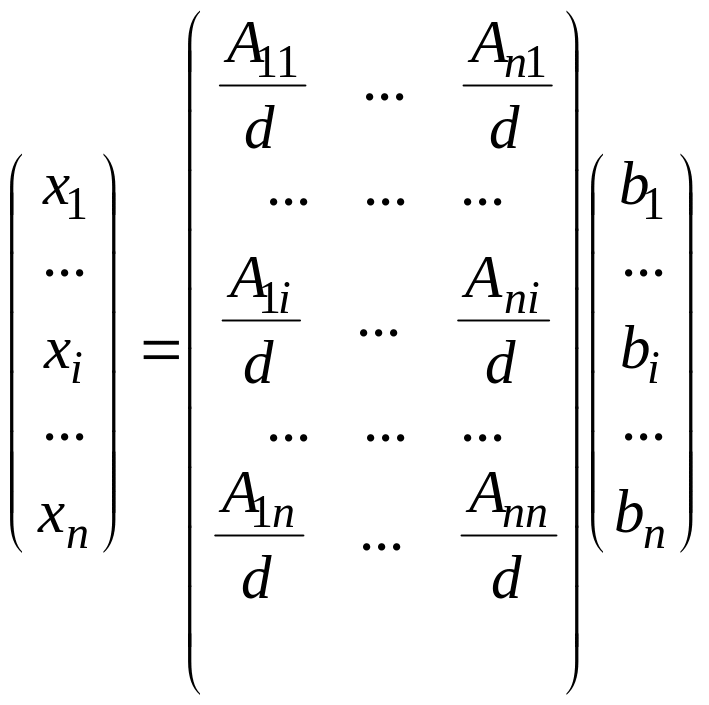Следовательно, , где

.

Мы доказали следующую теорему:

Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой , имеет единственное решение:

,

где d_i – определитель, полученный из определителя системы d путем замены i-го столбца столбцом свободных членов, .

Замечание. Напомним, что решением системы с n неизвестными называется упорядоченный набор n чисел, при подстановке которых вместо соответствующих неизвестных каждое уравнение этой системы обращается в тождество.

Определение 2. Система линейных уравнений (7), у которой , называется однородной.

Однородная система всегда совместна, т.к. всегда имеет нулевое решение. Отличные от него решения однородной системы, если они существуют, называются ненулевыми.

Из теоремы Крамера легко вытекают следующие утверждения:

Следствие 1. Если для однородной системы n уравнений с n неизвестными ее определитель отличен от нуля, то она имеет только нулевое решение.

Следствие 2. Если однородная система n уравнений с n неизвестными имеет ненулевое решение, то ее определитель равен нулю.