§3. Вычисление определителей

Определение 1. Пусть d – определитель n-го порядка (с комплексными элементами). Определители порядков 1, 2, …, n, “cодержащиеся” в d, называются минорами определителя d.

Пусть минор М k-го порядка определителя d расположен на пересечениях строк с номерами i₁, i₂, ..., i_k и столбцов с номерами j₁, j₂, ..., j_k этого определителя.

Введем обозначение: S_M=( i₁+i₂+ ...+i_k )+( j₁+j₂+...+j_k).

Определение 2. Определитель M’, который получается из определителя d путем вычеркивания всех строк и столбцов, в которых расположен минор М, называется дополнительным минором к минору М в d.

Отметим, что М и М’ – взаимно дополнительные миноры.

Замечание 1. Дополнительный минор есть не у каждого минора: например, у минора n-го порядка нет дополнительного.

Определение 3. Алгебраическим дополнением А минора М определителя d в d называется минор M’, умноженный на , т.е. .

Обычно используют следующие обозначения: если a_ij – элемент определителя d, то через M_ij обозначает дополнительный минор этого элемента (как минора первого порядка) в определителе d, а A_ij – алгебраическое дополнение элемента a_ij в d, т.е. .

Вычисление определителя n-го порядка можно свести к вычислению одного или нескольких определителей (n-1)-го порядка. Сначала научимся вычислять определители, у которых в одной строке все элементы, кроме одного, отличны от нуля.

Лемма 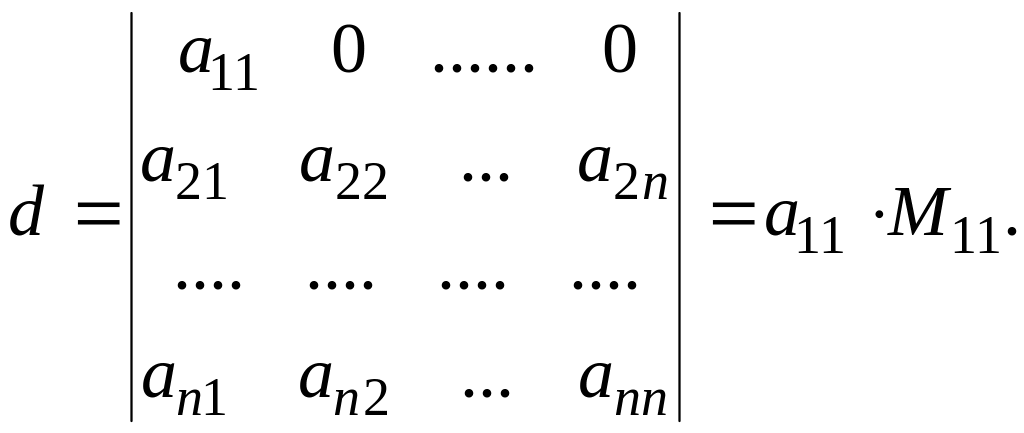1.

(11)

Доказательство. Если а₁₁=0, то d=0.Пусть а₁₁0. Рассмотрим произвольный ненулевой член определителя d. В силу условия леммы из первой строки в него войдет элемент a₁₁. Поэтому все такие члены имеют вид (12), (13), . Знак члена (12) в определителе d определяется подстановкой (14). Таким образом, d – алгебраическая сумма членов (12) со знаками, определяемыми подстановкой (14).

Если в этой сумме вынести за скобки множитель a₁₁, то получим: (15), где S – алгебраическая сумма всевозможных членов вида (16) со знаками, определяемыми подстановками (14). Нетрудно видеть, что (16) – это все члены минора M₁₁ . Знак члена (16) в M₁₁ определяется подстановкой (17) (на самом деле здесь все числа должны быть на единицу меньше, но на четность подстановки это не влияет). Подстановка (17) имеет, очевидно, ту же четность, что и подстановка (14) (т.к. число 1 в нижней строке подстановки (14) не составляет инверсий).

Итак, S – алгебраическая сумма всевозможных членов минора M₁₁ с их знаками, т.е. S=M₁₁. Отсюда из равенства (15) получаем: (18). Лемма доказана.

Лемма 2.

(19)

Доказательство. Для доказательства определитель d с помощью перестановок строк и столбцов преобразуем так, чтобы элемент a_ij перешел в левый верхний угол, но при этом не изменился дополнительный минор M_ij к элементу a_ij. Для этого i-ую строку определителя d поменяем местами с предыдущей, затем опять с предыдущей и т.д., пока она не займет место первой строки. Заметим, что каждый раз, когда мы меняем местами строки, меняется знак определителя. Получим следующий определитель:

.

Очевидно, (20) и d₁ получается из d путем

(i-1) перестановок строк. Точно также в определителе d₁ c помощью (j-1) перестановок столбцов переводим элемент a_ij в левый верхний угол.

и . (21)

Подставляя d₁ из (20) в (21), получим: . Следовательно, . (22)

В силу леммы 1, примененной к определителю d₂, получаем: (23) (мы использовали то, что в определителе d₂ дополнительным минором к элементу a_ij, будет тот же самый минор, который был дополнительным к a_ij в d, т.е. M_ij ).

Из равенств (22) и (23) следует: .

Лемма доказана.

Теперь мы можем получить правило вычисления любого определителя n-го порядка.

Теорема 5 (разложение определителя по строке). Определитель d равен сумме произведений элементов какой-либо его строки на их алгебраические дополнения в d, т.е.

(24)

Доказательство. Рассмотрим в определителе d произвольную i-ую строку. Каждый элемент этой строки представим в виде суммы самого этого элемента и (n-1) нулей следующим образом:

,

,

…,

По свойству 5 определитель d тогда можно представить в виде суммы определителей:

Теперь, применяя лемму 2 к каждому из определителей, стоящих справа, и учитывая тот факт, что при нахождении алгебраических дополнений элементов i-ой строки элементы самой этой строки вычеркиваются, т.е. могут быть любыми, мы получим:

.

Теорема доказана.

Некоторые определители (например, содержащие «большие» миноры из нулей) удобнее вычислять с помощью разложения по нескольким строкам, сводящего вычисление определителя n-го порядка к вычислению определителей k-го и (n-k)-го порядков.

Теорема Лапласа. Пусть в определителе n-го порядка d выделены какие-либо k строк (или k столбцов), где . Тогда сумма произведений всех миноров k-го порядка определителя d, содержащихся в этих строках, на их алгебраические дополнения равна самому определителю d.

Доказательство этой теоремы мы не приводим.

Замечание 2. Пусть M₁, M₂, ..., M_s – все миноры k-го порядка в рассматриваемых строках определителя и, соответственно, А₁, А₂, ..., А_s – их алгебраические дополнения в d. Тогда теорема утверждает, что

.