6.2. Проверка первой, второй предпосылок мнк

Проверка первой предпосылки

Для проверки случайного характера остатков строится график зависимости остатков е, от теоретических значений результативного признака

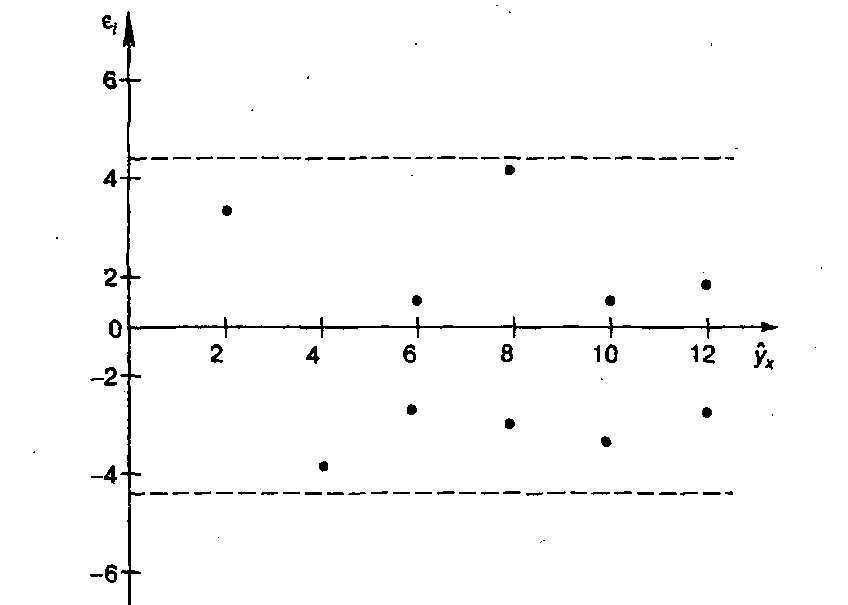
Зависимость случайных остатков е_i, от теоретических значений

Если на графике получена горизонтальная полоса, то остатки е, представляют собой случайные величины и расчетные значения У_р хорошо аппросимируют фактические значения У.

Проверка второй предпосылка

Вторая предпосылка имеет две составляющих:

- среднее значение остатков должно равняться нулю или сумма остатков модели должна равняться нулю;

- остатки не должны зависеть от значений Х_i.

Если коэффициенты определены МНК, то сумма остатков равняется нулю Σе_i = 0 выполняется для линейных моделей и моделей.

Для проверки независимости остатков е_i от значений Х_i строится график зависимости остатков е_i от Х_i

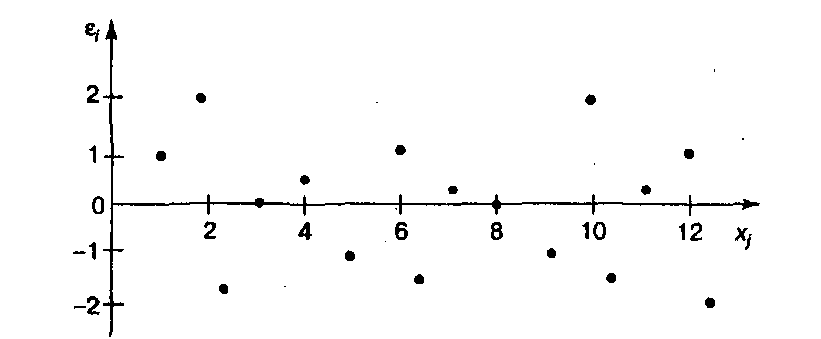
Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений Xj.

Если же график показывает наличие зависимости е_i и Xj, то имеется возможность улучшить модель с помощью выбора другой математической функции.

6.3. Проверка третьей, четвертой предпосылок мнк

Проверка третьей предпосылки.

В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной (однородной, одинаковой).

Это значит, что для каждого значения фактора Xj остатки е, имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность (неоднородность, разный).

Наличие гетероскедастичности можно наглядно видеть на полях корреляции

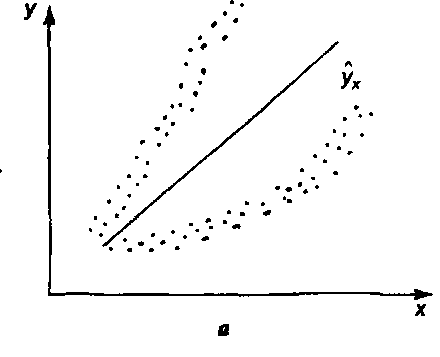
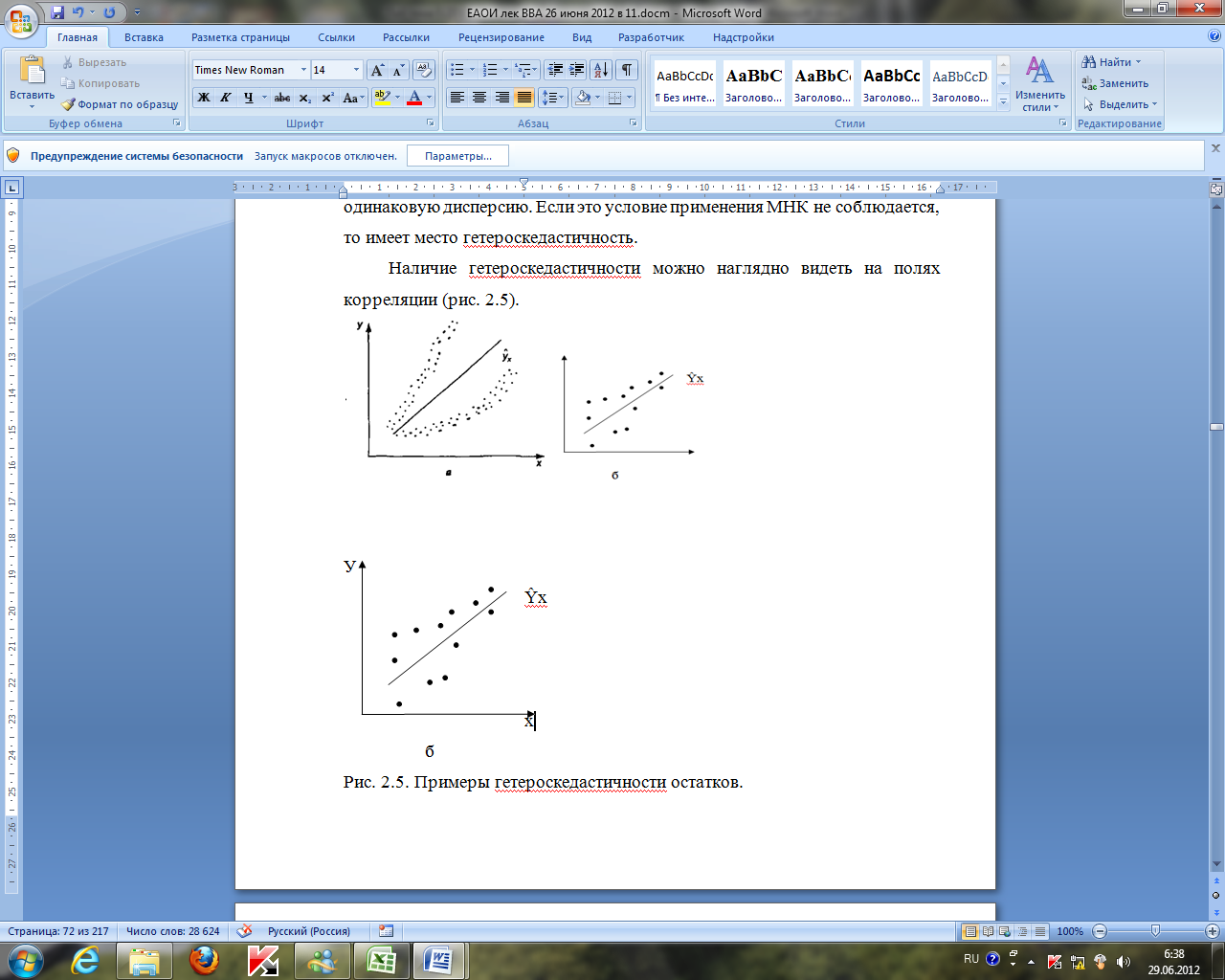
На рис. а остатки являются не однородными (разными), дисперсия остатков растет по мере увеличения Х

На рис. б – дисперсия остатков уменьшается в зависимости от Х.

Причинами появления гетероскедастичности остатков являются:

• плохая спецификация модели,

• наличие в базе данных двух и более групп объектов, свойства которых сильно отличаются между собой.

Последствия гетероскедастичности:

• уравнение регрессии может описывать свойства тех объектов, которых вообще нет,

• доверительные интервалы регрессии и прогноза не соответствуют фактическим значениям остатков.

В тест Голдфелда-Квандта используется критерий Фишера, который выполняется в следующем порядке:

1. Все n наблюдений упорядочиваем по величине X.

2. После этого всю упорядоченную выборку разбиваем на три равные подвыборки размерностью n.

3. Оцениваем отдельные регрессии для первой подвыборки (n первых наблюдений) и для третьей подвыборки (n последних наблюдений).

4. Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия остатков по n первой подвыборке будет существенно меньше дисперсии остатков по n третьей подвыборке.

5. Выдвигается нулевая гипотеза: H₀: S₃^{2 =} S₁² о равенстве дисперсий или об отсутствии гетероскедастичности.

6. Для проверки нулевой гипотезы используется критерий Фишера - F-статистику:

F_набл = S₃² / S₁² ,

где S₃² и S₁² - дисперсии остатков для третьей и первой совокупности

,

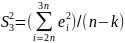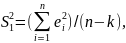
n-k - число степеней свободы выборочных дисперсий остатков;

n – объем выборки;

k — количество коэффициентов в уравнении регрессии, включая свободный коэффициент.

При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы ν₁ = n-k; ν₂ = n-k.

7. Если F_набл = S₃²/S₁² >F_крит = F_α,v1,v2;, то нулевая гипотеза H₀: S₃^{2 =} S₁² об отсутствии гетероскедастичности, отклоняется на уровне значимости α. В противном случае нулевая гипотеза H₀: S₃^{2 =} S₁² об отсутствии гетероскедастичности принимается и утверждается, что остатки являются гомоскедастичными, но не указывается с какой вероятностью.

Проверка четвертой предпосылки

Четвертая предпосылка МНК предполагает отсутствие автокорреляции остатков или отсутствие связи остатков между собой.

Автокорреляция остатков порядка m равна коэффициенту корреляции, рассчитанному между исходными остатками модели и лаговыми остатками порядка m.

Пояснения к введенным понятиям.

Лаг

Лаг – задержка. Например, временной лаг (задержка) между причиной и следствием.

Лаговые остатки порядка m.

Для модели У_t = a₀+a₁t+e_t временного ряда У_t, можно рассчитать коэффициенты и а₀, а₁ и остатки модели е_t.

Остатки модели представим в виде таблицы

t	et	et-1
1	E1
2	E2	E2-1=e1
3	E3	E3-1=e2
4		E4-1=e3

Если остатки временного ряда сместить на одну дату, то получатся е_t-1 лаговые остатки первого порядка

Если остатки временного ряда сместить на две даты, то получатся е_t-2 лаговые остатки второго порядка