20.3.Модели стационарных временных рядов

Если временной ряд стационарен, то это означает, что численные значения временного ряда изменяются около среднего значения с примерно одинаковой амплитудой без четко выраженных периодических колебаний.

Стационарные временные ряды могут получаться после моделирования нестационарного временного ряда, остатки которого являются стационарными.

К основным линейным моделям стационарных временных рядов относятся:

1) Модели авторегрессии;

2) Модели скользящего среднего;

3) Модели авторегрессии и скользящего среднего.

Модели авторегрессии

Уровень временного ряда, представленного моделью авторегрессии порядка р, можно представить следующим образом:

У_t=δ₁У_t-1+δ₂У_t-2+…+δ_pУ_t–p+ν_t,

где p – порядок модели авторегрессии;

δt – коэффициенты модели авторегрессии, подлежащие оцениванию;

νt – белый шум (случайная величина с нулевым математическим ожиданием).

Модель авторегрессии порядка р обозначается как АР(р) или AR(p).

На практике чаще всего используются модели авторегрессии первого, второго, ма имум третьего порядков.

Модель авторегрессии первого порядка АР(1) называется «Марковским процессом», потому что значения переменной У в текущий момент времени t зависят только от значений переменной У в предыдущий момент времени (t–1). Данная модель имеет вид:

У_t=δУ_t–1+ν_t.

Модель авторегрессии второго порядка АР(2) называется «процессом Юла». Данная модель имеет вид:

У_t=δ₁У_t-1+δ₂У_t-2+νt.

Модели скользящего среднего

Модели скользящего среднего относятся к простому классу моделей временных рядов с конечным числом параметров, которые можно получить, представив уровень временного ряда как алгебраическую сумму членов ряда белого шума с числом слагаемых q.

Общая модель скользящего среднего порядка q имеет вид:

У_t=ν_t–φ₁ν_t–1–φ₂ν_t–2–…–φ_qν_t–q,

где q – порядок модели скользящего среднего;

φ_t – неизвестные коэффициенты модели, подлежащие оцениванию;

ν_t – белый шум.

Модель скользящего среднего порядка q обозначается как CC(q) или MA(q).

Модели авторегрессии и скользящего среднего

Для достижения большей гибкости модели временных рядов при эконометрическом моделировании в неё включают как члены авторегрессии, так и члены скользящего среднего. Подобные модели получили название смешанных моделей авторегрессии и скользящего среднего и также относятся к линейным моделям стационарных временных рядов.

Смешанная модель авторегрессии и скользящего среднего обозначается как АРСС(p,q) или ARMA(p,q).

Чаще всего на практике используется смешанная модель АРСС(1) с одним параметром авторегрессии p=1 и одним параметром скользящего среднего q=1. Данная модель имеет вид:

У_t=δУ_t–1+ν_t–φν_t–1,

где δ – параметр процесса авторегрессии;

φ – параметр процесса скользящего среднего;

ν_t – белый шум.

На коэффициенты данной модели накладываются следующие ограничения:

1) |δ|<1 – условие, обеспечивающее стационарность смешанной модели;

2) |Φ|‹1 – условие, обеспечивающее обратимость смешанной модели.

20.4. Модели нестационарных временных рядов

Если временной ряд нестационарен, то это означает, что временной ряд содержит или линейную тенденцию или гетероскедастичность остатков или автокорреляцию остатков или периодическую составляющую или все вместе.

Рассмотрим следующие модели нестационарных временных рядов.

Модель периодических составляющих временных рядов.

Модель гетероскедастичности временных рядов.

Модель автокорреляции остатков.

Модель периодических составляющих временных рядов

Представим временной ряд в виде аддитивной модели, имеющей следующие компоненты:

У_t = f_1t + f_2t + f_3t + e_t.

Моделирование тренда f_1t

Включение в модель У_t = f_1t + e_t тренда преследует две цели:

• первая – определить долговременную тенденцию временного ряда для получения долгосрочных прогнозов;

• вторая – преобразование нестационарного временного ряда в стационарный, для выделения в них периодических составляющих.

Тренд f_1t обычно воспроизводится с помощью следующих математических функций, которые слабо искажают периодические составляющие:

f_1t= a₀ + a₁*t,

f_1t= a₀ + a₁*lnt,

f_1t= a₀ + a₁/t.

Наибольшее распространение получила линейная функция, так как она не оказывает влияния на периодическую составляющую временного ряда.

Все остальные функции искажают периодическую составляющую временного ряда, поэтому не получили широкого применения.

Коэффициенты модели У_t = f1_t + e_t определяются методом наименьших квадратов.

Моделирование сезонной и циклических компонент (f_2t f_3t)

Сезонная и циклическая компоненты являются периодическими с разными периодами.

Обычно, в экономических временных рядах на длинно периодическую циклическую составляющую накладывается сезонная волна.

Можно предложить методику определения всех периодических составляющих временного ряда, в том числе сезонных и циклических, определить их достоверность и затем их включить в модель.

Процесс моделирования сезонной и циклической компонент выполняется в следующей последовательности.

Шаг 1. Выбор модели для выявления периодических составляющих.

Для выявления периодических составляющих временного ряда используется следующая модель:

У_t = a₀ + a₁*t + a₂*Sin(2t/T) + a₃*Cos(2t/T) + e_t,

где а₀, а₁, а₂, а₃ – коэффициенты, определяемые методом наименьших квадратов;

а₀ + а₁*t = f_t – линейная функция (тренд), которая приводит временной ряд к стационарному виду с нулевым средним значением, без искажения периодических составляющих остатка;

Sin(2t/T), Cos(2t/T) – тригонометрические функции периодической составляющей временного ряда, сумма которых позволяет учесть начальную фазу колебания;

t – порядковый номер времени;

Т – период или длина волны циклической составляющей временного ряда.

Длительность периода Т исследователь задает в интервалах от трех единиц до удвоенной длины временного ряда. Дальнейшее увеличение длины волны приводит к тому, что небольшие отрезки этой волны начинают описывать нециклические тенденции временного ряда;

(2t/T) - аргумент тригонометрической функции, выраженный в радианах;

1/Т – частота, численно равная количеству колебаний в единицу времени;

Шаг 2. Создается база данных.

Х₁ - t - время,

Х₂ - Sin(2t/T),

Х₃ - Cos(2t/T),

У - значения показателя временного ряда,

Т - период циклической составляющей, значение которого вводит иследователь в пределах от 3 до удвоенной длины временного ряда.

Шаг 3. Вычисление ошибки модели Е.

Вычисление Е ошибки модели

У_t = a₀ + a₁*t + a₂*Sin(2t/T) + a₃*Cos(2t/T) + e_t

с помощью статистической функции ЛИНЕЙН.

Переход к шагу 2 с изменением периода Т.

Шаг 4. Построение периодограммы - графика зависимости ошибки модели Е временного ряда от периода Т циклического фактора, включенного в модель.

Строится периодограмма - график зависимости Е от Т.

Шаг 5. Определение периодических составляющих временного ряда.

Определяются такие значения периодов Т, при которых ошибка модели имеет локальные минимумы. Обнаруженные периоды характеризуют периодические составляющие временного ряда, среди которых надо исключить ложные периоды. Ложная периодичность относится к периодам (эхам), которые являются кратными величине основного периода. Основной период имеет наименьшую ошибку модели, а кратные периоды или ложные периоды имеют большую ошибку модели. Например, квартальная периодическая составляющая (3 месяца) порождает эхо на периодах: 3*2=6 месяцев или полугодовой период, 3*3 =9 месяцев, 3*4 =12 месяцев или годовой период и т.д.

Шаг 6. Определение достоверных периодических составляющих временного ряда.

Для определения достоверных периодических составляющих необходимо построить модель с участием всех обнаруженных периодических составляющих и по критерию Стьюдента определить достоверность коэффициентов, стоящих перед тригонометрическими функциями, с использованием статистической функции ЛИНЕЙН Excel.

Для определения достоверности периодических составляющих строится модель вида:

У_t= a₀ + a₁*t + a₂*Sin(2t/T₁) + a₃*Cos(2t/T₁) + a₄*Sin(2t/T₂) + a₅*Cos(2t/T₂) + … + e_t,

где Т₁ и Т₂ - периоды выделенных периодических составляющих.

Анализ характеристик многофакторной модели производится обычным образом. Коэффициенты модели, достоверные по критерию Стьюдента укажут на достоверность наличия соответствующей периодической составляющей временного ряда.

Если периодических составляющих много, то можно автоматизировать процесс выделения достоверных периодических составляющих с помощью шагового метода включения с участием всех обнаруженных периодических составляющих. При этом возникают трудности, связанные с тем, что шаговый метод может включить в модель только одну составляющую периодической компоненты Sin(2t/T) или Cos (2t/T).

Шаг 7. Построение модели временного ряда.

Окончательная модель временного ряда с включением всех компонент может иметь следующий вид:

У_t= a₀ + a₁*t + a₂*Sin(2t/T1) + a₃*Cos(2t/T1) + a₄*Sin(2t/T2) + a₅*Cos(2t/T2) + e_t,

где a₀ + a₁t =f1_t - тренд,

a₂*Sin(2t/T1) + a₃*Cos(2t/T1) = f2_t – сезонная компонента,

Т1 = период сезонной компоненты,

a₄*Sin(2t/T2) + a₅*Cos(2t/T2) = f3_t – циклическая компонента,

Т2 – период циклической компоненты,

е_t – остатки модели.

Коэффициенты модели рассчитываются методом наименьших квадратов.

Многолетний опыт применения изложенной методики моделирования временных рядов для различных экономических переменных позволяет судить о ее высокой эффективности.

Однако существуют следующие проблемы предложенной модели временного ряда:

• обнаруженные периодические составляющие временного ряда должны иметь экономическое обоснование и механизм их возникновения;

• для построения доверительных интервалов регрессии и прогноза необходимо считать более точным не среднее значение временного интервала, а его последнее более свежее значение.

Модель гетероскедастичности временных рядов

Произведем моделирование гетероскедастичности временных рядов.

Временной ряд является нестационарным, если дисперсии временного ряда не одинаковы на разных его участках.

На рис. показан временной ряд, который является нестационарным по среднему значению с гомоскедастичными остатками

Гомоскедастичность остатков - однородность остатков.

Однородность переменной У - свойство переменной У, которое заключается в том, что дисперсии переменной У для каждого фи ированного значения Х являются постоянными.

Гетероскедастичность остатков- неоднородность остатков, дисперсии остатков для каждого фи ированного значения Х достоверно отличаются между собой.

Гетероскедастичность - неоднородность численных значений переменной У.

Причины появления гетероскедастичности остатков:

• плохая спецификация модели,

• наличие в базе данных двух и более групп объектов, свойства которых сильно отличаются между собой.

Последствия гетероскедастичности:

• уравнение регрессии может описывать свойства тех объектов, которых вообще нет;

• доверительные интервалы регрессии и прогноза не соответствуют фактическим значениям остатков.

Критерии проверки достоверности гетероскедастичности.

Для обнаружения гетероскедастичности используется:

- визуальный метод.

Для проверки достоверности гетероскедастичности используется:

- критерий Гольдфельда-Квандтома.

Критерий Гольдфельда-Квандтома использует критерий Фишера анализа двух дисперсий остатков, определенных для двух групп остатков, взятых определенным образом из совокупности всех остатков.

Методы устранения гетероскедастичности остатков.

Известно несколько методов устранения гетероскедастичности остатков:

- метод выделения однородных объектов,

- обобщенный метод наименьших квадратов или метод Эйткена.

Метод выделения однородных объектов.

Самый простой метод это выделение группировка однородных объектов, для которых остатки модели будут однородными.

Обобщенный метод наименьших квадратов или метод Эйткена.

Линейное регрессионное уравнение имеет следующий вид:

У_i = a₀ + a₁*X_I + e_i.

Если все уравнение разделить на модуль остатков e_i, то для новых переменныхостатки новой модели будут принимать значения 1 или -1.

Следовательно, остатки новой модели будут гомоскедастичны.

Однако, возникают трудности в экономической интерпретации новых переменных.

Коэффициенты модели, определенные по преобразованным данным называются коэффициентами обобщенного метода наименьших квадратов или коэффициентами Эйткена.

Коэффициенты Эйткена обладают следующими свойствами:

- если коэффициенты Эйткена использовать для не преобразованных данных, то уравнение регрессии пройдет ближе к тем значениям, которые имеют меньшие остатки;

- если произвести полный эконометрический анализ для преобразованных данных, а затем полученные точечный, доверительные интервалы для прогноза и уравнения регрессии умножить на модуль остатков e_i, то новые точечный и интервальный прогноз и доверительные интервалы уравнения регрессии будут учитывать свойства остатков для фактических не преобразованных значений зависимой переменной.

Модель автокорреляции остатков

Если из временного ряда исключить линейную тенденцию

У_t –(а₀ +а₁*Х_t) = e_t,

то остатки модели e_t, могут иметь следующие закономерности их поведения:

- быстро изменяться около среднего значения остатков, равных нулю;

- плавно изменяться по периодической функции;

- изменяться хаотично.

Если остатки модели имеют определенную закономерность в их изменении, то появляется возможность улучшить модель и повысить точность прогнозирования.

Воспроизвести закономерность поведения остатков позволит авторегрессионная модель остатков, основанной на понятии автокорреляции остатков.

Автокорреляция остатков порядка m равна коэффициенту корреляции, рассчитанному между исходными остатками модели и лаговыми остатками порядка m.

Анализ коэффициента автокорреляции проводился в теме 6.

Коэффициент автокорреляции рассчитывается по обычной формуле коэффициента корреляции, только в качестве первой переменной является исходные остатки, а в качестве второй переменной используются лаговые остатки порядка m.

Проверку достоверности коэффициента автокорреляции остатков первого порядка можно производить по упрощенной или по более точной методике.

Упрощенная методика проверка коэффициента автокорреляции совпадает с методикой проверки достоверности обычного парного коэффициента корреляции, которая выполняется в следующей последовательности:

Шаг 1. Выдвигается нулевая гипотеза о том, что r(m) = 0

H₀: r(m) = 0

Шаг 2. Вычисляется r(m).

Ш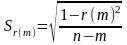 аг 3. Вычисляется ошибка r(m)

Шаг 4. Вычисляется критерий Стьюдента

Ш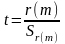 аг 5. Проверяется условие

если t > t( = 0,05, к = n - m - 2), то нулевая гипотеза отвергается с вероятностью 1-. Где t – критерий Стьюдента,  - уровень значимости. В противном случае нулевая гипотеза принимается.

Для более точной проверки достоверности коэффициента автокорреляции остатков первого порядка используется критерий Дарбина- Уотсона (DW) в следующей последовательности:

Шаг 1. Вычисляется критерий Дарбина - Уотсона

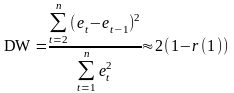
Шаг 2. Определяются по таблицам нижний и верхний пороговые значения соответственно dн и dв, зависящие от числа измерений, уровня значимости и числа объясняемых факторов в модели.

Шаг 3. Проверяются следующие условия:

а) если dн <DW<4-dв, то нулевая гипотеза об отсутствии автокорреляции принимается;

б) если dн <DW<dв или 4-dв <DW<4-dн, то нулевая гипотеза об отсутствии автокорреляции не принимается и не отвергается (область неопределенности критерия);

с) если 0 <DW<dн, то нулевая гипотеза об отсутствии автокорреляции отвергается и утверждается, что имеется положительная автокорреляция остатков;

д) если 4-dн <DW<4, то нулевая гипотеза об отсутствии автокорреляции отвергается и утверждается, что имеется отрицательная автокорреляция остатков.

Критерий DW рассчитывается практически во всех статистических пакетах прикладных программ.

Коэффициент автокорреляции первого порядка обладает следующими свойствами.

Коэффициент автокорреляции может принимать значения от -1 до +1.

Модели, учитывающие автокорреляцию остатков