Основные свойства экономического временного ряда
Приводим основные свойства экономического временного ряда:
1). Текущее состояние экономической системы зависит от прошлых, настоящих и будущих значений переменных этой системы, влияет на будущие значения и не влияет на прошлые значения см. Рис.
Yt+n
Yt
Yt-n
Информация к размышлению. Взаимодействие Уt и Уt+m может носить положительную или отрицательную обратную связь, которая может приводить соответственно к возрастанию или ослаблению колебаний. При этом могут возникнуть стоящие волны, которые можно с успехом разложить в ряд Фурье, так как взаимодействие Уt и Уt+m представляет замкнутую систему с граничными временными интервалами t и t+m, в которых могут быть стоячие волны, по аналогии со струной. Это пожалуй единственный случай, где можно эффективно использовать ряд Фурье по отношению к временным рядам.
2). Для всех явлений в природе между причиной и следствием существует временной лаг или временная задержка.
3). Все временные экономические процессы происходят циклически, которые могут содержать периодические волны: короткие и длинные.
4). «Свежие» значения временного ряда оказывают большее влияние на его прогнозное значение, чем «старые» значения.
5). При построении доверительных интервалов прогноза и уравнения регрессии следует считать боле точным не среднее значение временного ряда, а его последнее значение.
6) В численных значениях временного ряда не должно быть пропусков. Если имеется пропуск, то он восстанавливается средним значением, обычно из ближайших к нему чисел.
7) В некоторой литературе к свойствам временного ряда относят три составляющих временного ряда: тренд, циклическую составляющую и случайное возмущение, которые более подробно изучаются в теме 18.
Статистические характеристики временного ряда
Временные ряды могут иметь следующие статистические характеристики:
1) среднее арифметическое значение;
2) дисперсия,
3) автокорреляция,
4) автокорреляционная функция,
5) периодограмма.
Среднее арифметическое значение временного ряда Уt вычисляется по следующей формуле:
Дисперсия временного ряда вычисляется по формуле
S2= Σ(Уt-Ус)2/(n-1)
Автокорреляция k - ого порядка временного ряда Уt – коэффициент корреляции r(Уt,Уt+k), рассчитанный между исходным временным рядом Уt и этим же временным рядом, только сдвинутым вперед на k дат Уt+k.
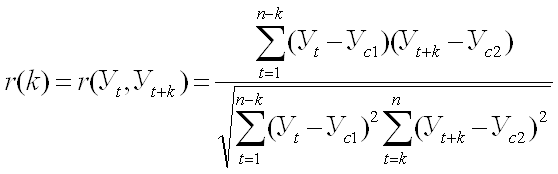
Автокорреляция показывает степень влияния предыдущих значений временного на их последующие значения с временным сдвигом, равным k датам.
Автокорреляционная функция – зависимость коэффициентов автокорреляции от величины их порядка k.
Автокорреляция может изменяться от – 1 до + 1.
Если временный ряд содержит периодическую сезонную составляющую с периодом 4 месяца, то автокорреляционная функция будет иметь наибольшее положительное значение при к = 4, наименьшее отрицательное значение при к = 4/2= 2.
Периодограмма
В эконометрической литературе встречается несколько видов периодограмм. Предлагаем наиболее простой вид периодограмм, основанный на свойстве резонанса.
Периодограмма временного ряда является графиком зависимости ошибки модели Е от периода периодической составляющей Т, чем ближе значение периода Т к периоду периодической составляющей, тем меньше ошибка модели Е.
Модель временного ряда с периодической составляющей имеет следующий вид:
Уt = а0 + а1*t + а2*Соs(2t/T) + а3*Sin(2t/T) + еt
где t- время,
Т – период колебания, изменяющийся от 2 до 2n, которые задает исследователь;
a0, a1, a2, a3 – коэффициенты уравнения регрессии, определяемые МНК.
а0 + а1*t – линейная функция, превращающая нестационарный ряд в стационарный.
Ошибка модели Е определяется с помощью функции ЛИНЕЙН.
Минимумы значений ошибки модели указывают на наличие во временном ряду периодических составляющих с заданными периодами.
Обнаруженные периоды характеризуют периодические составляющие временного ряда.
Основной период имеет наименьшую ошибку модели, а кратные периоды или ложные периоды имеют увеличенную ошибку модели.
Например, квартальная периодическая составляющая 3 мес. порождает эхо на периодах: 32=6 месяцев или полугодовой период, 33 =9 месяцев, 34 =12 месяцев или годовой период и т. д.
