15.4. Метод обращения и разложения в ряд Тейлора
Метод обращения используется в том случае, если исходная модель представлена в виде дроби, где в числителе стоит единица.
Пример 1.
У= 1/(а0+а1*Х+е) – гипербола 2.
Если произвести замену: 1/У=Z1, , то получится новая модель:
Z1= а0+а1*Х+е, коэффициенты которой рассчитываются с помощью функции ЛИНЕЙН.
Метод разложения функции в ряд Тейлора.
Если модель является внутренне нелинейной, т.е. ее нельзя преобразовать в линейную функцию, то эту функцию раскладывают в ряд Тейлора.
Пример 1.
У= а0*Xa1 +е – степенная модель, в которой остатки включены аддитивно, при этом модель становится внутренне нелинейной, так как нельзя привести к линейному виду потому, что нельзя найти логарифм суммы (а0*Xa1 +е).
Однако, с помощью программы «поиск решения» можно найти коэффициенты любых функций, в том числе приведенной в примере.
Поэтому разложение функции в ряд Тейлора становится не актуальным.
Метод разложения функции в ряд Тейлора не получил широкого распространения в эконометрических исследованиях.
Тема 16. Оценка качества нелинейных уравнений регрессии
Показатели качества нелинейных уравнений регрессии
Если определены коэффициенты нелинейной модели, то показателями качества нелинейной модели могут быть:
1. Е - абсолютная ошибка модели,
2. Е% -процент ошибки модели,
3. R2 - коэффициент детерминации,
4. F - критерий Фишера.
Абсолютная и относительная ошибка модели
Показатели качества нелинейной модели – абсолютная и относительная ошибка модели вычисляются по следующим формулам
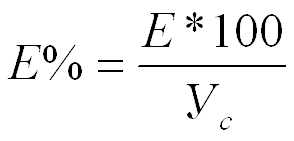
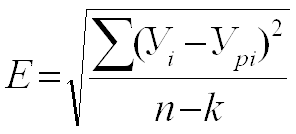
Коэффициент детерминации и критерий Фишера
Показатель качества нелинейной модели: коэффициент детерминации вычисляется по формуле
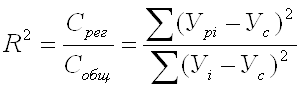
Показатель качества нелинейной модели: Критерий Фишера вычисляется по формуле:
Табличное значение критерия Фишера имеет следующие характеристики:
F(α=0,05; m1 = k-1; m2=n-k)
n - объем выборки,
k - количество коэффициентов в модели, включая свободный коэффициент.
Проверка достоверности нелинейной модели по критерию Фишера имеет стандартную последовательность.
Использование функции ЛИНЕЙН для расчета качества нелинейной модели
Если для линеаризации использовался метод логарифмирования или обращения, то коэффициенты нелинейных моделей и ее характеристики определяются с помощью функции ЛИНЕЙН по преобразованным данным, поэтому полученные характеристики качества модели нельзя использовать для исходных значений.
Тема 17. Временные ряды данных: характеристики и общие понятия Определение временного ряда
Экономический временной ряд – временная последовательность значений показателя экономического процесса.
Временной ряд переменной обозначается как Уt,
где Уt – отдельное наблюдение в фиксированный момент времени t, называемое уровнем ряда,
Уt - является характеристикой экономического процесса
Уt - является случайной величиной,
t (1, …, n) – порядковый номер времени;
(tк+1 – tк) – постоянный временной шаг, через который измеряется значение переменной.
В эконометрике нет ограничений на величину временного шага, обычно им могут быть: сутки, месяц, квартал, год, десятилетия.
n – число уровней, длина, размер, количество значений, временного ряда, но не принято говорить объем выборки.