9.4. Виды ложной корреляции
Известны следующие виды ложной корреляции:
1) ложная корреляция стратификации, связь между двумя неоднородными переменными;
2) ложная корреляция временных рядов;
3) ложная корреляция Пирсона, определение связи между переменными, имеющими общую переменную;
4) ложная корреляция процентных чисел;
5) ложная корреляция неслучайных переменных.
1 – ложная корреляция стратификации (неоднородности) возникает в том случае, если одна или обе переменные Х и У неоднородны и на координатной плоскости наблюдаются несколько облаков точек.
Коэффициент корреляции внутри облаков отличается от коэффициента корреляции для объединенных облаков.
Для устранения этого типа ложной корреляции необходимо рассчитывать коэффициент корреляции для однородных облаков точек данных;
2 – ложная корреляция временных рядов проявляется в том, что два временных ряда испытывают влияние со стороны третьего общего фактора времени.
Для устранения ложной корреляции временных рядов необходимо в каждом временном ряду исключить влияние времени т,е, рассчитать остатки модели, учитывающей влияние времени и затем между полученными остатками вычислить коэффициент корреляции;
3 – ложная корреляция Пирсона возникает в том случае, если Х и У являются расчетными величинами, содержащую общую переменную, например: Х = Х1/Х2, У = Х3/Х2.
Для устранения ложной корреляции Пирсона необходимо использовать фактические значения переменных, а не преобразованных. Обычно для этого используют зависимость выходных показателей деятельности предприятия (прибыль, издержки обращения, товарооборот) от входных показателей предприятия, характеризующих ресурсы предприятия (персонал, основной капитал, оборудование, сырье и материалы);
4 – ложная корреляция процентных чисел проявляется в том случае, если Х и У являются процентными числами, дополняющими друг друга, например Х- процент розничного товарооборота от всего товарооборота, У – процент оптового товарооборота от всего товарооборота, Х+У =100%.
Для устранения ложной корреляции процентных чисел необходимо использовать фактические значения переменных, а не их проценты;
5 – ложная корреляции неслучайных переменных проявляется в том, что значения переменной не являются случайной величиной, а задается исследователем по его воле.
Для устранения ложной корреляции неслучайных переменных следует использовать общепринятые стандартные методики анализа данных. Хотя человеческий фактор в научных исследованиях всегда был и будет присутствовать. Но следует стремиться к объективному анализу данных.
Все четыре типа ложной корреляции очень часто встречаются в научных отчетах и исследованиях.
9.5. Проверка статистической значимости коэффициента корреляции
Проверка статистической гипотезы о равенстве нулю истинного значения коэффициента корреляции необходима для того, чтобы определить наличие или отсутствие линейной тенденции взаимного изменения двух случайных величин.
Этапы проверки статистической значимости коэффициента корреляции.
Этап 1. Выдвигается нулевая гипотеза о том, что значение коэффициента корреляции между Х и У для генеральной совокупности равен нулю
Н0: ρ(Х,У) = 0
Нулевая гипотеза - это предположение о том, что между изучаемыми явлениями нет связи, численные значения характеристик объектов не отличаются между собой.
Нулевые гипотезы проверяются с помощью статистических критериев.
Уровень значимости α (альфа) - означает вероятность совершить ошибку при отклонении нулевой гипотезы.
Этап 2. Вычисляется значение коэффициента корреляции
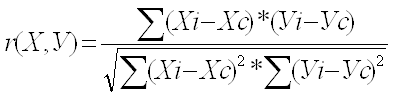
Этап 3. вычисляется критическое значение коэффициента корреляции
t(α=0,05, m= n-2) – табличное значение критерия Стьюдента, на уровне значимости α=0,05 и числе степеней свободы m= n-2.
Этап 4. Сравнение r (x,y) c rкр
Если r (Х,У) > rкр , то нулевая гипотеза отвергается с вероятностью
P=1- α
Если r (Х,У) < rкр , то нулевая гипотеза принимается, но не указывается с какой вероятностью
Простота расчета и анализа коэффициента корреляции позволили широко использовать его в научных исследованиях.
