
- •Национальный минерально-сырьевой университет «Горный»
- •Пояснительная записка к Дипломному проекту Тема: «Проект производства геодезических работ при мониторинге осадок комплекса зданий в Центральном районе г. Санкт-Петербурга»
- •Грунты и Почвы
- •Растительность
- •Гидрография
- •Техническое описание объекта
- •История объекта
- •Причины наблюдения за деформацией
- •Геологическое строение участка работ
- •Топографо-геодезическая изученность
- •Классификация деформация сооружений
- •Методы наблюдения за осадкой сооружения
- •Предрасчет точности
- •Конструкция исходных и деформационныхых знаков
- •Описание геодезических приборов
- •Методика выполнения геометрического нивелирования
- •Периодичность наблюдений
- •Оценка устойчивости исходных реперов
- •4.9.1. Общие сведения
- •4.9.2. Анализ методов оценки устойчивости исходных точек
- •Анализ результатов наблюдений и их оформление
- •Организация и сметная стоимость работ
- •Организация работ
- •Расчет комплексных норм выработки
- •Построение и оптимизация графика производства геодезических работ
- •Потребность в приборах, оборудование, снаряжение и материалах
- •Расчет сметной стоимости геодезических работ
- •Безопасность жизнедеятельности в условиях производства
- •6.1. Характеристика условий и анализ потенциальных опасностей
- •6.2. Обеспечение безопасных при выполнение работ
- •6.2.1. Техника безопасности
- •6.2.2. Общие требования безопасности при камеральных работах
- •6.3. Обеспечение безопасности при чрезвычайных ситуациях
- •6.3.1. План эвакуации при пожаре
- •Охрана окружающей среды
- •Заключение
- •Библиографический список
4.9.2. Анализ методов оценки устойчивости исходных точек
С позиции изложенных требований наиболее известные способы оценки стабильности реперов исходной основы разделены на три группы. К первой группе относятся способы, основанные на анализе изменений превышений, ко второй – способы, использующие определенное математическое условие, накладываемое на результаты измерений и к третьей – способы, использующие принятую гипотезу смещения реперов.
Идея анализа изменений превышений, присущая способам первой группы, довольно наглядно отражена в способе Костехеля.
Вычисление оптимальных высот реперов опорной сети способом Костехеля реализуется в такой последовательности:
уравнивание нивелирной сети как свободной;
определение наиболее устойчивого репера в текущем цикле;
вычисление высот реперов относительно исходной высоты устойчивого репера и уравненных превышений;
расчет степени относительной устойчивости для каждого из реперов сети;
улучшение качества опорной сети путем исключения неустойчивых реперов.
Определение наиболее устойчивого репера в текущем цикле проводится по следующей схеме.
Если величина разности превышений vi = hi – h отражает суммарное влияние осадок реперов за период между первым и i - ым циклами нивелирования, то репер, для которого [ vv ] = min, является наиболее устойчивым и его высота, полученная в нулевом цикле принимается за исходную при вычислениях высот осадочных реперов в текущем цикле наблюдений.
При вычислении разности превышений v всех звеньев сети за исходные принимаются последовательно все три глубинных опорных репера.
Для определения степени относительной устойчивости и неустойчивости репера опорной сети вычисляется осадка репера:
i = Hi – H1, где
Hi
и
H1
– высоты
репера из нулевого и
i
– го
циклов наблюдений. Если
![]() > 1, то репер считается устойчивым и
наоборот.
> 1, то репер считается устойчивым и
наоборот.
Средняя
квадратическая погрешность ms
= mh![]() = ± 0.49
= ± 0.49![]() ,
где
,
где
mh – средняя квадратическая погрешность превышения на станции, равная для проектируемой сети ± 0.35 мм;
P - обратный вес эквивалентного хода, выраженный числом штативов.
Переходя к предельным значениям имеем
пред = ± 0.99 .
Методика анализа устойчивости реперов, предложенная П.Марчаком заключается в следующем:
Уравнивается нивелирная сеть как свободная.
Находится фактическая разность превышения для отдельных звеньев hi = hi – h1 и фактическая разность hр превышений от начала нивелирного хода до данного репера.
Подсчитывается среднее арифметическое
 из разностей превышений, не превышающих
hпред,
каждого репера над начальным, гдеK
– число устойчивых реперов,
из разностей превышений, не превышающих
hпред,
каждого репера над начальным, гдеK
– число устойчивых реперов,
hпред
≤ 2 mh
![]() ,
где n
– число станций считаются от начала до
середины хода нарастающим итогом.
,
где n
– число станций считаются от начала до
середины хода нарастающим итогом.
Подсчитываются исправленные разности hо превышений или редуцированные вертикальные перемещения реперов по формуле:
hо = hр - ( ).
В итоге за стабильные предполагается принимать только те глубинные реперы опорной сети, неподвижность которых будет подтверждена обоими вышеизложенными методами.
В случае неустойчивости глубинного репера в отдельном цикле измерений в работе будет использована вновь полученная высота.
Чтобы избежать вычисления дополнительных превышений, анализ производится, используя смещения реперов относительно друг друга, при этом для удобства работы и наглядности анализа применяется табличная форма представления материала, что и предложено с способе И.Рунова.
Табличная форма представления данных используется и в способе А.Зеленского, В.Дорофеевой, однако таблица составляется с использованием превышений и без учета свойств кососимметрической матрицы, облегчающей ее составление, что увеличивает трудоемкость работы.
Изложенные способы характерны тем, что они используют для анализа все возможные изменения взаимного положения реперов и позволяют определить стабильный репер в каждом цикле наблюдений, что соответствует изложенным выше требованиям к оценке устойчивости реперов исходной основы.
Данные об устойчивости системы исходных реперов можно получить путем исследования корреляционной взаимосвязи между превышениями в разных циклах наблюдений, т.е. анализа коэффициентов корреляции. Численные зависимости между превышениями, связанными осадками опорных пунктов, находят из уравнений регрессии.
Метод
заключается в следующем: из 33 циклов
наблюдений вычисляют средние значения
превышений
![]() и отклонений
и отклонений
![]() от них:
от них:
1 = h1 - 1; 2 = h2 - 2; 3 = h3 - 3;
а
также величины: [![]() ]
, [
]
, [![]() ]
, [
]
, [![]() ].
].
Определяют вторые центральные моменты:
![]() =
=
![]()
=
![]()
=
![]()
где n – число циклов наблюдений (n = 33), и первые смешанные центральные моменты:
=
![]()
=
![]()
=
![]() .
.
Находят величины средних квадратических отклонений (стандарты), извлекают корень из вторых центральных моментов:
![]() h1
=
h1
=
![]()
h2
=
![]()
h3=
![]() .
.
Вычисляют коэффициенты корреляции:
а) парные (между двумя превышениями):
rh1
h2
=
![]() ;
;
rh1
h3
=
![]() ;
;
rh2
h3
=
![]() ;
;
б) частные:
при связи h1 и h2 и постоянном h3
rh1
h2
h3
=
 ;
;
при связи h1 и h3 и постоянном h2
rh1
h2
h3
=
 ;
;
При связи h2 и h3 и постоянном h1
rh1
h2
h3
=
 ;
;
в) множественные:
Rh1
h2 h3
=
 ;
;
Rh2
h1 h3
=
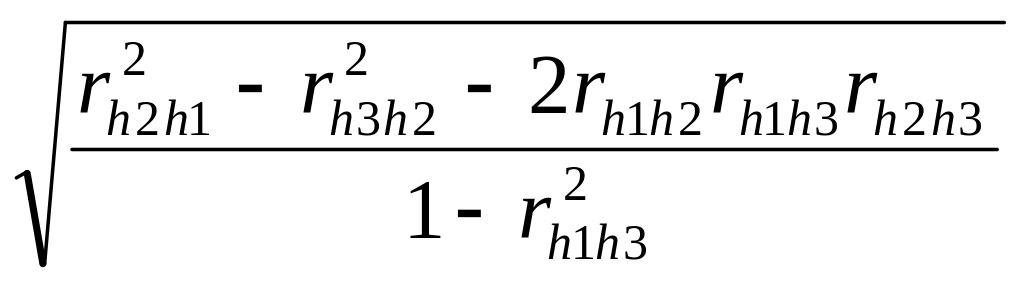 ;
;
Rh3
h1 h2
=
 .
.
Проверяют значимость коэффициентов корреляции, вычисляя их среднее квадратическое отклонение:
![]() =
=
![]() .
.
Коэффициенты считаются значимыми, если
rh > 3 .
Из анализа коэффициентов корреляции следует, что наиболее тесная взаимосвязь имеется между превышениями h1 и h2. Превышение h3 мало влияет на связь h1 и h2. Отрицательный парный коэффициент rh1 h3 = - 0,69 и частный rh1 h2 h3 = - 0,55 показывают, что с уменьшением h1 возрастает величина h2, а так как h1 < 0 и h2 > 0, то, следовательно, по абсолютной величине оба превышения увеличиваются. А обозначает, что Rр2 дает осадку.
Из способов второй группы, использующих определенное математическое условие, накладываемое на результаты измерений, относится способ В.Черникова. В этом способе отметки реперов в каждом цикле вычисляются как вероятнейшие под условием минимума суммы квадратов отклонений отметок от их значений в исходом цикле. В основу такого решения положена идея неизменности средней высоты реперов исходной основы, которая исходит их того, что если нет оснований судить об устойчивости реперов, каждый из которых с одинаковой вероятностью может изменить свою высоту, то целесообразно принять неизменной среднюю высоту этих реперов.
К способам, использующим определенную гипотезу смещения реперов, относится способ Л.Серебряковой. В нем предлагается исходить из предположения, что реперы подвержены только осадке, и за исходный принимать тот репер, который имеет наименьшую осадку, и относительно него определять смещения остальных реперов с ошибкой, равной этой самой меньшей осадке.
