1.2 Двухмассовая модель, как объект управления (аналоговый вариант)
В современной теории управления наиболее часто используется два вида переменных (две модели).
1. Переменные «входы-выходы». Суть этой модели заключается в том, что реальные физические величины, участвующие в системе, представляются в виде, так называемых, переменных «входы» и переменных «выходы», то есть, в измеряемых и нужных в данных системах физических величин. Этот вид модели хорош своей «физичностью», однако, в случаях сложных систем не всегда может быть использован.
2. Переменные «состояния». Система представляется в виде переменных, связанных с входами и выходами, и обеспечивает их совместимость, и, благодаря этому, удобное математическое описание весьма разнообразных величин.
Преимущество 2-го вида модели особенно ощутимо при работе со сложными системами с целью создания оптимальных алгоритмов управления.
1.2.1 Динамическая модель двухмассовой системы в переменных «входы-выходы». Структурная схема динамической модели
Для этого представим уравнения (1) - (3) в
виде системы дифференциальных уравнений,
где оператор
обозначает 1-ую производную.
Кроме того, определим понятие «переменные», представляющие собой реальные воздействия, и, при этом, изменяющиеся в зависимости от поставленной перед собой задачи.
Выберем переменные, которые будем
считать «входами» (
),
и переменные, которые будем считать
«выходами» (
).
В одной из очевидных постановок задачи
входными переменными будут являться
вращающий электромагнитный момент
,
который формируется с помощью ЭД, а
также моменты сопротивлений
и
,
создаваемые, в основном, силами трения.
Выходной переменной будет являться
скорость второй массы
.
Продифференцируем уравнение (1):
Тогда введя понятие «оператор», можно представить уравнения (1) - (3) в операторной форме:
Решение задачи сводится к представлению
графического образа системы, который
состоит из совокупности графических
образов отдельных звеньев и в них
содержатся переменные (
,
,
,
,
,
),
параметры (
,
,
)
и оператор (
).
Условимся обозначать переменные
стрелками; параметры и оператор,
образующие алгебраические выражения
заключать в прямоугольные рамки; а для
алгебраического суммирования использовать
окружности, иногда с секторами, при этом
слагаемые обозначаются стрелками
подходящими к не заштрихованным секторам
окружности, вычитаемые - стрелками
подходящими к заштрихованным секторам
окружности, а сумму - стрелками отходящими
от окружности.
Представим модель согласно уравнению (4).
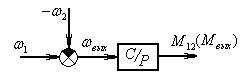
Рис.3а Динамическая модель (
)
Модель, согласно уравнению (5):
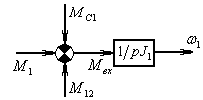
Рис.3б Динамическая модель (
)
Модель, согласно уравнению (6):
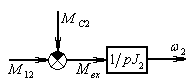
Рис.3в Динамическая модель (
)
В графических образах все выражения,
записанные в прямоугольных рамках,
представляют собой выражения вида
(интегратор). Поэтому все три представленных
звена можно отнести к звеньям интегрирующего
типа. Для решения поставленный задачи
объединим графические звенья в один
графический образ - структурную схему
системы. Для этого введем ещё одно
обозначение - узел, который будем
обозначать точкой, при этом, отходящие
от одного узла стрелки соответствуют
одной и той же переменной.
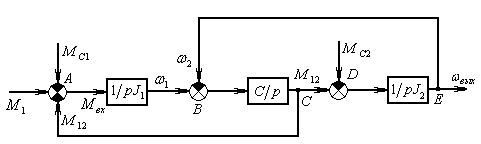
Рис.4 Структурная схема двухмассовой механической системы в переменных «входы-выходы»
Выражение, заключённое в прямоугольные рамки, представляет собой отношение выходной величины к входной, и называется передаточной функцией звена.
Поставим перед собой задачу нахождения общей передаточной функции системы.
Для этого используют операцию агрегирования, т.е. свёртывания структурной схемы с целью представления её в виде одного звена.