1. Линейная (прямая)

Y_x=A + BX (2.1)

Данное уравнение позволяет определить вектор развития:

Рис. 2. 1. Трендовая модель развития экономического процесса, по линейной зависимости

параметр B с плюсом – рост, B с минусом – спад. Он указывает на то, что процесс развивается равномерно, без ускорения и замедления. Модель тренда по линейной функции отражена на рис. 2.1.

2. Парабола второго порядка

Yx=A + B₁X + B₂X² (2.2)

Данная модель позволяет выявить не только скорость развития (B₁)_, но и его ускорение (B₂)_. В зависимости от знаков параметров определяется вектор развития (рост, спад, ускорение, замедление). Применение данной модели возможно в широком диапазоне.

Криволинейную тенденцию часто хорошо аппроксимирует парабола более высокого, чем второй, порядка:

Yx=A + B₁X + B₂X² +…+ B_nXⁿ (2.3)

Параболический рост, а затем спад отражены на рис. 2.2.

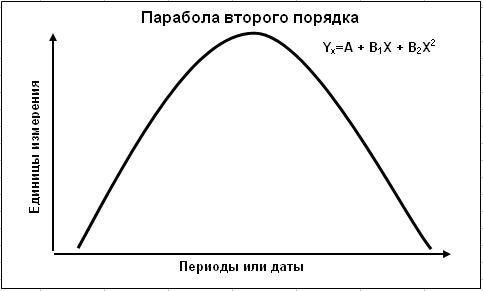
Рис. 2. 2. Модель тенденции развития экономического процесса по параболе второго порядка

3. Экспонента

В тех случаях, когда прирост зависит от величины основания функции, обычно используют сглаживание по экспоненциальной кривой, иногда называемой экспонентой. Она обычно отражает нарастание приростов. Ее формула:

Yx=AE^BX или, в линеаризированном виде Lg Yx = Lg A + BX (2.4)

Моделирование тренда по экспоненте в графической форме представлено на рис. 2.3.

Рис. 2. 3. Трендовая модель тенденции развития экономического процесса по экспоненте

4. Степенная функция

Часто встречаются тенденции, которые можно отразить уравнением степенной функций:

Yx = AB^X или в линейном виде Lg Yx = Lg A + X Lg B (2.4)

Модель тренда по степенной функции приведена на рис. 2.4.

Рис. 2. 4. Трендовая модель тенденции развития экономического процесса по степенной функции

5. Показательная функции

Тенденции, отображаемые уравнением показательной функции, выглядят обратными степенной:

Рис. 2. 5. Трендовая модель тенденции развития экономического процесса по показательной функции

Yx = AX^B или в линейном виде Lg Yx = Lg A + B Lg X (2.5)

Модель тренда по показательной функции приведена на рис. 2.5.

6. Логарифмическая (полулогарифмическая) функция

Если равномерный или ускоренный рост параметров рынка сменяется замедлением или затуханием развития, то такую тенденцию достаточно надежно отражает логарифмическая функция типа

Yx = A + Lg Х (2.6)

В графической форме подобная трендовая модель показана на рис. 2.6.

Рис. 2. 6. Трендовая модель тенденции развития экономического процесса по логарифмической функции

7. Гипербола

Тенденция к спаду динамики экономического процесса с нарастающим замедлением к концу периода, хорошо отображается функцией гиперболы:

Yx = A + В * 1/Х (2.6)

Графическая форма модели гиперболического тренда приведена на рис. 2.7.

Трендовые модели используются также для краткосрочных прогнозов, когда есть вероятность инерционного развития рынка. При этом, исходят из того, что сложившиеся в прошлом тенденции при соответствующих условиях можно распространить (экстраполировать) на прогнозируемый период. В формулу уравнения подставляется номер последующего прогнозируемого периода. Для долгосрочного периода, когда существенно меняются рыночные условия и окружающая среда, этот метод мало подходит. Кроме того, дополнительные сложности возникают, когда необходимо учитывать сезонность. Несколько позже будет рассмотрена данная проблема.

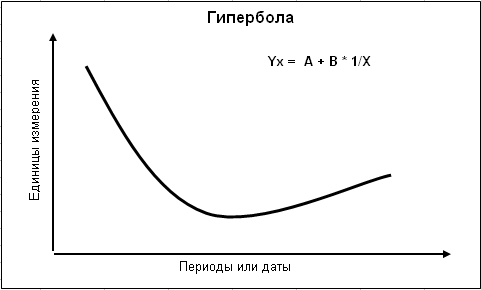
Рис. 2. 7. Трендовая модель тенденции развития экономического процесса по гиперболе

Excel предоставляет пользователю широкие возможности построения таких моделей и прогнозирования поведения объекта. Это, прежде всего методы построения линий трендов для известных значений временных рядов², методы статистического анализа данных наблюдений, методы линейного и динамического программирования ("Поиск решения") и др.

Рассмотрим применение этих методов на нескольких примерах, имеющих отношение к деятельности торговых предприятий.

Каждую задачу выполняйте на отдельном листе рабочей книги. Имена листам давайте в соответствии с номером задания – 1.1; 1.2…. или Зад 1.1.: Зад. 1.2…