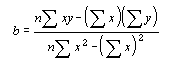- •Введение
- •1. Понятие, задачи, принципы и методы прогнозирования и планирования
- •1.1.Понятие, задачи и принципы прогнозирования и планирования
- •1.2.Классификация методов прогнозирования
- •1.3.Экстраполяционные методы прогнозирования
- •1.4.Статистические методы прогнозирования
- •1.5.Экспертные методы прогнозирования
- •1.6.Вопросы для самоподготовки
- •2. Анализ и прогноз рядов наблюдений
- •2.1. Основные типы линий тренда
- •1. Линейная (прямая)
- •2. Парабола второго порядка
- •3. Экспонента
- •2.2. Построение линии тренда расходов на продукты питания в зависимости от уровня дохода семьи Задание 1. Построение линии тренда
- •2.3. Анализ данных с помощью пакета анализа данных еxcel
- •Задание 2. Генерация случайных чисел
- •Задание 3. Сглаживание обрабатываемых данных
- •2.4. Использование процедуры «поиск решения» для подбора коэффициентов функции аппроксимации данных наблюдений
- •Задание 4. Подбор коэффициентов функции аппроксимации
- •1. Сначала представьте имеющиеся данные в виде непрерывного ряда наблюдений и по этим данным постройте график и линию тренда изменения товарооборота за период 2002-2004гг.
- •2. После того, как данные наблюдений представлены в виде непрерывного ряда, постройте диаграмму (рис. 2.34) и найдите уравнение линии тренда (как было описано выше в зад. 1.1).
- •3. Используя Пакет анализа, выполните сглаживание значений ряда наблюдений y1 методами Скользящего среднего и Экспоненциального сглаживания (как в задании 1.3).
- •4. Для исследования временных изменений ряда наблюдений, например, сезонных, выполните следующие действия:
- •2.5. Вопросы для самоподготовки
- •3. Статистический анализ и прогноз рядов наблюдений
- •3.1. Линейная и экспоненциальная аппроксимация данных
- •3.2. Функции линейн() и лгрфприбл()
- •Дополнительная статистика
- •Задание 5. Прогнозирование с помощью функций линейн() и лгрфприбл(),
- •3.3. Функции прогноза тенденция() и рост()
- •Задание 6. Прогнозирование с помощью функций тенденция() и рост()
- •3.4. Функции прогноза сТандоткл() и доверит()
- •3.5. Функция Коррел()
- •Задание 7. Прогнозирование с помощью функции коррел
- •3.6. Функции наклон() и отрезок()
- •Задание 8. Прогнозирование с помощью функции наклон()
- •Синтаксис функции отрезок (Известные_значения_x; Известные_значения_y) Аргументы функции отрезок()
- •Задание 9. Прогнозирование с помощью функции отрезок()
- •3.7. Вопросы для самоподготовки
- •4. Анализ и прогнозирование в инвестиционном проектировании
- •1.7.4.1. Методы анализа и прогнозирования в инвестиционном проектировании
- •4.2. Алгоритм построения прогнозной модели
- •4.3. Интервальное экспертное прогнозирование
- •Задание 10. Пример выполнения интервального экспертного прогнозирования
- •4.4. Вопросы для самоподготовки
- •2.Использование элементов управления для графического прогнозирования
- •5.1. Использования элементов управления панели "форма"
- •Задание 11. Использование элементов управления панели «Форма»
- •2.1.Вопросы для самоподготовки
- •3.Подбор парметров16
- •3.1.Подбор параметра в таблице
- •Задание 12. Выполнение процедуры Подбор параметра
- •Задание 13. Выполнение процедуры Подбор параметра для поиска корней уравнения
- •3.2.Таблицы подстановки
- •Задание 14. Таблица с одним входом
- •Задание 15. Таблица с двумя входами
- •3.3.Сценарии
- •Задание 16. Создание сценариев
- •3.4.Вопросы для самоподготовки
- •4.Экспертные оценки
- •4.1.Подбор состава экспертов
- •4.2. Методы проведения экспертизы
- •Задание 16. Непосредственное назначение коэффициентов веса
- •Задание 17. Оценка важности параметра в баллах
- •Задание 18. Метод парных сравнений
- •Задание 19. Определение усредненных значений результатов экспертизы с использованием процедуры консолидации
- •4.3.Метод «делфи»
- •4.4.Вопросы для самоподготовки
- •8. Указания по выполнению самостоятельной работы
- •4.5.Порядок выбора варианта и данных
- •4.6.Варианты самостоятельных заданий Задание для самостоятельной работы № 1
- •Задание для самостоятельной работы № 2
- •Задание для самостоятельной работы № 3
- •Задание для самостоятельной работы № 4
- •Литература
3.5. Функция Коррел()
Для оценки качества сделанного прогноза (рассчитанного уравнения прогноза) может быть использована функция КОРРЕЛ(), которая возвращает коэффициент корреляции меджу интервалами ячеек Массив1 и Массив2.
Коэффициент корреляции используется для определения степени взаимосвязи между двумя свойствами (рядами наблюдений). Например, можно оценить зависимость между количеством проданного товара и количеством продавцов и др.
Синтаксис функции КОРРЕЛ (Массив1;Массив2)
Аргументы функции КОРРЕЛ
Массив1 — это интервал ячеек первого ряда данных (например, ряда наблюдений).
Массив2 — это второй интервал ячеек со значениями другого ряда (например, ряда, рассчитанного по уравнению прогноза).
Замечания
Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
Если Массив1 и Массив2 имеют различное количество точек данных, то функция КОРРЕЛ возвращает значение ошибки #Н/Д.
Если Массив1 либо Массив2 пуст, или если σ (стандартное отклонение) их значений равно нулю, то функция КОРРЕЛ возвращает значение ошибки #ДЕЛ/0!
Уравнение для коэффициента корреляции имеет следующий вид:
 (3.7)
(3.7)
где
![]() (3.8)
(3.8)
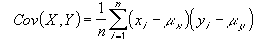 (3.9)
(3.9)
Задание 7. Прогнозирование с помощью функции коррел
Имеются следующие данные о количестве продавцов и товарообороте магазина за 2004 год (рис. 3.15):

Рис. 3. 15. Таблица для расчетов коэффициента корреляции
Для определения связи между количеством продавцов и товарооборотом магазинов рассчитайте коэффициент корреляции между двумя рядами данных:
Установите курсор мыши в ячейку, куда должны быть возвращены результаты расчета коэффициента корреляции – D14.
Вызовите статистическую функцию КОРРЕЛ().
В открывшемся диалоговом окне «Аргументы функции» в окна «Массив1» и «Массив2» (рис. 3.16) введите адреса ячеек, содержащие данные наблюдений и результатов прогноза (соответственно C2:C13 и D2:D13).

Рис. 3. 16. Диалоговое окно задания аргументов функции КОРРЕЛ
Щелкните на кнопке «ОК»
В результате выполненных действий в ячейку будет возвращено значение коэффициента корреляции между количеством продавцов и величиной товарооборота, равное 0,949736179, что показывает очень тесную связь между показателями.
3.6. Функции наклон() и отрезок()
Достаточно часто при анализе экономических данных вам совершенно не обязательно знать вид уравнения прогноза, а достаточно знание только значений отдельных коэффициентов. Например, при анализе ряда данных, характеризующих затраты на производство изделий необходимо знать величину постоянных или переменных издержек. Для этих целей можно использовать статистические функции НАКЛОН() и ОТРЕЗОК().
Функция НАКЛОН() возвращает наклон линии линейной регрессии для точек, данных в аргументах: Известные_значения_Y и Известные_значения_X. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой, то есть наклон — это скорость изменения значений вдоль прямой.
Синтаксис функции
НАКЛОН (Известные_значения_ y; Известные_значения_ x)
Аргументы функции НАКЛОН()
Известные_значения_y — массив или интервал ячеек, содержащих числовые зависимые точки данных.
Известные_значения_x — множество независимых точек данных.
Замечания
Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
Если Известные_значения_y и Известные_значения_x пусты или содержат различное число точек данных, то функция НАКЛОН() возвращает значение ошибки #Н/Д.
Уравнение наклона линии регрессии имеет следующий вид:
|
|
(3.10) |