3.4. Функции прогноза сТандоткл() и доверит()

Продолжение описания решения Задания 6

Для ячеек D16:Е16 определите стандартное отклонение - меру того, насколько широко разбросаны точки данных относительно их среднего.

Синтаксис функции СТАНДОТКЛОН (число1; число2; ...)

Аргументы функции СТАНДОТКЛОН

• Число1, число2, ... — от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно также использовать массив или ссылку на массив.

СТАНДОТКЛОН использует следующую формулу:

(3.6)

Вид окна функции СТАНДОТКЛОН для ячейки С16 приведен на рис. 3.12, а полученный результат – на рис. 3.14

 СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.

Стандартное отклонение вычисляется с использованием "несмещенного" или "n-1" метода.

 Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текст и логические значения игнорироваться не должны, следует использовать функцию рабочего листа СТАНДОТКЛОНА.

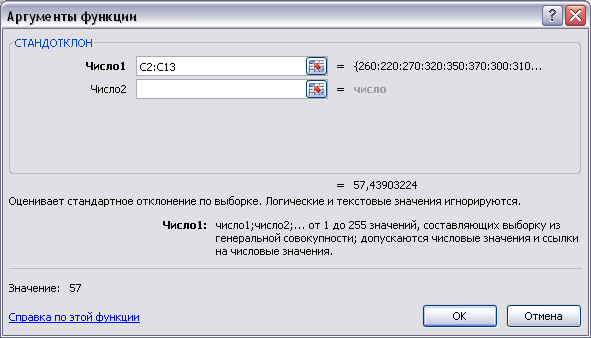
Рис. 3. 12. Окно функции СТАНДОТКЛ для расчета насколько разбросаны точки данных относительно их среднего значения

• Для ячеек D17:F17 определите доверительный интервал - это интервал с обеих сторон от среднего.

Синтаксис функции ДОВЕРИТ (Альфа; Станд_откл; Размер)

Аргументы функции ДОВЕРИТ

• Альфа   — это уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется 100*(1 - альфа) процентам, или, другими словами, альфа равное 0,05 означает 95% уровень надежности.

• Станд_откл   — это стандартное отклонение генеральной совокупности для интервала данных, предполагается известным.

• Размер   — это размер выборки.

 Если какой-либо из аргументов не является числом, то функция ДОВЕРИТ возвращает значение ошибки #ЗНАЧ!.

Если Альфа  ≤  0 или Альфа  ≥  1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Если Станд_откл  ≤  0, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Если размер не целое, то оно усекается.

Если размер  <  1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Предположим, что в нашем примере среднемесячный товарооборот 279 млн. руб. со стандартным отклонением для генеральной совокупности равным 57 млн. руб. В таком случае, мы можем быть на 95 процентов уверены в том, что среднее для генеральной совокупности находится в интервале: ± 32 млн. руб.

Вид окна функции ДОВЕРИТ для ячейки С16, приведен на рис. 3.13, а полученное значение на рис. 3.14.

 Внимание. Для расчета доверительного интервала для столбцов D и Е в поле Размер надо вводить значение ячейки А14, так как в расчетах используется 13 значений.

Рис. 3. 13. Окно функции ДОВЕРИТ для расчета интервала разброса данных от среднего значения

Таблица, полученная в результате всех вычислений, приведена на рис 3.14.

Самостоятельно сделайте выводы о том, в каких случаях можно применять те или иные методы статистического анализа.

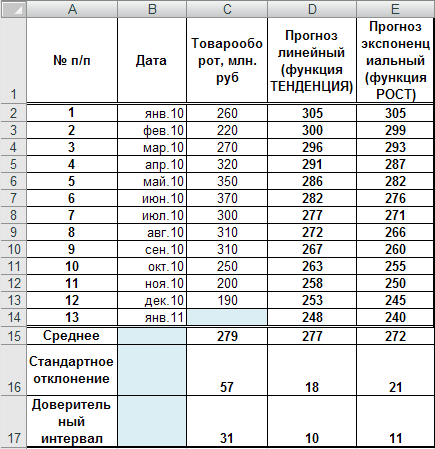
Рис. 3. 14. Итоговая таблица с результатами вычислений