
- •Введение
- •1. Понятие, задачи, принципы и методы прогнозирования и планирования
- •1.1.Понятие, задачи и принципы прогнозирования и планирования
- •1.2.Классификация методов прогнозирования
- •1.3.Экстраполяционные методы прогнозирования
- •1.4.Статистические методы прогнозирования
- •1.5.Экспертные методы прогнозирования
- •1.6.Вопросы для самоподготовки
- •2. Анализ и прогноз рядов наблюдений
- •2.1. Основные типы линий тренда
- •1. Линейная (прямая)
- •2. Парабола второго порядка
- •3. Экспонента
- •2.2. Построение линии тренда расходов на продукты питания в зависимости от уровня дохода семьи Задание 1. Построение линии тренда
- •2.3. Анализ данных с помощью пакета анализа данных еxcel
- •Задание 2. Генерация случайных чисел
- •Задание 3. Сглаживание обрабатываемых данных
- •2.4. Использование процедуры «поиск решения» для подбора коэффициентов функции аппроксимации данных наблюдений
- •Задание 4. Подбор коэффициентов функции аппроксимации
- •1. Сначала представьте имеющиеся данные в виде непрерывного ряда наблюдений и по этим данным постройте график и линию тренда изменения товарооборота за период 2002-2004гг.
- •2. После того, как данные наблюдений представлены в виде непрерывного ряда, постройте диаграмму (рис. 2.34) и найдите уравнение линии тренда (как было описано выше в зад. 1.1).
- •3. Используя Пакет анализа, выполните сглаживание значений ряда наблюдений y1 методами Скользящего среднего и Экспоненциального сглаживания (как в задании 1.3).
- •4. Для исследования временных изменений ряда наблюдений, например, сезонных, выполните следующие действия:
- •2.5. Вопросы для самоподготовки
- •3. Статистический анализ и прогноз рядов наблюдений
- •3.1. Линейная и экспоненциальная аппроксимация данных
- •3.2. Функции линейн() и лгрфприбл()
- •Дополнительная статистика
- •Задание 5. Прогнозирование с помощью функций линейн() и лгрфприбл(),
- •3.3. Функции прогноза тенденция() и рост()
- •Задание 6. Прогнозирование с помощью функций тенденция() и рост()
- •3.4. Функции прогноза сТандоткл() и доверит()
- •3.5. Функция Коррел()
- •Задание 7. Прогнозирование с помощью функции коррел
- •3.6. Функции наклон() и отрезок()
- •Задание 8. Прогнозирование с помощью функции наклон()
- •Синтаксис функции отрезок (Известные_значения_x; Известные_значения_y) Аргументы функции отрезок()
- •Задание 9. Прогнозирование с помощью функции отрезок()
- •3.7. Вопросы для самоподготовки
- •4. Анализ и прогнозирование в инвестиционном проектировании
- •1.7.4.1. Методы анализа и прогнозирования в инвестиционном проектировании
- •4.2. Алгоритм построения прогнозной модели
- •4.3. Интервальное экспертное прогнозирование
- •Задание 10. Пример выполнения интервального экспертного прогнозирования
- •4.4. Вопросы для самоподготовки
- •2.Использование элементов управления для графического прогнозирования
- •5.1. Использования элементов управления панели "форма"
- •Задание 11. Использование элементов управления панели «Форма»
- •2.1.Вопросы для самоподготовки
- •3.Подбор парметров16
- •3.1.Подбор параметра в таблице
- •Задание 12. Выполнение процедуры Подбор параметра
- •Задание 13. Выполнение процедуры Подбор параметра для поиска корней уравнения
- •3.2.Таблицы подстановки
- •Задание 14. Таблица с одним входом
- •Задание 15. Таблица с двумя входами
- •3.3.Сценарии
- •Задание 16. Создание сценариев
- •3.4.Вопросы для самоподготовки
- •4.Экспертные оценки
- •4.1.Подбор состава экспертов
- •4.2. Методы проведения экспертизы
- •Задание 16. Непосредственное назначение коэффициентов веса
- •Задание 17. Оценка важности параметра в баллах
- •Задание 18. Метод парных сравнений
- •Задание 19. Определение усредненных значений результатов экспертизы с использованием процедуры консолидации
- •4.3.Метод «делфи»
- •4.4.Вопросы для самоподготовки
- •8. Указания по выполнению самостоятельной работы
- •4.5.Порядок выбора варианта и данных
- •4.6.Варианты самостоятельных заданий Задание для самостоятельной работы № 1
- •Задание для самостоятельной работы № 2
- •Задание для самостоятельной работы № 3
- •Задание для самостоятельной работы № 4
- •Литература
3.3. Функции прогноза тенденция() и рост()
В тех случаях, когда вас интересует прогноз значений Y на какой-то интервал времени (или другой отрезок независимых переменных), Excel предлагает использование функций прогноза, основанных на линейном или экспоненциальном приближении13.
Функция ТЕНДЕНЦИЯ() вычисляет значения в соответствии с линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов) массивы известных значений Y и известных значений Х. Возвращает значения Y, в соответствии с этой прямой для заданного массива новые значения Х.
Функция ПРЕДСКАЗ() вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это Y -значение, соответствующее заданному Х - значению. Известные значения — это Х - и Y -значения, а новое значение предсказывается с использованием линейной регрессии. Эта функцию рассчитывает прогнозные данные аналогично функции ТЕНДЕНЦИЯ(). Полученные значения одинаковы.
Функция РОСТ() рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Функция РОСТ возвращает значения Y для последовательности новых значений Х, задаваемых с помощью существующих Х- и Y-значений. Функция рабочего листа РОСТ может применяться также для аппроксимации существующих Х- и Y-значений экспоненциальной кривой.
Синтаксис функций ТЕНДЕНЦИЯ() и РОСТ()
ТЕНДЕНЦИЯ (Известные значения Y; Известные значения Х; Новые значения Х; Константа).
Функция возвращает значения Y в соответствии с линейным трендом.
РОСТ (Известные значения Y; Известные значения Х; Новые значения Х; Константа).
Функция возвращает значения Y в соответствии с экспоненциальным трендом.
Аргументы функций ТЕНДЕНЦИЯ() и РОСТ()
«Известные значения Y» - это множество значений Y, которые уже известны для соотношения Y=m*x+b (2.1) или Y=b*m^x (2.40) - при экспоненциальном сглаживании.
«Известные значения X» - это необязательное множество значений Х, которые уже известны для соотношения Y=m*x+b (2.1) или Y=b*m^x (2.40) - при экспоненциальном сглаживании.
«Новые значения X» - это новые значения X, для которых должны быть определены значения Y.
«Константа» - это логическое выражение, которая при значении равном «1» (истина) указывает на необходимость вычисления константы b. Если константа равна «0» (ложь), то b полагается равным «0» или «1» при экспоненциальном сглаживании.
Внимание. Формулы, которые возвращают массивы, должны вводится как формулы массивов, после выделения подходящего числа ячеек.
Задание 6. Прогнозирование с помощью функций тенденция() и рост()
Имеются следующие данные о товарообороте крупного магазина за 2010 год (рис. 3.6):
Для прогнозирования значения Y для нового значения Х (значения, которое не содержится в исследуемом ряде наблюдений) выполните следующее (в нашем случае – это прогноз на январь 2011 года):

Рис. 3. 6. Таблица с начальными данными
Курсор установите в ячейку D14.
Вызовите функцию ТЕНДЕНЦИЯ() (категория функция «Статистические»).
В диалоговом окне Аргументы функции (рис. 3.7) введите необходимые адреса:
В окно «Известные значения_Y» введите адреса ячеек, содержащих известные значения товарооборотов за 2010 год - Y (С2:С13).
В окно «Известные значения_Х», введите адреса ячеек известных дат - Х (В2:В13)
В окно «Новые значения_Х» введите адрес ячейки, содержащей новое значение расчетного месяца (января 2011) - Х (В14).
Щелкните на кнопке «ОК».
Примечание. В предыдущих версиях Excel даты не всегда корректно влияли на конечный результат, поэтому вместо них приходилось использовать значения номеров месяцев 2010 года (А2:А13). Попробуйте пересчитать формулу с использованием этих номеров, например, в ячейке D15, и вы увидите, что результат будет аналогичным. Не забудьте, затем очистить ячейку D15.
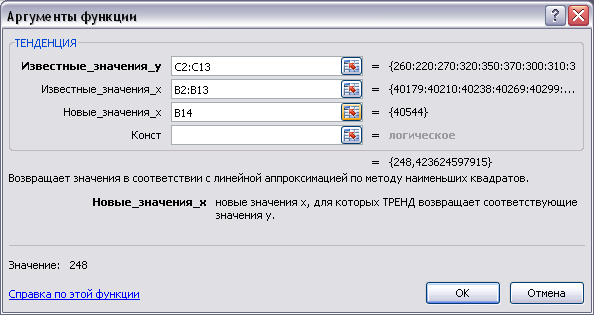
Рис. 3. 7. Окно для ввода аргументов функции ТЕНДЕНЦИЯ() для одного значения
Полученный результат округлите до целых чисел кнопкой
 Уменьшить
разрядность.
Должно получиться число 249.
Уменьшить
разрядность.
Должно получиться число 249.Аналогично выполните прогнозирование величины товарооборота на январь 2011 года для магазина, используя функцию РОСТ() (ячейка Е14). Для этого последовательно выполните вышеописанные действия, заменив функцию ТЕНДЕНЦИЯ() на функцию РОСТ(). В результате будет получено значение -240.
Полученные значения 249 и 240 отличаются незначительно друг от друга (на 3,6%), но довольно далеки от величины товарооборота за декабрь 2011 года, равного 190.
Попробуйте разобраться, почему это так. Для этого рассчитайте с помощью функций ТЕНДЕНЦИЯ() и РОСТ() теоретические значения товарооборота за весь 2004 год.
В ячейки D2:D13 и E2:E13 введите функции ТЕНДЕНЦИЯ() и РОСТ() как формулы массива соответственно. Рассмотрим этот процесс подробно на функции ТЕНДЕНЦИЯ().
Выделите интервал ячеек, куда должны быть возвращены новые значения Y - D2:D13.
Откройте Мастер функций и в категории Статистические выберите функцию ТЕНДЕНЦИЯ().
Введите все необходимые данные, как показано на рис. 3.8.

Рис. 3. 8. Окно для ввода аргументов функции ТЕНДЕНЦИЯ()
Завершите ввод данных одновременным нажатием на клавиши CTRL + SHIFT + ENTER, что позволит посчитать функцию ТЕНДЕНЦИЯ() как формулу массива.
Округлите полученные данные до целых чисел.
Аналогичные действия выполните для ячеек E2:E13, куда будет введена функция РОСТ() (рис. 3.9).
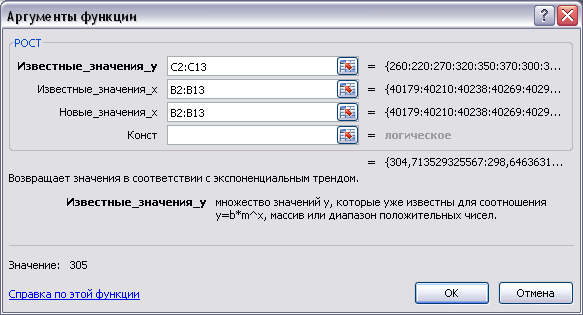
Рис. 3. 9. Окно для ввода аргументов функции РОСТ()
Как видно из сравнения фактических и прогнозных данных (рис. 3.14) между ними существуют значительные отличия. Для наглядности постройте Точечную диаграмму продажи для фактических и прогнозных данных. После соответствующей корректировки она может иметь следующий вид (рис. 3.10).
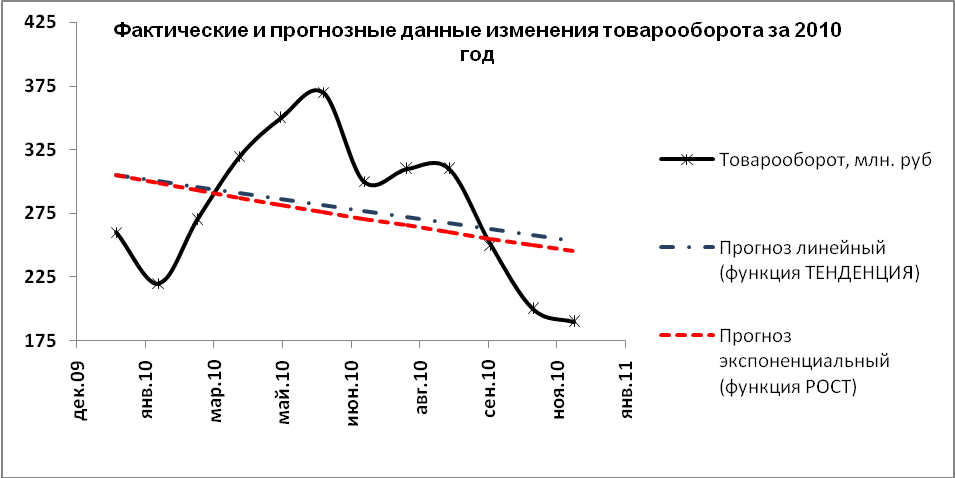
Рис. 3. 10.. Сравнение результатов фактического товарооборота магазина за 2010 год и рассчитанных по функциям ТЕНДЕНЦИЯ() и РОСТ()
Из графика видно, что применять функции ТЕНДЕНЦИЯ() и РОСТ() надо достаточно осторожно, так как они хорошо описывают только линейные процессы.
Самостоятельно вычислите среднее значение СРЗНАЧ в ячейках C15, D15 и Е15. Окно ввода аргументов функции для ячейки С15 приведено на рис. 3.11, а полученные значения – на рис. 3.14

Рис. 3. 11. Окно функции СРЗНАЧ для расчета среднего значения результатов, полученных в блоке ячеек D2:D14
