3. Используя Пакет анализа, выполните сглаживание значений ряда наблюдений y1 методами Скользящего среднего и Экспоненциального сглаживания (как в задании 1.3).
Аналогично тому, как это было уже сделано вами в задании 1.3, выполните сглаживание значений ряда наблюдений Y1 методами Скользящего среднего и Экспоненциального сглаживания.
Результат приведен на рис. 2.34 и 2.40.
4. Для исследования временных изменений ряда наблюдений, например, сезонных, выполните следующие действия:
Несколько изменим полученное уравнение линии тренда, заменив коэффициенты уравнения, на неизвестные величины «A» и «B» и добавив член с периодической компонентой, например, - С*Sin(X). Оно примет следующий вид:
Y =A + B*X+ C*Sin(X) (2.9)
где Х номер наблюдения.
В ячейках H2:J2 разместите названия коэффициентов уравнения A,B и C, а в ячейках H3:J3 их значения (которые позднее будут найдены с помощью процедуры «Поиск решения»). Для первого расчета вы можете задать их равными единице.
В ячейку D3 (столбец Y2) запишите уравнение, в котором вы намерены аппроксимировать данные наблюдений:
Например, такое
(2.10)
где $F$3, $G$3 и $H$3 - коэффициенты уравнения.
А3 - номер наблюдения (независимая переменная).
Скопируйте формулу в ячейки D4:D38.
В ячейку G3 запишите формулу квадрата разности наблюденного и предсказанного с помощью формулы значения: (C3-D3)^25 и скопируйте ее в ячейки интервала E4:E38.
В ячейке Е39 вычислите сумму квадратов отклонений =СУММ(Е3:Е38)6
Внимание. Величина суммы квадратов отклонений значений ряда наблюдений и ряда прогноза (ячейка M2) может быть также определена с помощью функции Excel (категория «Математические»)
(2.11)
Таким образом, вы подготовили наш рабочий лист к использованию программы "Поиск решения".
Для того, чтобы получить оптимальное (наилучшее) приближение к нашей функции необходимо найти минимальное значение целевой функции ячейки G39 {=СУММ (Е3:E38)} / min, (или ячейки M2 {=СУММКВРАЗН(C3:C38;D3:D38) / min}) изменяя значения коэффициентов - ячейки A, B, C (H3:J3).
Внимание. Обратите внимание, что записанная нами функция аппроксимации содержит нелинейный член (Sin(X)). Функции такого типа могут иметь не одно, а несколько решений, различающихся своими значениями7. Для решения подобных задач, необходимо указать область решения.
Это может быть сделано, задавая различные ограничения в диалоговом окне «Поиск решения». Однако, это достаточно сложная и трудоемкая задача определения граничных условий решения.
Найти необходимую область решения задачи можно, следуя следующему алгоритму:
Введите в построенную диаграмму данные уравнения прогноза. В нашем случае это ячейки D3:D38.
Для этого:
Выделите диаграмму.
Выделите команду Диаграмма / Добавить данные.
В открывшееся диалоговое окно Новые данные (рис. 2.35) введите диапазон ячеек $D$2:$D$38.
Рис. 2. 38. Добавление новых данных в диаграмму
Так как ячейки коэффициентов уравнения H3:J3 пока равны единице, вы увидите на диаграмме линию значительно ниже фактического товарооборота.
В ячейки H3 и I3 введите ранее полученные коэффициенты уравнения линии тренда (37,374 и 1,67, соответственно).
В результате выполненных действий на диаграмме появится новая линия уравнения прогноза, полностью совпадающая с ранее построенной линией тренда.
В ячейку H3 введите произвольное число (например, 10).
Рис. 2. 39. Вид диаграммы после добавления периодической составляющей
В результате к введенным данным будет добавлена периодическая компонента (подобно тому, как это показано на рис. 2.36).
Внимание. Внимательно проанализируйте ход этой периодической компоненты и при необходимости откорректируйте уравнение аппроксимации (может потребоваться изменить фазу колебаний или добавить какую-то новую компоненту и сменить тип уравнения).
В том случае, если характер новой линии аппроксимации вас устраивает, можно перейти к процедуре «Поиск решения»
Выполните команду Сервис / Поиск решения.
В открывшемся диалоговом окне выполните необходимые установки:
В окне "Установить целевую ячейку: (рис. 2.37) введите адрес целевой функции - $G$39
Переключатель Равной установите минимальному значению.
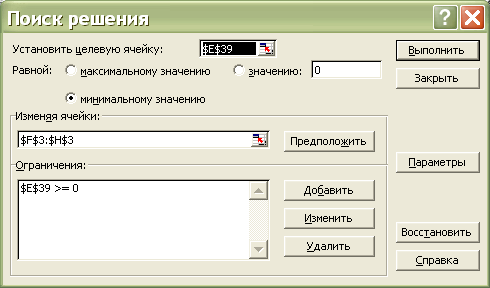
Рис. 2. 40. Диалоговое окно процедуры Поиск решения
В окне "Изменяя ячейки" укажите адреса изменяемых ячеек (коэффициентов уравнения) - $H$3:$J$3.
В окне "Ограничения" (рис. 2.38) укажите, что значение ячейки $G$39 должно быть больше нуля.
Рис. 2. 41. Диалоговое окно Изменение ограничений процедуры Поиск решения
Сохраните найденное решение, щелкнув по кнопке "ОК" (рис. 2.39).
Рис. 2. 42. Диалоговое окно Результаты поиска решений процедуры Поиск решения
В результате выполненных действий процедура "Поиск решения" определила значения коэффициентов уравнения, которое наилучшим образом аппроксимирует данные наблюдений с учетом их периодической составляющей:
(2.12)
Полученное уравнение имеет не только более высокую степень аппроксимации (см. рис. 2.34 B 2.40), но и позволяет проанализировать влияние периодической составляющей. (В нашем примере, частичное увеличение спроса ожидается в осенние месяцы).
Дальнейший анализ влияния периодической составляющей на величину объема продаж может быть направлен на оценку величины увеличения (уменьшения) объемов продаж, вызванной этой компонентой. Проведение такого анализа не вызывает особых затруднений и может быть легко выполнено вами самостоятельно.
Добавьте в диаграмму линии, полученные при определении Скользящего среднего и Экспоненциального сглаживания.
Результат приведен на рис 2.40.
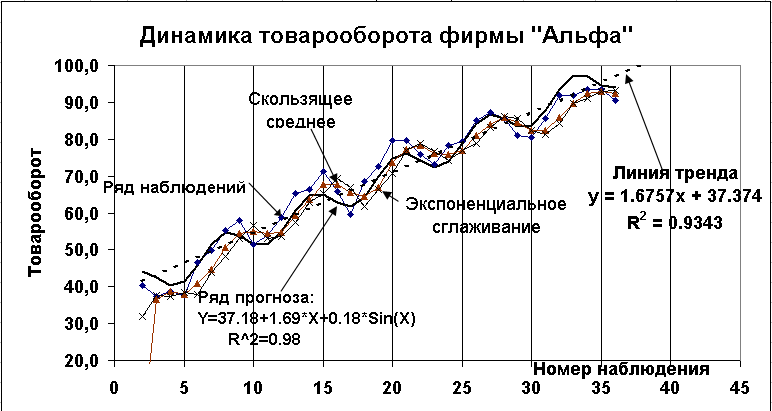
Рис. 2. 43. Пять графиков к Заданию 1.4
Внимание. Не удаляйте полученную таблицу, она вам еще пригодится.