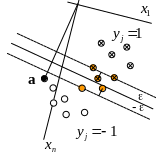
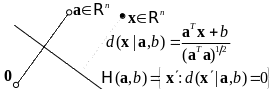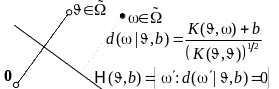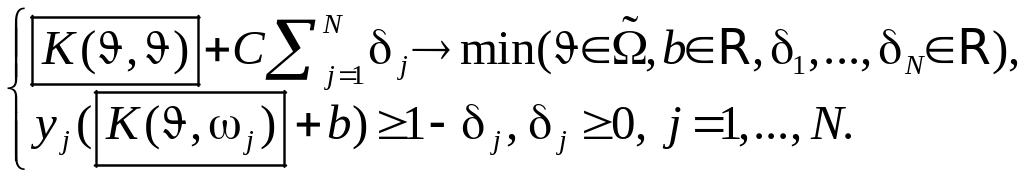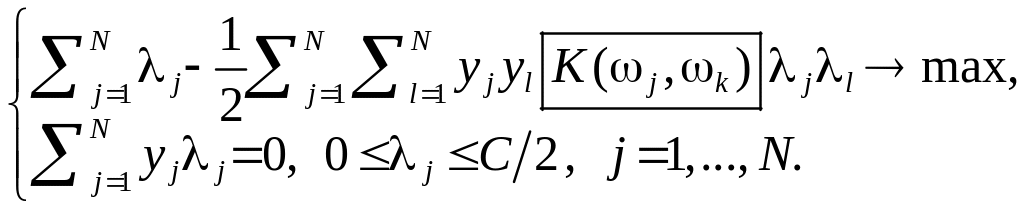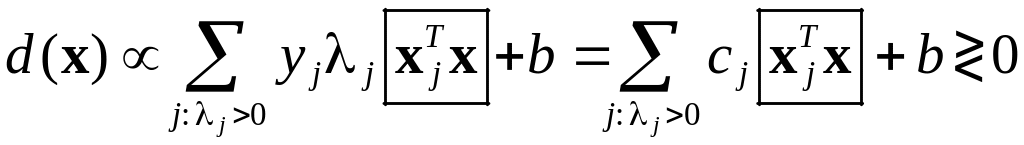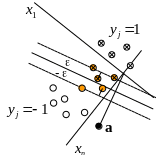- •Типовая задача восстановления закономерностей в множествах объектов реального мира
- •Концептуальная база восстановления зависимостей: гипотеза компактности
- •Диполь в метрическом пространстве
- •Простейшая реализация гипотезы компактности
- •Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
- •Идеальные условия для реализации гипотезы компактности: Евклидова метрика в конечномерном линейном пространстве
- •Метод опорных векторов: Выпуклая форма критерия
- •Метод опорных векторов: Выпуклая форма критерия
- •Метод опорных векторов: Выпуклая форма критерия
- •Повтор: Диполь в метрическом пространстве
- •Простейшая реализация гипотезы компактности
- •Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
- •Оптимальная эластичная деформация растров пары изображений
- •Среднее арифметическое изображение
- •Среднее арифметическое изображение
- •Евклидовы метрики
- •Евклидовы метрики
- •Евклидовы метрики
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Линейные операции в евклидовом метрическом пространстве
- •Потенциальная функция (кернел) на множестве объектов, определяемая евклидовой метрикой
- •Евклидова метрика на множестве объектов, определяемая потенциальной функцией (кернелом)
- •Линейный принцип восстановления зависимостей на основе потенциальной функции (Kernel-based Dependence Estimation)
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения для произвольной функции попарного сравнения объектов: Relational Dependence Estimation
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Relevance Object Machine – выпуклый критерий обучения в линейном пространстве вторичных признаков
- •Более общая концепция: Несколько разных функций парного сравнения объектов
- •Более общая концепция: Несколько разных функций парного сравнения объектов
- •Типичная зависимость ошибки на контроле и числа релевантных объектов от уровня селективности вторичных признаков
- •Частный случай: Метрика как функция попарного сравнительного представления объектов
- •Р егуляризованный критерий обучения в метрическом пространстве объектов
Линейные операции в евклидовом метрическом пространстве
Произвольный выбор
центра метрического пространства
![]() .
.
Умножение
элемента
|
Сложение элементов
|
|
|
|
|
Скалярное произведение двух элементов (потенциальная функция, кернел) |
|
- Сложение коммутативно и ассоциативно ;
- существует нулевой элемент , ;
- для каждого элемента существует обратный ему элемент ;
- умножение ассоциативно ;
- умножение на единицу оставляет элемент без изменения ;
- сложение и умножение дистрибутивны , ;
- скалярное
произведение линейно,
![]() ;
;
-
![]()
![]() ,
причем
,
причем
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() ;
;
-
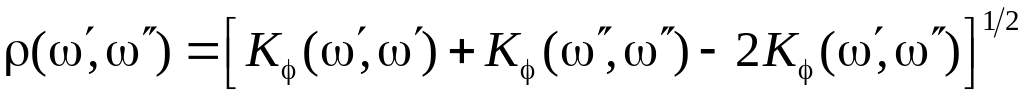 .
.
Потенциальная функция (кернел) на множестве объектов, определяемая евклидовой метрикой
Множество объектов реального мира
![]()
евклидова метрика
![]() :
:
условно положительно определенные матрицы
пополнение
метрического пространства
всеми соосными элементами
![]() и продолжение евклидовой метрики
и продолжение евклидовой метрики
выбор центра
линейные операции
в
![]() с нулевым элементом
и скалярным произведением
с нулевым элементом
и скалярным произведением
![]() – полож. опред.
матрицы
– полож. опред.
матрицы
![]()
преобразование
кернела при изменении центра
![]()
![]()
Евклидова метрика
в
порождает класс линейных пространств
с разными нулевыми элементами, разными
линейными операциями, разными скалярными
произведениями, но с одной и той же
евклидовой метрикой
.
Евклидова метрика на множестве объектов, определяемая потенциальной функцией (кернелом)
Множество объектов реального мира
кернел
![]() :
:
положительно
определенные матрицы
![]()
евклидова метрика
– условно полож. опр. матрицы
![]()
пополнение метрического пространства всеми соосными элементами и продолжение евклидовой метрики
центр автоматически
определен как
:
![]()
линейные
операции в
с нулевым элементом
![]() и скалярным произведением
и скалярным произведением
![]()
преобразование
кернела при изменении центра
![]()
Класс эквивалентных
кернелов в
порождает класс линейных пространств
с разными нулевыми элементами, разными
линейными операциями, разными скалярными
произведениями, но с одной и той же
евклидовой метрикой
.
Линейный принцип восстановления зависимостей на основе потенциальной функции (Kernel-based Dependence Estimation)
Объекты
|
Объекты
.
Линейный принцип в
|
Распознавание объектов двух классов, метод опорных векторов |
|
Критерий обучения в :
|
Критерий обучения в :
|
Двойственная задача:
|
Двойственная задача:
|
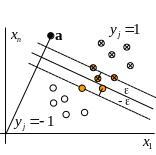
Правило классификации нового объекта:
|
Правило классификации нового объекта:
|
Напомним: Существует континуум линейных пространств и кернелов, выражающих одну и ту же евклидову метрику, различающихся лишь выбором нулевого элемента. |
|
Правило классификации
нового объекта, полученное по обучающей
совокупности, определяется только
взаимными евклидовыми расстояниями
между объектами обучающей совокупности
![]()
В частности, в :
|
|
В линейном пространстве , определяемом кернелом:
![]()
Правило классификации нового объекта:

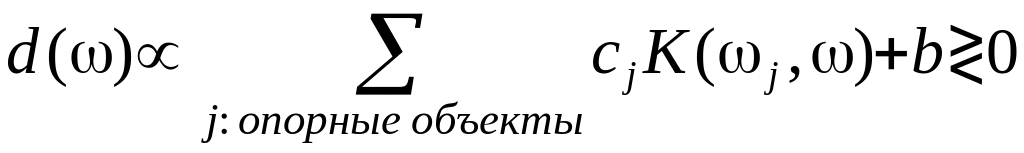
При переносе нуля
линейного пространства коэффициенты
![]() ,
определяющие расстояние объекта от
метрической гиперплоскости, будут
изменяться, но состав множества опорных
объектов и само значение расстояния
остается неизменным.
,
определяющие расстояние объекта от
метрической гиперплоскости, будут
изменяться, но состав множества опорных
объектов и само значение расстояния
остается неизменным.
Как обойтись без
выбора нулевого элемента при погружении
множества объектов с евклидовой метрикой
в линейное пространство?
Как обеспечить
возможность интерполяции непосредственно
между элементами евклидова метрического
пространства при выборе метрической
гиперплоскости?
Аффинные операции в евклидовом метрическом пространстве
Пусть – множество объектов реального мира с евклидовой метрикой :
![]() ,
если
,
если
![]() .
.
Аффинные операции в евклидовом метрическом пространстве
Пусть – множество объектов реального мира с евклидовой метрикой :
, если .
Пусть – евклидово метрическое пространство, являющееся его неограниченным выпуклым замыканием.
Аффинные операции в евклидовом метрическом пространстве
Пусть – множество объектов реального мира с евклидовой метрикой :
, если .
Пусть – евклидово метрическое пространство, являющееся его неограниченным выпуклым замыканием.
Напомним, что
евклидово
метрическое пространство
вместе с любой парой его элементов
содержит также и всю определяемую ими
ось
![]() .
.
Аффинные операции в евклидовом метрическом пространстве
Пусть – множество объектов реального мира с евклидовой метрикой :
, если .
Пусть – евклидово метрическое пространство, являющееся его неограниченным выпуклым замыканием.
Напомним, что евклидово метрическое пространство вместе с любой парой его элементов содержит также и всю определяемую ими ось .
Обобщим понятие
соосности на произвольную конечную
неупорядоченную совокупность элементов
евклидова метрического пространства
![]() .
.
Пусть
![]() – числовой вектор, такой что условию
– числовой вектор, такой что условию
![]() ,
т.е.
,
т.е.
![]() .
.
Р
![]()
![]()
![]() ,
,
![]() .
.