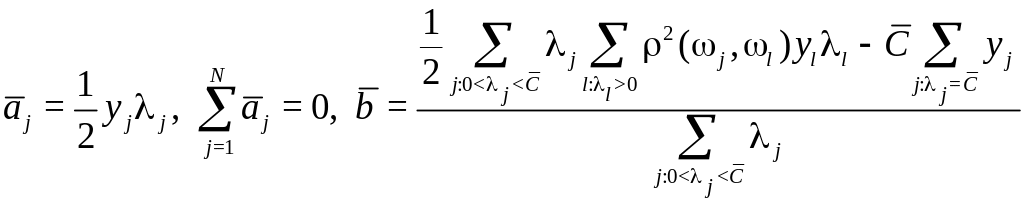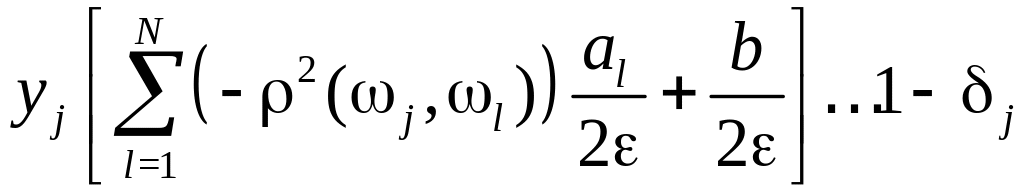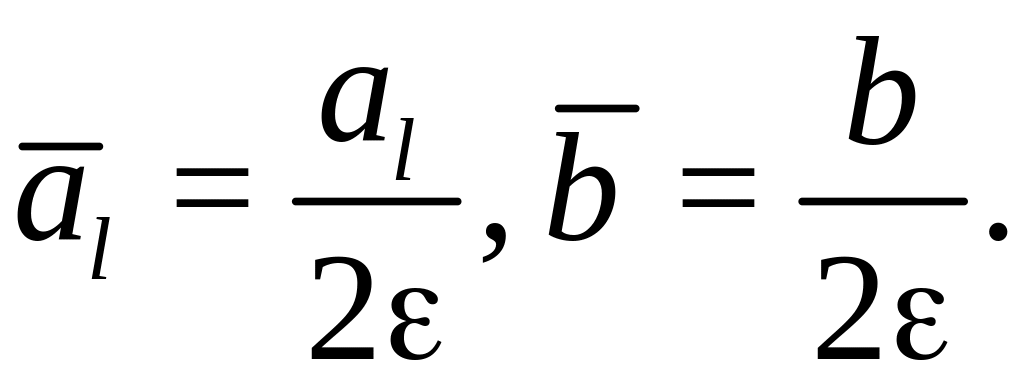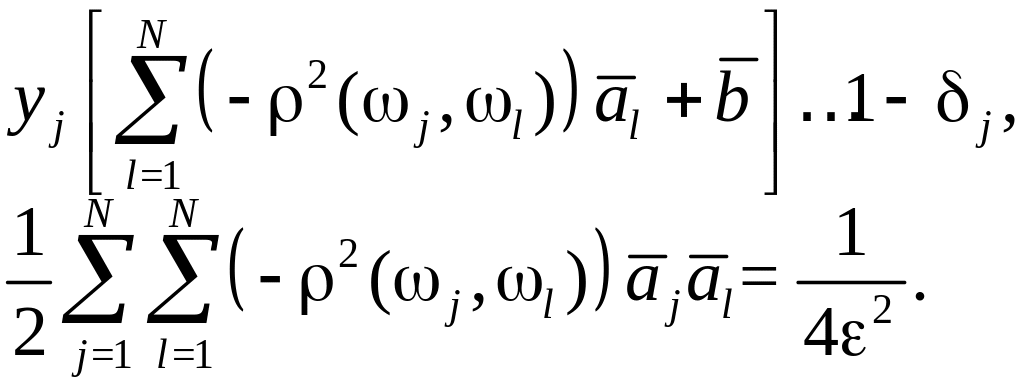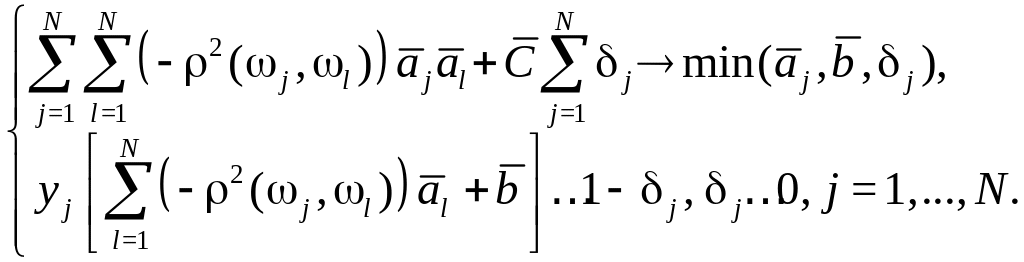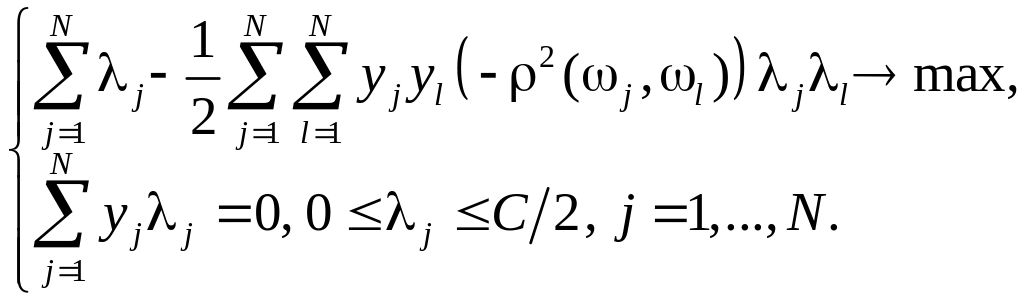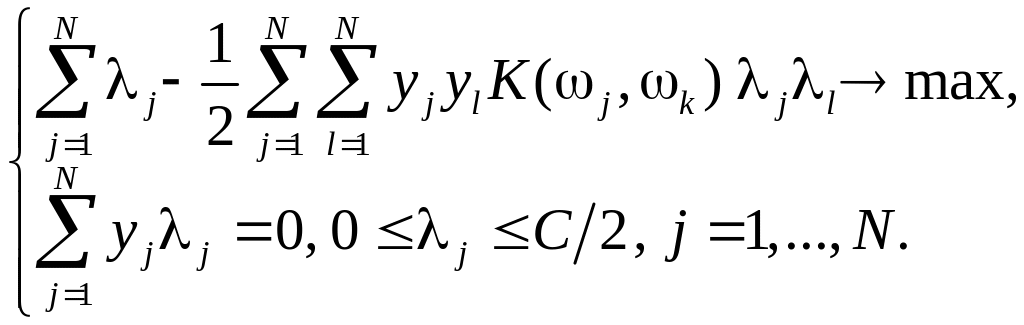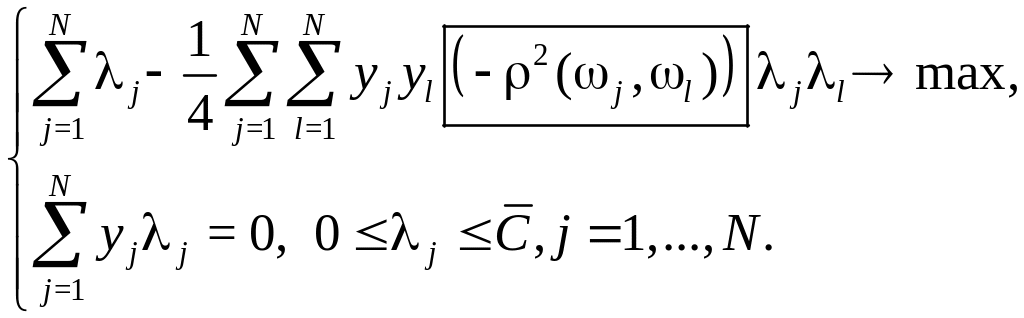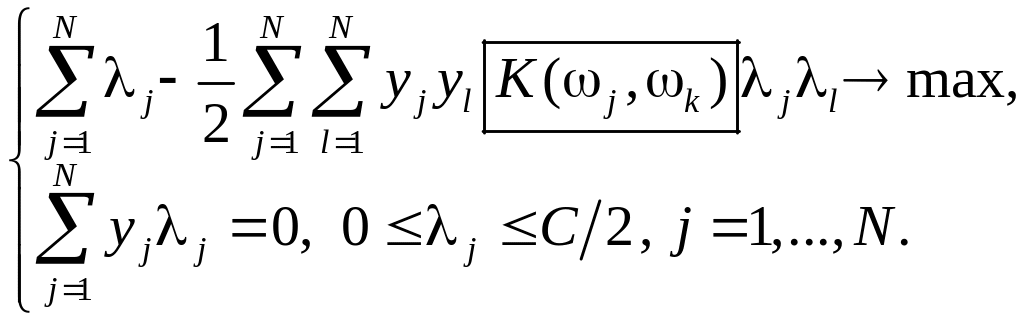- •Типовая задача восстановления закономерностей в множествах объектов реального мира
- •Концептуальная база восстановления зависимостей: гипотеза компактности
- •Диполь в метрическом пространстве
- •Простейшая реализация гипотезы компактности
- •Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
- •Идеальные условия для реализации гипотезы компактности: Евклидова метрика в конечномерном линейном пространстве
- •Метод опорных векторов: Выпуклая форма критерия
- •Метод опорных векторов: Выпуклая форма критерия
- •Метод опорных векторов: Выпуклая форма критерия
- •Повтор: Диполь в метрическом пространстве
- •Простейшая реализация гипотезы компактности
- •Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
- •Оптимальная эластичная деформация растров пары изображений
- •Среднее арифметическое изображение
- •Среднее арифметическое изображение
- •Евклидовы метрики
- •Евклидовы метрики
- •Евклидовы метрики
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Линейные операции в евклидовом метрическом пространстве
- •Потенциальная функция (кернел) на множестве объектов, определяемая евклидовой метрикой
- •Евклидова метрика на множестве объектов, определяемая потенциальной функцией (кернелом)
- •Линейный принцип восстановления зависимостей на основе потенциальной функции (Kernel-based Dependence Estimation)
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения для произвольной функции попарного сравнения объектов: Relational Dependence Estimation
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Relevance Object Machine – выпуклый критерий обучения в линейном пространстве вторичных признаков
- •Более общая концепция: Несколько разных функций парного сравнения объектов
- •Более общая концепция: Несколько разных функций парного сравнения объектов
- •Типичная зависимость ошибки на контроле и числа релевантных объектов от уровня селективности вторичных признаков
- •Частный случай: Метрика как функция попарного сравнительного представления объектов
- •Р егуляризованный критерий обучения в метрическом пространстве объектов
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
|
Представление искомых узлов диполя: , , . |
В условиях принятых предположений достаточно искать дискриминантную функцию в виде |
|
Эквивалентная формулировка задачи:
|
Здесь не учтены
ограничения на коэффициенты при
объектах обучающей совокупности
|
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
Эквивалентная формулировка задачи:
|
Это задача квадратичного программирования |
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
Эквивалентная формулировка задачи:
|
Это задача квадратичного программирования |
Разделим обе части
ограничений-неравенств во второй строке
на
![]() :
:
|
Замена переменных:
|
|
|
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
Эквивалентная формулировка задачи:
|
Это задача квадратичного программирования |
Разделим обе части ограничений-неравенств во второй строке на :
|
Замена переменных: |
Ограничения:
|
Эквивалентная
формулировка задачи
|
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
Эквивалентная формулировка задачи:
|
Это задача квадратичного программирования |
Разделим обе части ограничений-неравенств во второй строке на :
|
Замена переменных: |
Ограничения:
|
Эквивалентная
формулировка задачи
|
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
Эквивалентная формулировка задачи:
|
Это задача квадратичного программирования |
Двойственная задача:
|
Для сравнения: двойственная задача Kernel-based SVM
|
Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
Обучающая совокупность: |
|
Эквивалентная формулировка задачи:
|
Это задача квадратичного программирования
|
Двойственная задача:
|
Для сравнения: двойственная задача Kernel-based SVM
|
Решение: