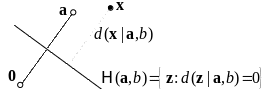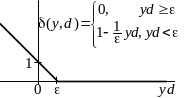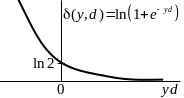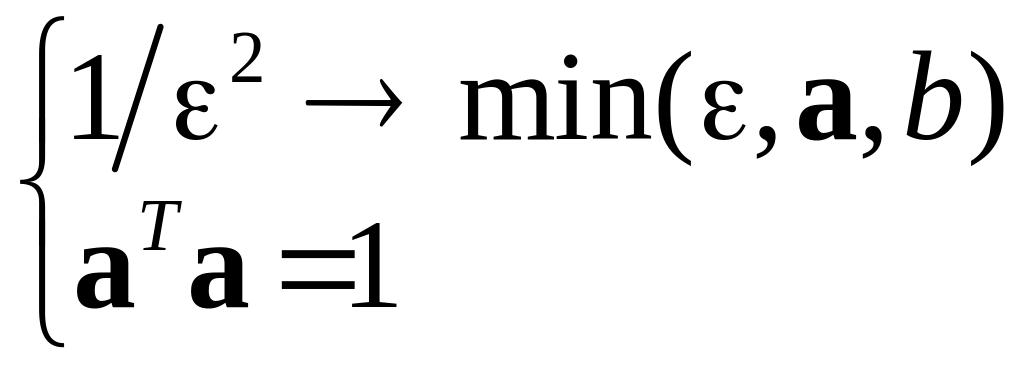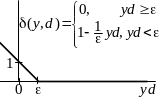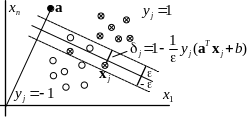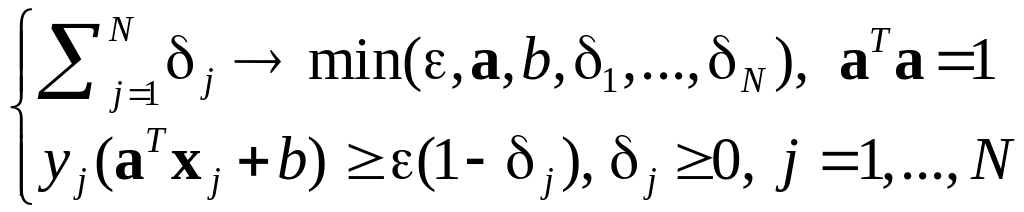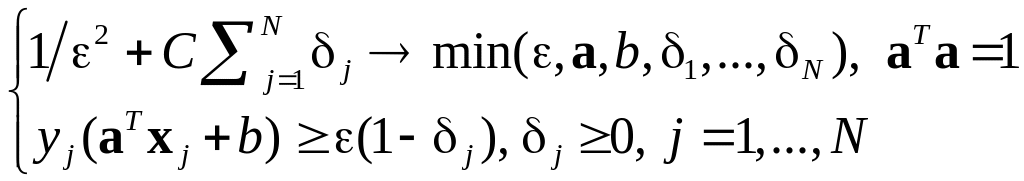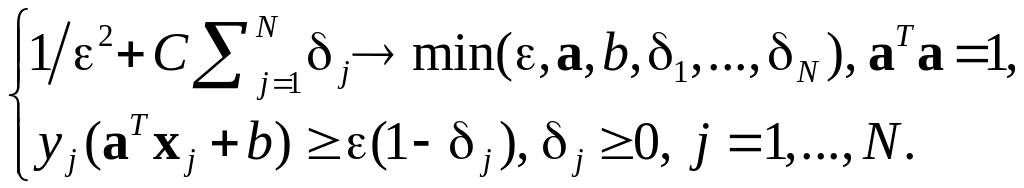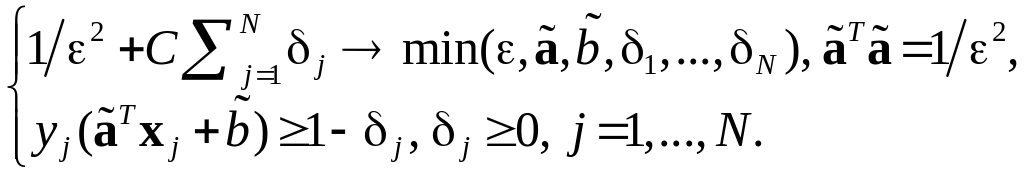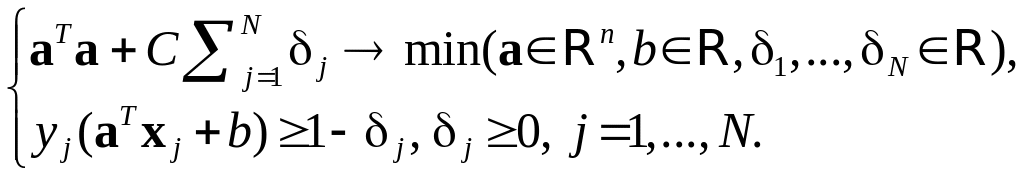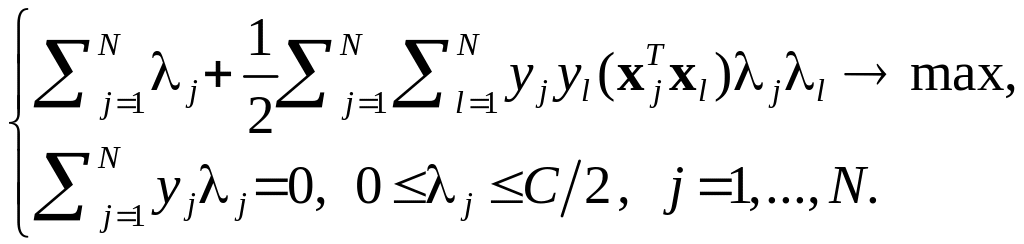- •Типовая задача восстановления закономерностей в множествах объектов реального мира
- •Концептуальная база восстановления зависимостей: гипотеза компактности
- •Диполь в метрическом пространстве
- •Простейшая реализация гипотезы компактности
- •Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
- •Идеальные условия для реализации гипотезы компактности: Евклидова метрика в конечномерном линейном пространстве
- •Метод опорных векторов: Выпуклая форма критерия
- •Метод опорных векторов: Выпуклая форма критерия
- •Метод опорных векторов: Выпуклая форма критерия
- •Повтор: Диполь в метрическом пространстве
- •Простейшая реализация гипотезы компактности
- •Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
- •Оптимальная эластичная деформация растров пары изображений
- •Среднее арифметическое изображение
- •Среднее арифметическое изображение
- •Евклидовы метрики
- •Евклидовы метрики
- •Евклидовы метрики
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Пополнение метрического пространства с евклидовой метрикой
- •Линейные операции в евклидовом метрическом пространстве
- •Потенциальная функция (кернел) на множестве объектов, определяемая евклидовой метрикой
- •Евклидова метрика на множестве объектов, определяемая потенциальной функцией (кернелом)
- •Линейный принцип восстановления зависимостей на основе потенциальной функции (Kernel-based Dependence Estimation)
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Аффинные операции в евклидовом метрическом пространстве
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Евклидово аффинное пространство
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения распознаванию объектов двух классов: Принцип максимизации зазора (аналог задачи svm)
- •Задача обучения для произвольной функции попарного сравнения объектов: Relational Dependence Estimation
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
- •Relevance Object Machine – выпуклый критерий обучения в линейном пространстве вторичных признаков
- •Более общая концепция: Несколько разных функций парного сравнения объектов
- •Более общая концепция: Несколько разных функций парного сравнения объектов
- •Типичная зависимость ошибки на контроле и числа релевантных объектов от уровня селективности вторичных признаков
- •Частный случай: Метрика как функция попарного сравнительного представления объектов
- •Р егуляризованный критерий обучения в метрическом пространстве объектов
Линейные методы восстановления зависимостей по эмпирическим данным
В.В. Моттль
Вычислительный центр РАН
Московский физико-технический институт
О.С. Середин
Тульский государственный университет
Типовая задача восстановления закономерностей в множествах объектов реального мира
Некоторое множество
реально существующих объектов
![]() .
.
Некоторое
множество значений скрытой характеристики
объектов
![]() .
.
Объективно
существующая скрытая функция
![]() .
.
Желание наблюдателя:
Иметь инструмент оценивания скрытой характеристики для реальных объектов
![]() ;
;
![]() – ошибка.
– ошибка.
Обучение по прецедентам:
Подмножество
наблюдаемых объектов, для которых
измерено значение функции
![]() ,
,
![]() .
.
Задача:
Продолжить
функцию на все множество
![]() ,
так чтобы можно было в дальнейшем
оценивать значение рассматриваемой
характеристики
,
так чтобы можно было в дальнейшем
оценивать значение рассматриваемой
характеристики
![]() для новых объектов
для новых объектов
![]() .
.
Типовая задача восстановления закономерностей в множествах объектов реального мира
Некоторое множество реально существующих объектов .
Некоторое множество значений скрытой характеристики объектов .
Объективно существующая скрытая функция .
Желание наблюдателя:
Иметь инструмент оценивания скрытой характеристики для реальных объектов
; – ошибка.
Простейшие случаи:
Задача
распознавания образов
![]() – конечное неупорядоченное множество;
в частности
– конечное неупорядоченное множество;
в частности
![]() .
.
Задача
восстановления числовой функции
![]() – множество действительных чисел.
– множество действительных чисел.
Концептуальная база восстановления зависимостей: гипотеза компактности
Множество объектов реального мира Скрытая характеристика объекта (целевая характеристика) Искомое решающее правило |
|
Основная идея:
Выбрать в множестве объектов некоторую метрику
![]()
![]() ,
,
![]() ,
если
,
если
![]() ,
,
![]()
Принимать
для близких объектов
![]() близкие решения
близкие решения
![]() в задаче
распознавания образов
в задаче
распознавания образов
![]() в задаче восстановления
числовой зависимости
в задаче восстановления
числовой зависимости
Выбор метрик удачен, если для них выполняется гипотеза компактности
(Эммануил Маркович Браверман, 1961):
Для пар объектов
![]() ,
похожих в смысле выбранной метрики
,
,
похожих в смысле выбранной метрики
,
значения целевой
характеристики также в большинстве
случаев близки
![]() .
.
Диполь в метрическом пространстве
Метрическое
пространство объектов реального мира:
,
![]() – метрика
– метрика
Диполь в метрическом
пространстве – упорядоченная пара:
![]()
Простейшая реализация гипотезы компактности
Принадлежность произвольного объекта к одному из двух классов
|
В
множестве объектов
слишком мало элементов.
К тому же,
наблюдатель располагает лишь конечной
обучающей совокупностью объектов
|
Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства
![]() – воображаемое
непрерывное метрическое пространство,
в котором множество реальных объектов
является подмножеством, быть может,
изолированных элементов.
– воображаемое
непрерывное метрическое пространство,
в котором множество реальных объектов
является подмножеством, быть может,
изолированных элементов.
![]() ,
,
![]() – метрическая гиперплоскость в
– метрическая гиперплоскость в
![]()
![]()

 – проекция реального
объекта
– проекция реального
объекта
![]() на гиперплоскость в
на гиперплоскость в
Р |
|
|
Классификация:
Числовая
зависимость:
|
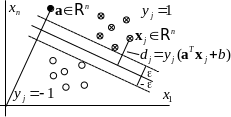
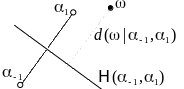
Идеальные условия для реализации гипотезы компактности: Евклидова метрика в конечномерном линейном пространстве
Вектор
действительных признаков
![]() погружает множество реальных объектов
в
погружает множество реальных объектов
в
![]()
Естественная евклидова метрика в
Диполь:
![]() ,
,
![]() ;
;
![]() – направляющий вектор гиперплоскости
– направляющий вектор гиперплоскости
Смещенная
гиперплоскость, определяемая диполем:
![]() ,
,
![]()
Решающая
функция – decision
(score)
function:
Расстояние
от точки
|
|
Ф
Двухклассовое
распознавание: Метод опорных векторов
Двухклассовое
распознавание: Метод логистической
регрессии
Линейная модель
числовой зависимости с квадратичной
функцией потерь
Индекс класса
объекта
|
||
|
Метод опорных
векторов
|
|
Метод опорных векторов (Support Vector Machine – SVM): Принцип максимального зазора (margin) между классами
Обучающая
совокупность
![]() ,
,
![]() ,
,
![]()
|
Требование максимизации зазора между линейно разделимыми классами
|
|
|
Требование минимизации суммы штрафов
|
|
Компромисс:
|
Оптимизация на
сфере
|
Метод опорных векторов: Выпуклая форма критерия
Невыпуклый критерий |
Замена переменных |
|
|
Результат замены: |
|
Выпуклый критерий обучения: Задача квадратичного программирования
|
|
Метод опорных векторов: Выпуклая форма критерия
Выпуклый критерий обучения: Задача квадратичного программирования переменных, ограничений |
|
|
|
Двойственная форма задачи: Задача квадратичного программирования П
опорные векторы
|
|
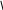
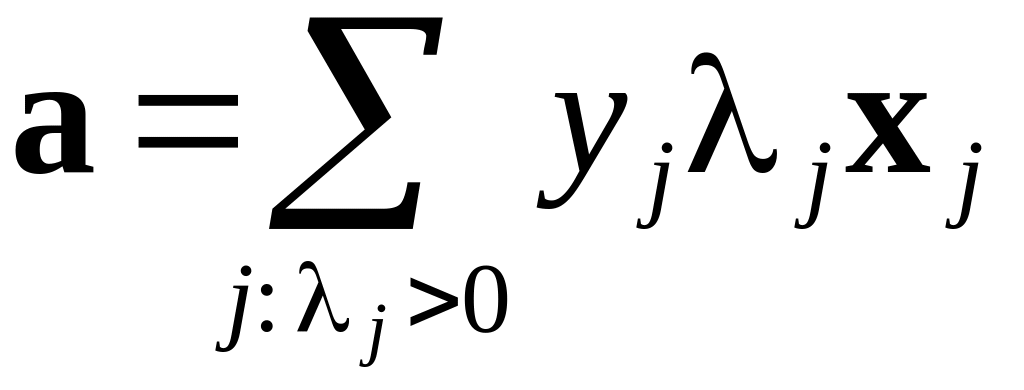 ,
,
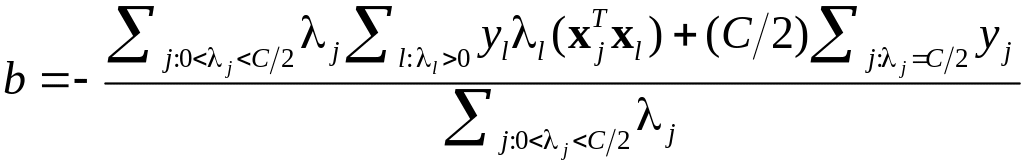 ,
,
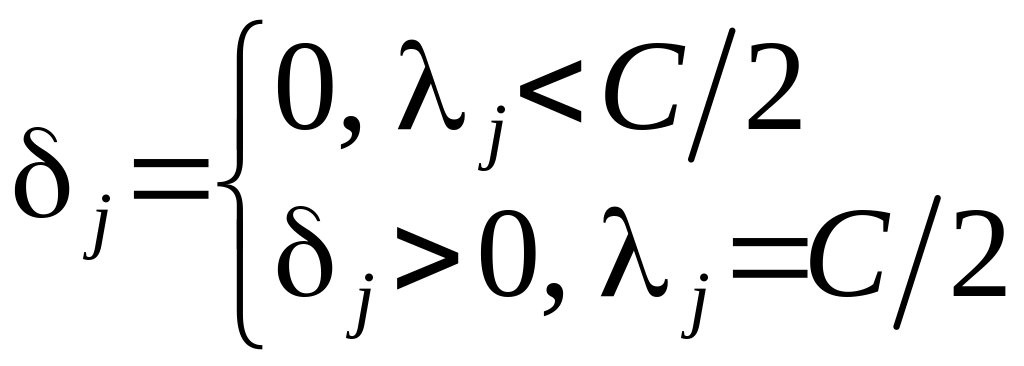
Правило классификации
нового объекта
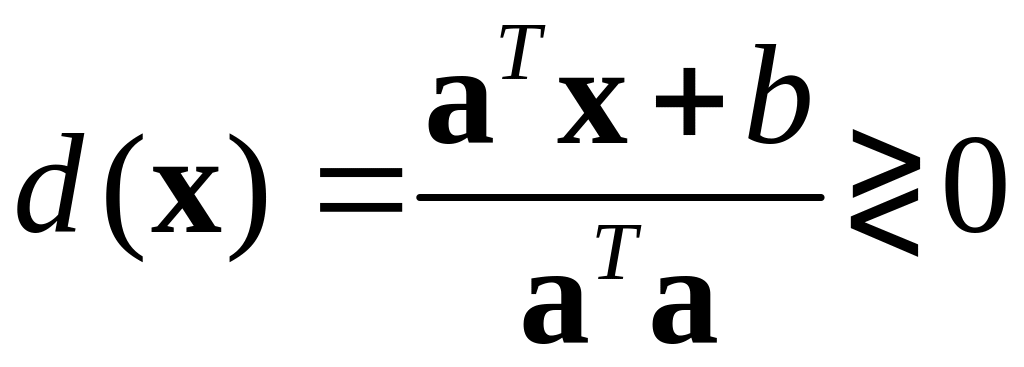
Эквивалентная
запись
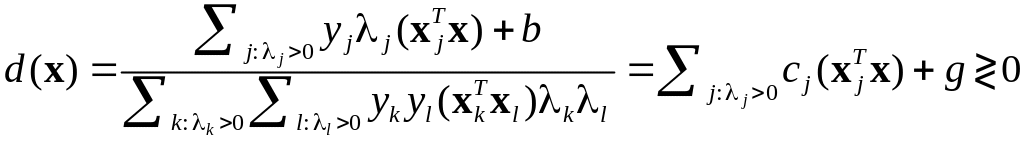

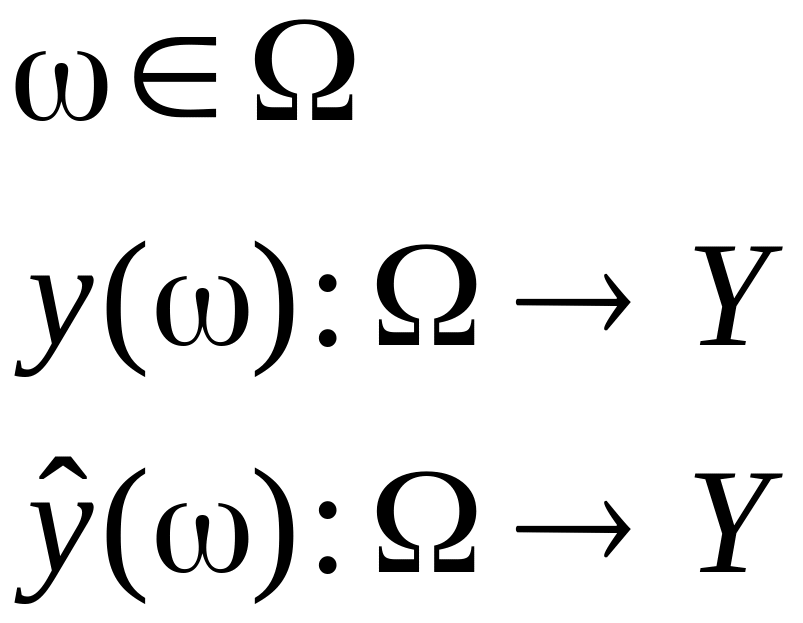
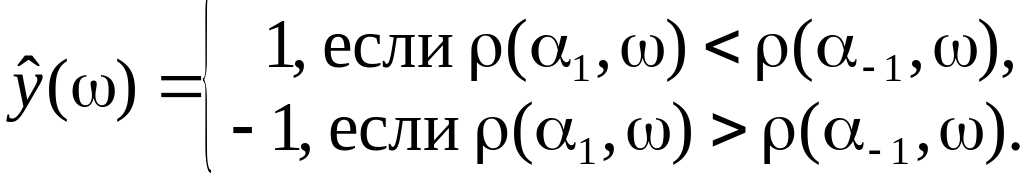 Как
выбрать диполь?
Как
выбрать диполь?
 ешающая
функция (score
function):
расстояние точки от
гиперплоскости
в
с учетом знака
ешающая
функция (score
function):
расстояние точки от
гиперплоскости
в
с учетом знака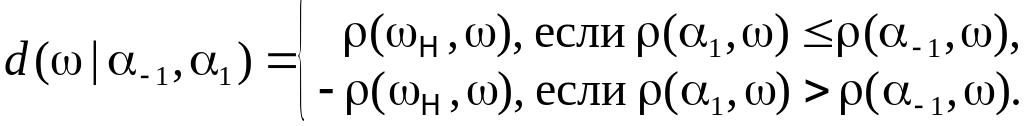
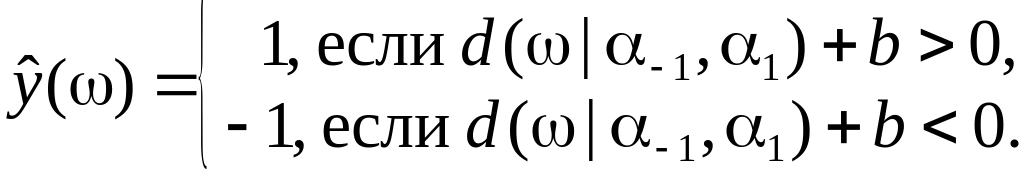
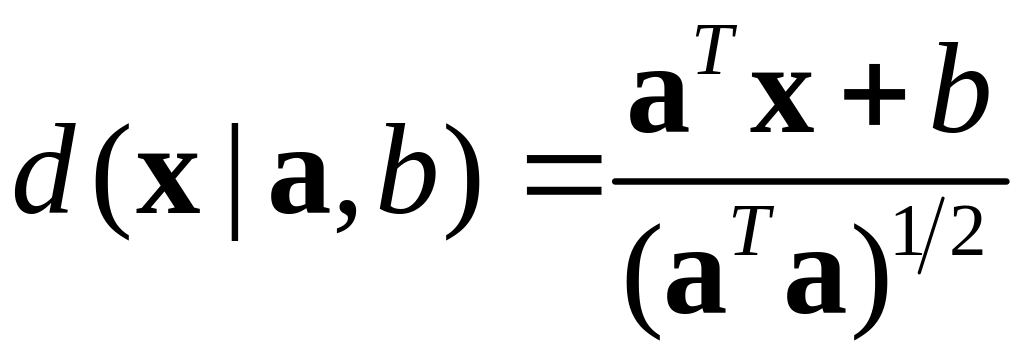 ,
,