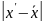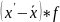Задание 3.
Определить дисперсию производственного стажа рабочих в каждом цехе и по заводу в целом; среднюю из цеховых дисперсий; межцеховую дисперсию. Объяснить смысл дисперсий. Используя их, проверить правило сложения дисперсий.
Дисперсия представляет собой среднюю арифметическую из квадратов отклонений вариант от их средней арифметической и характеризует вариацию признака за счёт всех других признаков действующих внутри совокупности.
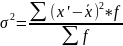
Таблица 3 – Распределение рабочих цеха №1 по стажу
Стаж |
|
f |
x'*f |
|
|
|
До 1 |
5 |
0,5 |
2,50 |
4,51 |
22,56 |
101,81 |
1-2 |
8 |
1,5 |
12,00 |
3,51 |
28,10 |
98,70 |
3-5 |
12 |
4 |
48,00 |
1,01 |
12,15 |
12,30 |
6-10 |
11 |
8 |
88,00 |
2,99 |
32,86 |
98,18 |
Свыше 10 |
4 |
12,5 |
50,00 |
7,49 |
29,95 |
224,25 |
Итого |
40 |
|
200,5 |
|
125,63 |
535,24 |

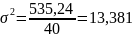

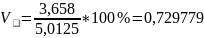
Таблица 4 – Распределение рабочих цеха №2 по стажу
Стаж |
|
f |
x'*f |
|
|
|
До 1 |
5 |
0,50 |
2,50 |
5,66 |
28,29 |
160,08 |
1-2 |
11 |
1,50 |
16,50 |
4,66 |
51,24 |
238,70 |
3-5 |
15 |
4,00 |
60,00 |
2,16 |
32,38 |
69,88 |
6-10 |
16 |
8,00 |
128,00 |
1,84 |
29,47 |
54,27 |
Свыше 10 |
13 |
12,50 |
162,50 |
6,34 |
82,44 |
522,82 |
Итого |
60 |
|
369,50 |
|
223,82 |
1045,75 |

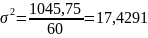
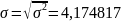

Таблица 5 – Распределение рабочих завода по стажу
Стаж |
|
f |
x'*f |
|
|
|
До 1 |
10 |
0,50 |
5,00 |
5,20 |
5,20 |
52,00 |
1-2 |
19 |
1,50 |
28,50 |
4,20 |
4,20 |
79,80 |
3-5 |
27 |
4,00 |
108,00 |
1,70 |
1,70 |
45,90 |
6-10 |
27 |
8,00 |
216,00 |
2,30 |
2,30 |
62,10 |
Свыше 10 |
17 |
12,50 |
212,50 |
6,80 |
6,80 |
115,60 |
Итого |
100 |
|
570,00 |
|
355,40 |
1612,50 |
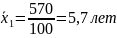
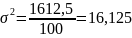
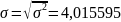
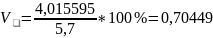
Общая
дисперсия
 )
представляет собой среднюю арифметическую
из квадратов отклонений вариант от их
средней арифметической. Она характеризует
вариацию признака за счёт всех других
признаков действующих внутри совокупности.
Дисперсия (взвешенная) определяется
следующим образом:
)
представляет собой среднюю арифметическую
из квадратов отклонений вариант от их
средней арифметической. Она характеризует
вариацию признака за счёт всех других
признаков действующих внутри совокупности.
Дисперсия (взвешенная) определяется
следующим образом:
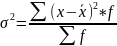

Групповая
дисперсия (
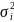 )отражает вариацию признака за счет
условий и причин, действующих внутри
группы.
)отражает вариацию признака за счет
условий и причин, действующих внутри
группы.
Средняя
из групповых дисперсий
( )
считается (данная формула используется,
так как частоты для групп не даны):
)
считается (данная формула используется,
так как частоты для групп не даны):

Межгрупповая дисперсия ) характеризует вариацию результативного признака за счет признака группировки.

Правило сложения дисперсий:

Подставим полученные значения:
16,125=15,405083+0,31509
16,125≈15,720173
Незначительная разница вызвана округлением. Правило действует.