1.6. Изображения графов на плоскости

При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов). Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются отрезком или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра. Различают планарные и непланарные графы. Планарный граф — это граф, который можно изобразить на рисунке без пересечения рёбер (простейшие — треугольник или пара связанных вершин), иначе — непланарный. В том случае, если граф не содержит циклов (путей однократного обхода рёбер и вершин с возвратом в исходную вершину), его принято называть «деревом». Важные виды деревьев в теории графов — бинарные деревья, где каждая вершина имеет одно входящее ребро и ровно два выходящих, или является конечной — не имеющей выходящих рёбер.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

1.7. Теория графов в информатике (Граф-схема алгоритма)

Рисунок 1.9.1 Граф-схема алгоритма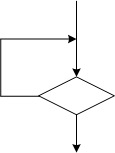

Граф-схема алгоритма (ГСА) — конечный связный ориентированный граф G=(A,V), вершины которого   соответствуют операторам, а дуги   задают порядок следования вершин (операторов) алгоритма, где   — число вершин графа,   — число дуг. В более широком смысле вершинам графа соответствуют не только операторные вершины, но и условные, начальная и конечная вершины и т.д. При рассмотрении параллельных алгоритмов вводится понятие параллельной граф-схемы алгоритма (Пар ГСА), в состав которой входят вершины распараллеливания/синхронизации, функциональность которых обычно совмещается. Иногда в состав ГСА вводятся вершины дополнительных типов: объединения альтернативных дуг (парная вершина для условной вершины), фиктивные операторные вершины, вершины маркировки (с целью обеспечения возможности моделирования выполнения алгоритма Сетью Петри), ждущие вершины.

Однако не любой ориентированный граф, составленный из вершин указанных выше типов, может быть отождествлен с корректным алгоритмом. Например, из операторной вершины не может выходить более алгоритмов обработки графов общего вида, зачастую имеют существенные отличия ввиду использования особых свойств ГСА, что позволяет их упрощение, снижение временной или емкостной сложности.

В составе граф-схемы алгоритма могут быть выделены более крупные элементы, представленные подмножествами ее вершин и дуг: ветви (линейные цепочки или участки вершин) и фрагменты (начальный, параллельный, альтернативный, циклические с пред-, постусловием и прерыванием). Эквивалентным представлением граф-схемы корректного алгоритма является древо фрагментов, отражающее порядок вложенности фрагментов

одной дуги. Поэтому на практике обычно ограничиваются рассмотрением подкласса граф-схем алгоритмов, удовлетворяющих свойствам безопасности, живости и устойчивости. Алгоритмы преобразования ГСА, являющиеся подмножеством.

2. Моей задачей было в данном проекте провести тестирование человека с помощью Теорией Графов. Для реализации данного проекта я решил написать программу с математическим, уклонам на языке программирования Pascal. Но при этом использовал программу Delphi 7 которая является расширённой версией Pascal. Польза от проделанной мной работы. Моя работа помогает развивать математическое мышление и быстродействие в ориентировании программы, которое поможет в дальнейшем ориентироваться в других программах.