Математическое описание профиля волны

Координаты волнового профиля на поверхности воды определятся известными формулами, определяющими положение вращающейся точки во времени

,

,

где амплитуда волны,

Радиусы орбит уменьшаются с увеличением глубины по следующему закону

Координаты волнового профиля с учётом изменения положения точки по высоте

Распределение давления в волне также будет периодическим и определяется формулой

,

где атмосферное давление на поверхности, аппликата рассматриваемой точки, - удельный вес воды. Таким образом, давление складывается из статического давления при невозмущённой поверхности и динамической добавки

Именно вызывает качку судна на волнении. На невозмущенной поверхности воды следовательно, волновая добавка будет равна:

Если волновое движение отсутствует,

Сумма кинетической и потенциальной энергии волн малой амплитуды постоянна и пропорциональна квадрату амплитуды волны.

.

Погонная энергия, т.е. энергия, приходящаяся на 1 м ширины волны

.

Нерегулярное волнение

Как отмечалось ранее, ветровое волнение имеет трехмерный характер, однако описание его при этом получается сложным. Поэтому на практике обычно считается, что ветровое волнение всегда двумерное (плоское). Погрешность от такого представления оказывает влияние в безопасную сторону, так как несколько увеличивает расчетные амплитуды качки, закладываемые в нормы остойчивости.

Образец записи нерегулярного волнения изображен на рис. 9.2. Наглядно видно, что каждая последующая волна отличается от предыдущей по высоте h, и периоду , т.е. фактически по длине.

При описании нерегулярного волнения амплитуда волны берется равной .

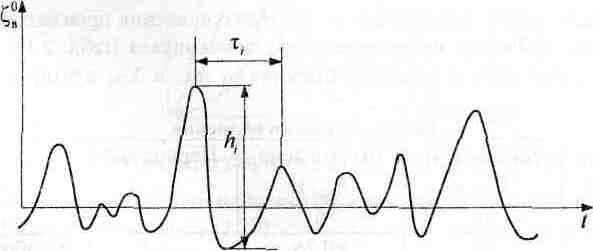
Рис. 9.2. Запись нерегулярного волнения

Существуют три метода описания нерегулярного волнения: статистический, спектральный и корреляционный. Корреляционный метод применяется чаще всего при научном анализе реализаций волнения. В практических же расчетах применяются в основном статистический и спектральный методы. Рассмотрим их более подробно.

Статистический метод.

С помощью этого метода производится оценка вероятности возникновения волн различной высоты. Определить вероятность можно приближенно, взяв довольно длинную запись волнения и сняв с нее высоты волн. Тогда вероятность возникновения волны с амплитудой , будет равна:

где - число волн с амплитудой , на записи; n - общее число волн на записи. Чем длиннее запись, тем более точно определяется вероятность.

Оценка интенсивности волнения производится с помощью дисперсии (квадрата среднего квадратичного отклонения)

Средняя высота волны (в вероятностном смысле) связана с дисперсией соотношением

На практике обычно применяется не вероятность возникновения волны какой-то высоты, а обеспеченность. Обеспеченность - это вероятность возникновения волн с высотой, большей или равной заданной.

Таким образом, трехпроцентная обеспеченность обозначает, что из 100 волн только 3 будут иметь высоту, большую или равную заданной высоте. Обеспеченность записывается в виде индекса, например , .

Средняя высота волны имеет обеспеченность 46,5%, т.е.

;

В таблицах балльности волн обычно выписываются значения , для которых

; . (2.23)

Иногда необходимо определить дисперсию волны, зная высоту Из (2.23) следует

Высота волны 0,5%-ной обеспеченности называется максимальной и описывается формулой

; (2.25)

Обобщенная оценка интенсивности ветрового волнения производится в условных единицах - баллах. В России применяется 9-балльная шкала (табл. 9.1). Связь между средними значениями , и в этой таблице определяется по формуле Циммермана.

Таблица 9.1 Таблица балльности волнения и ветра

Балльность волн	Балльность ветра	Длина волн , м	Высота волн, , м	Период волн , с	Описательная характеристика
0	0-1	0	0	0	Отсутствует
I	2-3	<5	0,25	<2 |	Слабое
II	3-4	5-15	0,25-0,75	2-3	Умеренное
III	4	15-25	0,75-1,25	3-4	Значительное
IV	5	25-40	1,25-2,0	4-5	Значительное
V	5-6	40-75	2,0-3,5	5-7	Сильное
VI	6-7	75-125	3,5-6,0	7-9	Сильное
VII	7-8	125-170	6,0-8,5	9-11	Очень сильное
VIII	8-9	170-220	8,5-11,0	11-12	Очень сильное
IX	10-12	>220	>11,0	>12	Исключительное

Спектральный метод

Статистический метод не дает всех необходимых данных для описания волнения как непрерывного случайного процесса. Более удобен для этих целей спектральный метод, который основан на представлении реального волнения в виде суммы бесконечного числа единичных волн со случайными амплитудами, частотами и фазами, т.е.

(2.26)

Погонная энергия каждой отдельно взятой волны в соответствии с (2.19) будет равна:

.

В то же время ее можно представить в виде

где -удельная энергия, приходящаяся на интервал при частоте

Приравнивая (2.27) и (2.28), получим

Отсюда

(2.30),

Зависимость (рис. 2.3) можно представить в виде графика спектральной плотности, или энергетического спектра. Он характеризует распределение энергии волн по амплитудам и частотам.

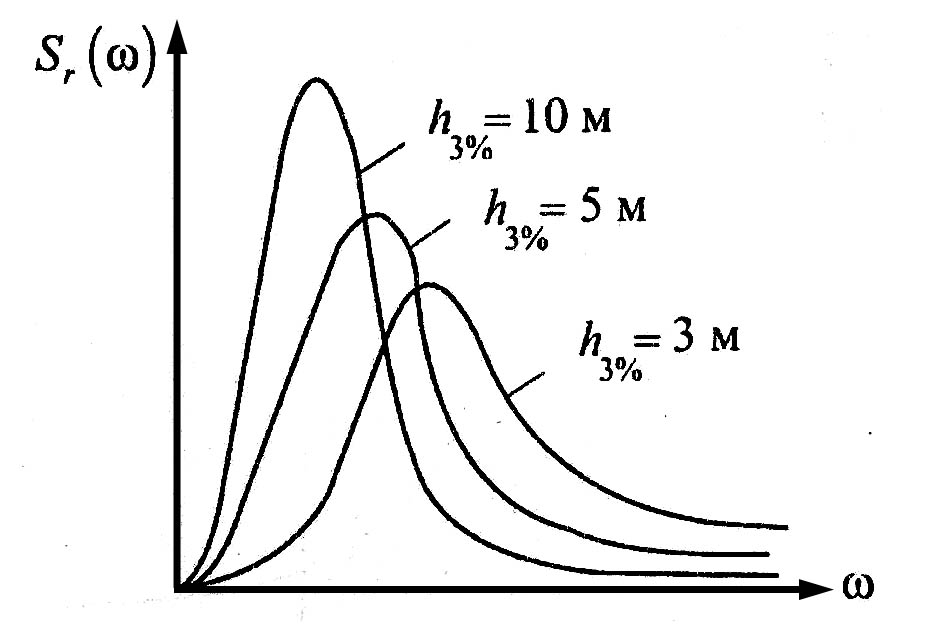
Рис. 2.3. Спектры нерегулярного волнения различной балльности

Связь между спектральными и статистическими характеристиками можно найти из выражения (2.21), подставив в него (2.29):

При , а сумма становится интегралом.

Тогда получим

С помощью дисперсии легко установить связь с высотой волны заданной обеспеченности и с соответствующими баллами волнения. Спектры чаще всего представляются в форме

(2.33)

где А, В, k, п - параметры, зависящие от условий волнообразования, от степени развитости волнения, от балльности, от акватории и т.д.

Обычно спектры нормируют (обезразмеривают), разделив 5'г(к>) на D и умножив на среднюю частоту :

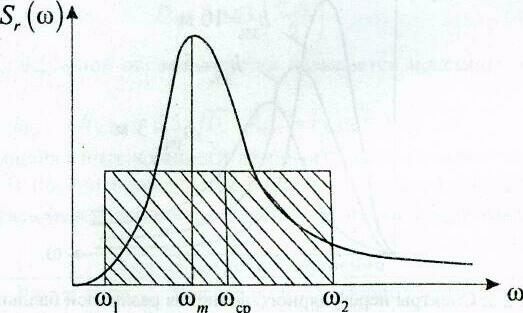
Рис. 9.4. Определение средней частоты спектра

где - нормированный спектр; - безразмерная частота. Удобство нормированных спектров в том, что они не зависят от балльности волнения.

Среднюю частоту можно определить из выражения

(2.35)

Приближенно можно определить графически в соответствии с рис. 2.4, при этом

где и определяются как границы прямоугольника, у которого площадь равна площади под кривой спектральной плотности, а момент инерции площади относительно оси ординат равен моменту инерции площади под кривой.

Дисперсия при нормировании определяется по формуле (2.24).

Существует статистическая связь между и . Для наиболее употребительных спектров

(2.36)

Окончательно в нормированном виде спектральная плотность записывается как

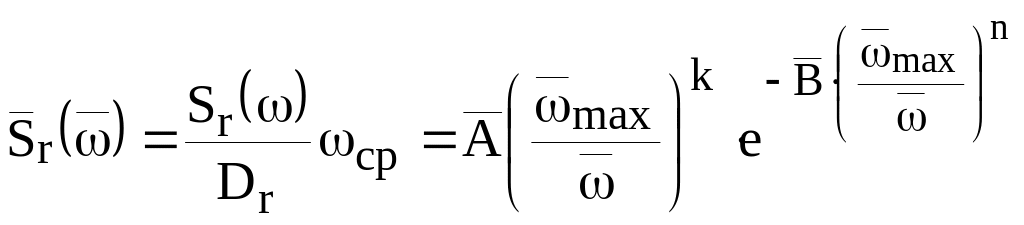(2.37)

где ; - частота, соответствующая максимуму спектра (см. рис. 2.4);

,

Величина связана с соотношением, зависящим от вида конкретного спектра.

02.07.2025