1.6.2 Гистограмма и плотность вероятности

В случае группировки данных, если n увеличивать и длины интервалов группировки умень-шать, то гистограмма и полигон неограниченно приближаются (в каждой точке сходятся по веро-ятности) к кривой плотности вероятности случайной величины.

Действительно, при построении гистограммы будем строить прямоугольники с высотой m_i/d_in, где d_i – длина интервала I_i. Вспомним, что для непрерывно распределенной случайной величины x вероятность попасть в интервал (а,b) вычисляется по формуле:

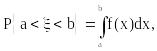
где f(x) – плотность распределения вероятностей величины Следовательно, вероятность попасть в интервал [x,x+x) выражается через плотность f(x), если длина интервала x мала, следующим образом:

Из этой формулы видно, что плотность вероятности – это вероятность, “приходящаяся в данной точке на единицу измерения”. Если эмпирическая вероятность попасть в i-ый интервал равна m_i/n, а d_i – это длина i-ого интервала, то эмпирическая вероятность, приходящаяся на единицу измерения, равна m_i/d_in. Если строить прямоугольники с такими высотами, то суммарная площадь всех прямоугольников равна 1. Так, построенная гистограмма изображает эмпирическую плотность. При n, стремящемся к бесконечности, она в каждой точке сходится по вероятности к теоретической плотности.

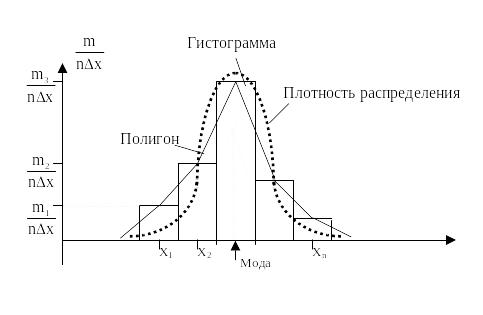
Рисунок 1.5

По виду построенной нами гистограммы (см. рисунок 1.5) можно предположить, что она построена по выборке из нормального распределения.

Приведенная ниже гистограмма дает основание полагать, что выборка получена из равномерного распределения (рисунок 1.6).

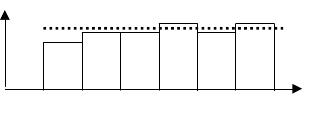
Рисунок 1.6

На рисунок 1.7 приведена еще одна гистограмма – не из нормального и не из равномерного распределения. По ее виду можно предположить, что выборка сделана из показательного распределения.

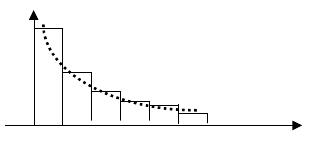
Рисунок 1.7

Эти примеры демонстрируют, как по гистограмме, построенной по выборке, можно примерно оценить тип распределения вероятностей. В дальнейшем мы научимся более точно решать задачу проверки по выборке гипотезы о генеральном распределении.

1.6.3 Кумулята, эмпирическая и теоретическая функции распределения

По выборочным данным можно вычислить эмпирическую вероятность события ( < x) для любого x (она равна (x)/n, где (x) – число вариант, меньших x) – т.е. найти эмпирическую функцию распределения. Введенные нами ранее “накопленные частоты” – это и есть значения эмпирической функции распределения в концах интервалов группировки, кумулята – ее сгла-женное графическое изображение.

Можно показать, что кумулята в каждой точке сходится по вероятности к теоретической функции распределения.

Остается добавить, что вследствие той же теоремы Бернулли числовые характеристики эмпирического распределения (математическое ожидание, дисперсия, мода, медиана и многие другие) в широком классе случаев также сходятся по вероятности к соответствующим характеристикам генерального распределения.

Таким образом, теорема Бернулли дает теоретическое обоснование для основной рекомендации, которую предлагает математическая статистика, – надо составить описание выборки, вычислить ее параметры и приписать свойства выборки всей совокупности, а параметрами, вычисленными по выборке, оценить параметры всей генеральной совокупности. При большом объеме выборки ошибка будет небольшой. В силу того, что изучается объект, в природу которого заложен элемент случайности, все оценки, вычисляемые по выборке, являются случайными значениями. Две разные выборки, полученные из одной и той же генеральной совокупности, дадут разные статистические таблицы, будут иметь разные средние значения, разные дисперсии и т.д. И хотя возможны выборки, которые на самом деле дают существенное отличие от теоретического распределения, с ростом объема выборки процент таких “плохих” выборок стремится к нулю. Кроме теоретического обоснования, что такой подход возможен, необходимо получить представление о точности и надежности эмпирической оценки. Это и будет предметом нашего рассмотрения.

Таким образом, первая задача, которую мы будем решать, – это задача построения оценок для параметров генеральной совокупности по данным выборки и изучение их точности и надежности. То есть мы считаем, что известен вид теоретического (генерального) распределения, но не известны и подлежат оценке параметры этого распределения. Так, например, для биномиального распределения по результатам n раз проведенного эксперимента надо оценить значение p. Или известно, что интересующая нас величина распределена нормально, над ней n раз проводятся испытания; по результатам испытаний надо построить оценки для ее математического ожидания и среднеквадратического отклонения (или дисперсии). Вспомним, что нормальное распределение целиком определяется двумя параметрами – математическим ожиданием и дисперсией. Нормаль-ное распределение является одним из самых распространенных распределений вероятности. Следовательно, данная задача охватывает очень большой круг приложений. Эта же методика позволит решить и задачу сравнения 2-х выборок. Например, сделать вывод о совпадении или различии средних значений их распределений. Эту задачу надо решить, например, в таких ситуациях, как: “внесены исправления в статью закона, повлияло ли это на среднее количество преступлений по этой статье?”, или “изменился режим работы, повлияло ли это на произво-дительность труда?” и т.д.